🔥 Turbine seus estudos com 47% OFF
no Toda Matéria+

Turbine seus estudos com 47% OFF no Toda Matéria+

Área do Losango: fórmula, exemplo e exercícios

Rosimar Gouveia

Professora de Matemática e Física

Para calcular a área do losango utilizamos as medidas das duas diagonais. A área do losango é determinada pela multiplicação das medidas de suas diagonais, dividindo o resultado por dois.

O losango é um polígono, uma figura geométrica plana de quatro lados iguais, ou seja, um quadrilátero equilátero.

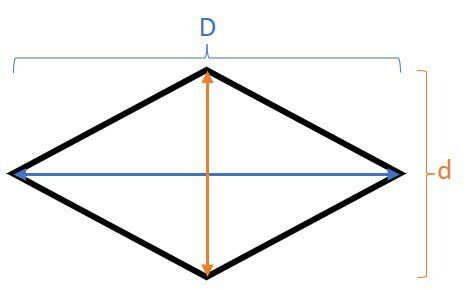
losango

Fórmula da área do losango

A fórmula para encontrar a área do losango é representada da seguinte maneira:

$começar estilo tamanho matemático 22px reto A igual a numerador reto D espaço. espaço reto d sobre denominador 2 fim da fração fim do estilo$

Sendo:
A: a área do losango
D: a diagonal maior
d: a diagonal menor

Exemplo do cálculo da área do losango:
Um losango possui sua diagonal maior com 24 cm e a menor 18 cm. Determine a área deste losango.

Resolução
Substituindo os valores na fórmula:

$começar estilo tamanho matemático 16px reto A igual a numerador reto D espaço. espaço reto d sobre denominador 2 fim da fração reto A igual a numerador 24 espaço. espaço 18 sobre denominador 2 fim da fração reto A igual a 432 sobre 2 reto A igual a 216 espaço cm ao quadrado fim do estilo$

Importante destacar que todo losango é um paralelogramo cujos lados opostos são iguais e paralelos. Possui também duas diagonais que se cruzam perpendicularmente.

Remover anúncios

Diferente do quadrado, que possui quatro ângulos iguais a 90°, o losango possui dois ângulos agudos (menores que 90º) e dois ângulos obtusos (maiores que 90º).

Enquanto o losango é um paralelogramo composto de quatro lados congruentes, o retângulo é um paralelogramo composto de quatro ângulos congruentes. Já o quadrado, é um paralelogramo composto de quatro lados e quatro ângulos congruentes.

Exercícios sobre área do losango

Exercício 1

Qual a área de um losango que possui diagonal maior medindo 10 cm e diagonal menor medindo 7 cm?

Remover anúncios

Ver Resposta

Portanto, a área do losango é 35 cm².

Exercício 2

Em um losango de diagonal maior com 40 cm, sua área é de 600 cm². Determine a medida de sua diagonal menor.

Ver Resposta

Substituindo os valores na fórmula da área do losango:

$reto A igual a numerador reto D espaço. espaço reto d sobre denominador 2 fim da fração 600 igual a numerador 40 espaço. espaço reto d sobre denominador 2 fim da fração$

Isolando d e resolvendo:

$600 igual a numerador 40 espaço. espaço reto d sobre denominador 2 fim da fração 600 espaço. espaço 2 espaço igual a espaço 40 espaço. espaço reto d numerador 600 espaço. espaço 2 sobre denominador 40 fim da fração igual a reto d 1200 sobre 40 igual a reto d 30 igual a reto d$

Remover anúncios

Exercício 3

Em um losango de área de 864 cm², sua diagonal menor mede 36 cm. Determine a medida dos lados deste losango.

Ver Resposta

Cálculo da diagonal maior.

$reto A igual a numerador reto D espaço. espaço reto d sobre denominador 2 fim da fração numerador reto A espaço. espaço 2 sobre denominador reto d fim da fração igual a reto D numerador 864 espaço. espaço 2 sobre denominador 36 fim da fração igual a reto D 48 igual a reto D$

Cálculo da medida do lado:

A metade de cada diagonal forma com um lado um triângulo retângulo de hipotenusa L.

Aplicando o Teorema de Pitágoras:

$reto L ao quadrado igual a abre parênteses reto D sobre 2 fecha parênteses ao quadrado mais abre parênteses reto d sobre 2 fecha parênteses ao quadrado$

$reto L ao quadrado igual a abre parênteses 48 sobre 2 fecha parênteses ao quadrado mais abre parênteses 36 sobre 2 fecha parênteses ao quadrado reto L ao quadrado igual a abre parênteses 24 fecha parênteses ao quadrado mais abre parênteses 18 fecha parênteses ao quadrado reto L ao quadrado igual a 576 espaço mais espaço 324 reto L ao quadrado igual a 900 reto L igual a raiz quadrada de 900 reto L igual a 30 espaço$

Assim, a medida dos lados do losango é 30 cm.

Remover anúncios

Continue praticando com exercícios sobre área do losango (com gabarito explicado).

Curiosidades

Há controvérsias sobre a origem da palavra losango, pois do latim "lausa" significa "pedra achatada" e do francês "losenge" designa "pedaço de bolo de ervas".
Os romanos chamavam o peixe arraia de "lausange".

Quer saber mais sobre as áreas de figuras planas? Leia também:

Área do trapézio

Área do triângulo

Área do retângulo

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.

Remover anúncios