Área do Paralelogramo: fórmula, como calcular e exemplo

Rafael C. Asth

Professor de Matemática e Física

A área do paralelogramo está relacionada com a medida da superfície dessa figura plana.

O paralelogramo é um polígono (figura plana e fechada) que possui quatro ângulos internos e quatro externos. A soma dos ângulos internos ou externos são de 360°.

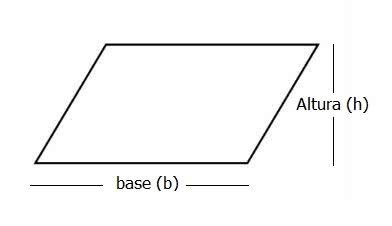
Área do Paralelogramo

Lembre-se que o paralelogramo é um quadrilátero que possui quatro lados opostos congruentes (mesma medida). Nessa figura, os lados opostos são paralelos.

Fórmula da área do paralelogramo

Para calcular a medida da área do paralelogramo multiplica-se o valor da base (b) pela altura (h). Logo, a fórmula é:

$começar estilo tamanho matemático 22px reto A igual a reto b sinal de multiplicação reto h fim do estilo$

Toda medida de área é em unidade quadradas.

Exemplo de cálculo da área de um paralelogramo:

Um terreno será usado para o plantio de hortaliças Ele possui frente de 250 m e um limite ao fundo de mesma medida, sendo paralela à frente.

Suas laterais, de mesma medida, possuem uma inclinação, formando um paralelogramo.

Para conhecer a área disponível para o plantio, traçou-se uma medida perpendicular em relação à frente e ao fundo, com 80 m.

Sendo 1 ha = 10 000 m² , quantos hectares há disponíveis para o plantio?

Resolução

Como se trata de um paralelogramo, para calcular sua área, faremos:

$reto A igual a reto b sinal de multiplicação reto h reto A igual a 250 espaço reto m sinal de multiplicação 80 espaço reto m reto A igual a 20 espaço 000 espaço reto m ao quadrado$

Para responder em ha, basta dividir por 10 000.

$reto A espaço igual a espaço 20 espaço 000 espaço reto m ao quadrado espaço dividido por espaço 10 espaço 000 espaço igual a espaço 2 espaço ha$

Assim, a área para plantio são de 2 ha (hectares)

Complemente sua pesquisa com a leitura dos artigos:

Você Sabia?

Os paralelogramos são definidos como quadriláteros de lados opostos paralelos. Assim, o quadrado, o retângulo e o losango são também paralelogramos.

Veja também os artigos sobre áreas de figuras planas:

Exercícios sobre área do paralelogramo

Exercício 1

Calcule a área de um paralelogramo com altura de 28 cm e base de 12 cm.

Ver Resposta

A = b.h
A = 12 . 28
A = 336 cm²

Exercício 2

Se um paralelogramo possui dois ângulos internos de 45°. Qual será o valor dos outros dois?

a) 45° e 90°
b) 120° e 45°
c) 130° e 140°
d) 136° e 240°
e) 90° e 75°

Ver Resposta

Alternativa c

Se a soma dos ângulos internos de um paralelogramo é de 360 °, para obter a resposta devemos somar os ângulos (além dos 90 já indicados no enunciado).

Exercício 3

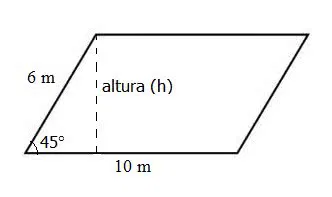
Calcule a área de um paralelogramo donde dois lados consecutivos tem medidas de 6 m e 10 m respectivamente, e ainda, formam um ângulo de 45°.

Ver Resposta

Como não temos a medida da altura, temos que primeiramente encontrar esse valor.

Assim, segundo a figura, quando traçamos a altura ela forma um triângulo retângulo com um ângulo reto de 90°.

Lembre-se que o triângulo retângulo é formado pela hipotenusa (lado oposto ao ângulo reto) e dois catetos (oposto e o adjacente). Aqui, temos que usar o valor do seno, cosseno ou tangente do ângulo de 45°.

No entanto, temos que lembrar que o seno é cateto oposto/ hipotenusa; o cosseno é cateto adjacente/ hipotenusa; e a tangente é cateto oposto/cateto adjacente. Sendo assim, pela figura utilizamos o valor de seno de 45°.

Logo:

Sem 45° = √2/2 = h/6
h = 3√2

Após descobrir o valor da altura podemos calcular a área do paralelogramo:

A = b . h
A = 10. 3√2
A = 30√2 m²

Saiba mais sobre o tema:

Fique Atento!

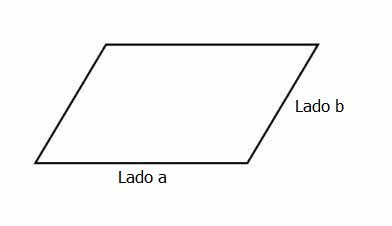
O perímetro de uma figura plana, diferente de sua área, corresponde a soma de todas as medidas dos lados. Portanto, no caso do paralelogramo o perímetro é dado pela fórmula:

$começar estilo tamanho matemático 20px reto P igual a 2 reto a mais 2 reto b fim do estilo$

$começar estilo tamanho matemático 20px reto P igual a 2 parêntese esquerdo reto a mais reto b parêntese direito fim do estilo$

Onde,

P: perímetro
a e b: comprimentos dos lados

Observação!

O valor da área é geralmente dado em cm² (centímetro quadrado), m² (metro quadrado) ou km² (quilômetro quadrado).

Já o perímetro sempre será a unidade de medida linear, ou seja, é dado em cm (centímetro), m (metro) ou km (quilômetro). Isso porque para encontrarmos a área multiplica-se os valores e para o perímetro soma-se os valores.