Área do setor circular: fórmulas, exemplos e exercícios
Um setor circular é a porção de um círculo delimitada por dois raios e o arco correspondente. É como uma "fatia" de pizza ou um pedaço de torta.
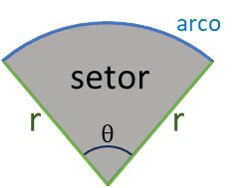
Os componentes do setor circular são:
- Raio (r): distância do centro do círculo até qualquer ponto da borda.
- Ângulo: formado pelos dois raios que delimitam o setor. Pode ser medido em graus ou radianos.
- Arco: parte da circunferência entre os dois raios.
Fórmulas para calcular a área do setor circular
Para determinar a medida da área ocupada por um setor circular são necessárias as da medida do raio e do ângulo central, formado pelos raios.
Uma vez que o ângulo pode ser medida tanto em graus como em radianos, a fórmula para seu cálculo pode assumir as duas formas.
Fórmula em Graus
Para um setor circular com ângulo θ em graus:
Onde:
θ é a medida do ângulo em graus;
r é a medida o raio;
é um número constante. Aproximadamente 3,1415 …
Repare que é uma divisão entre a parte (medida do ângulo que determina o setor) e o todo (360º, ângulo que determina o próprio círculo).
Exemplo
Calcule a área de um setor circular com raio de 5 cm e ângulo de 60°.
Aproximando , temos:
Fórmula em Radianos
Para um setor circular com ângulo θ em radianos a fórmula é bem semelhante. Lembremos que o ângulo central de 360° que determina o círculo, em radianos, equivale a .
Substituir o 360° por é a única alteração necessária e, a fórmula como apresentada acima já é suficiente para o cálculo da área do setor circular. No entanto, ela pode ser simplificada cancelando os números
, ficando assim:
Exemplo
Calcule a área de um setor circular com raio de 4 cm e ângulo de radianos.
Aproximando , temos:
Veja mais sobre radiano.
Exercícios sobre área do setor circular
Exercício 1
Uma praça tem uma fonte em forma de setor circular com um ângulo central de 90º e um raio de 10 metros. A equipe de manutenção precisa calcular a área da fonte para planejar a limpeza.
Qual é a área do setor circular? (Use π≈3,14)
A) 15,7 m²
B) 31,4 m²
C) 78,5 m²
D) 157 m²
E) 78,85 m²
Os dados fornecidos são:
Ângulo central = 90º;
raio = 10 metros.
Cálculo
Substituindo os valores na fórmula, temos:
Logo, a área é de 78,5 m².
Exercício 2
Uma empresa deseja construir um jardim em forma de setor circular em um parque. O ângulo central do setor é de rad e o raio do setor circular é de 15 metros. A empresa precisa calcular a área do setor para determinar a quantidade de grama necessária para cobrir o jardim.
Qual é a área do setor circular? (Use π≈3,14)
A) 117,75 m²
B) 235,5 m²
C) 94,2 m²
D) 78,5 m²
E) 188,4 m²
Os dados fornecidos são:
Ângulo central de rad;
raio de 15 metros.
Cálculo da área:
Utilizamos a fórmula simplificada:
Logo, a área é de aproximadamente 117,75 m².
Exercício 3
O proprietário de um parque aquático deseja construir uma piscina em suas dependências. A figura representa a vista superior dessa piscina, que é formada por três setores circulares idênticos, com ângulo central igual a 60°. O raio R deve ser um número natural.
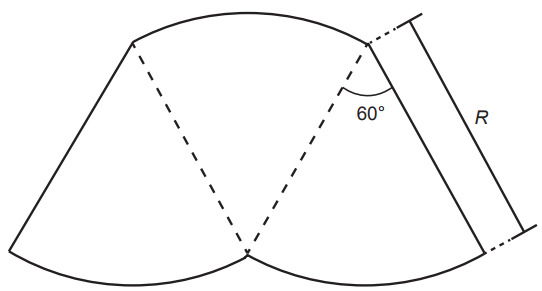
O parque aquático já conta com uma piscina em formato retangular com dimensões 50 m x 24 m.
O proprietário quer que a área ocupada pela nova piscina seja menor que a ocupada pela piscina já existente.
Considere 3,0 como aproximação para π
O maior valor possível para R, em metros, deverá ser
a) 16.
b) 28.
c) 29.
d) 31.
e) 49.
Cálculo da área já existente
Como o formato é retangular, a área é calculada por:
A = 50 m x 24 m = 1200 m²
Cálculo da nova área
Para um setor circular, a área é determinada como:
A imagem ilustra três setores circulares, por isso multiplicaremos por três. Também considera e o ângulo central de 60º.
Substituindo na fórmula acima e fazendo simplificações:
A área determinada por esta expressão deve ser menor que 50 x 24, logo:
Resolvendo a inequação para r, temos:
Como:
30 x 30 = 900
29 x 29 = 841
28 x 28 = 784
Por tentativa e erro, o raio deve ser 28, pois o enunciado o restringe à um número natural.
Aprenda mais com:
- Como Calcular a Área do Círculo?
- Circunferência: diâmetro, comprimento, fórmulas e exercícios
- Áreas de Figuras Planas
Pratique mais com exercícios de circunferência e círculo com respostas.
ASTH, Rafael. Área do setor circular: fórmulas, exemplos e exercícios. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/area-do-setor-circular/. Acesso em:


