Área e Perímetro: fórmulas, exemplos e exercícios

Rafael C. Asth

Professor de Matemática e Física

Na geometria, os conceitos de área e perímetro são utilizados para determinar as medidas de alguma figura.

Veja abaixo o significado de cada conceito:

Área: equivale à medida da superfície de uma figura geométrica.
Perímetro: soma das medidas de todos os lados de uma figura.

Geralmente, para encontrar a área de uma figura, realizam-se cálculos com as medidas destas figuras. Já o perímetro é a soma dos segmentos de retas que formam a figura, chamados de lados (l).

Para encontrar esses valores é importante analisar a forma da figura. Assim, se vamos encontrar o perímetro de um triângulo, somamos as medidas dos três lados. Se a figura for um quadrado somamos as medidas dos quatro lados.

Saiba mais sobre as figuras geométricas:

• Geometria Plana
• Geometria Espacial

Áreas e Perímetros de Figuras Planas

Confira abaixo as fórmulas para encontrar a área e o perímetro de algumas figuras planas.

Triângulo:

O triângulo é uma figura fechada e plana formado por três lados.

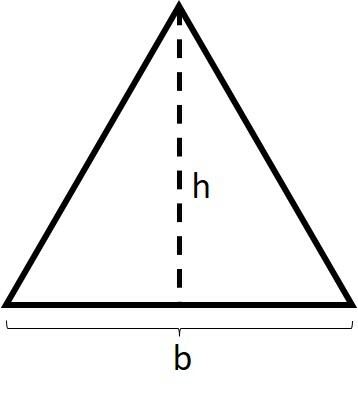
Fórmula da área do triângulo:

Onde b é a medida da base e h da altura.

Fórmula do perímetro do triângulo:

Onde a, b e c são as medidas dos lados.

Exemplo:
Em um triângulo isósceles com lados iguais a 6, 5 e 5 cm, sua altura é de 8 cm. Determine sua área e perímetro.

Resolução

Cálculo da área:

Cálculo do perímetro:

P = 6 + 5 + 5 = 16 cm

Que tal ler mais sobre os triângulos? Veja mais em Classificação dos Triângulos.

Retângulo

O retângulo é uma figura fechada e plana formada por quatro lados. Os retângulos são formados por dois pares de lados congruentes e paralelos.

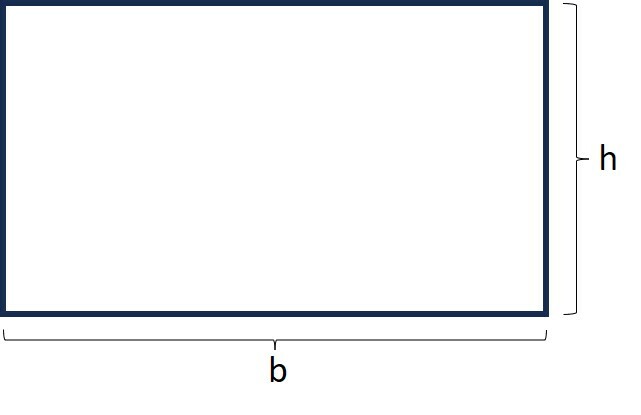
Fórmula da área do retângulo:

Onde b é a medida da base e h da altura.

Fórmula do perímetro do retângulo:

Exemplo:

Em um retângulo a base mede 5 cm e a altura 3 cm. Determine a área e o perímetro.

Resolução:

Cálculo da área:

A = b . h = 5 . 3 = 15 cm²

Cálculo do perímetro:

P = 5 + 3 + 5 + 3 = 16 cm

Veja também: Retângulo.

Quadrado

É uma figura fechada e plana formada por quatro lados e ângulos congruentes (possuem a mesma medida).

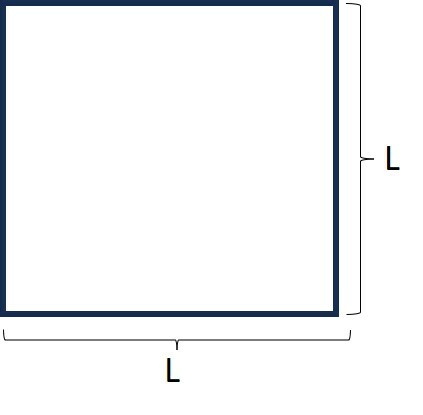
Fórmula da área do quadrado:

Fórmula do perímetro do quadrado:

Exemplo
Em um quadrado de lado de 7 cm, calcule a área e o perímetro.

Resolução:

Cálculo da área:

A = L² = 7² = 49 cm²

Cálculo do perímetro:

P = 4L = 4 . 7 = 28 cm

Círculo

É figura plana e fechada, limitada por uma linha curva chamada de circunferência.

Fórmula da área do círculo:

Fórmula do perímetro do círculo:

Onde r é a medida do raio.

Exemplo
Em um círculo de raio de 10 cm, determine a área e o perímetro.

Resolução:

Cálculo da área:

Cálculo do perímetro:

Atenção!

π: constante de valor aproximado de 3,14.
r: raio (distância entre o centro e a extremidade).

Trapézio

O trapézio é uma figura plana e fechada que possui dois lados (bases) paralelos, onde uma é maior e outra menor.

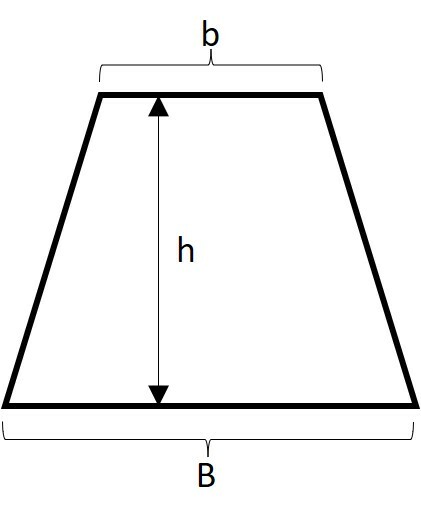
Fórmula da área do trapézio:

Exemplo
Determine a área de um trapézio com bases de 7 cm e 10 cm, cuja altura é de 8 cm.

Resolução:

Veja mais sobre o Trapézio.

Losango

O losango é figura plana e fechada composta de quatro lados iguais. Essa figura apresenta lados e ângulos opostos congruentes e paralelos.

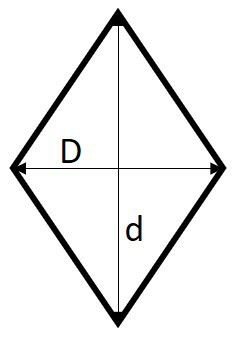
Fórmula da área do losango:

Onde D é diagonal maior e d é a menor.

Fórmula do perímetro do losango:

Exemplo
Um losango possui diagonais de 8 cm e 6 cm. Seus lados medem 5 cm. Determine área e perímetro.

Resolução

Cálculo da área:

Cálculo do perímetro.

P = 4L = 4 . 5 = 20 cm

Saiba mais sobre as área e perímetros das figuras:

• Área dos Polígonos
• Área do Triângulo
• Área do Losango
• Área do Círculo
• Área do Trapézio
• Área do Retângulo
• Área do Quadrado
• Área do Hexágono
• Perímetro do Retângulo
• Perímetros de Figuras Planas
• Áreas de Figuras Planas
• Área de Figuras Planas - Exercícios

Exercícios sobre área e perímetro

Exercício 1

Calcule as áreas das figuras abaixo:

a) Triângulo de base 5 cm e altura de 12 cm.

b) Retângulo de base 15 cm e altura de 10 cm.

c) Quadrado com lado de 19 cm.

d) Círculo com diâmetro de 14 cm.

e) Trapézio com base menor de 5 cm, base maior de 20 cm e altura de 12 cm.

f) Losango com diagonal menor de 9 cm e diagonal maior de 16 cm.

Exercício 2

Calcule os perímetros das figuras abaixo:

a) Triângulo isósceles com dois lados de 5 cm e outro de 3 cm.

b) Retângulo de base 30 cm e altura de 18 cm.

c) Quadrado de lado 50 cm.

d) Círculo com raio de 14 cm.

e) Trapézio de base maior 27 cm, base menor de 13 cm e lados de 19 cm.

f) Losango com lados de 11 cm.

Confira mais questões, com resolução comentada, em Exercícios sobre Área e Perímetro.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.