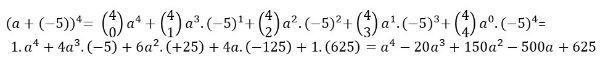Binômio de Newton: fórmula e como calcular (com exemplos)
O Binômio de Newton refere-se a potência na forma (x + y)n , onde x e y são números reais e n é um número natural.
O desenvolvimento do binômio de Newton em alguns casos é bastante simples. Podendo ser feita multiplicando-se diretamente todos os termos.
Contudo, nem sempre é conveniente utilizar esse método, pois conforme o expoente, os cálculos ficarão extremamente trabalhosos.
Para facilitar a expansão de potência do tipo (x + y)n
Especialmente com grandes expoentes (n com alto valor) utilizamos o procedimento Binômio de Newton. Trata-se de uma série de operações, guiadas por uma fórmula, que simplificam os cálculos.
Exemplo
Represente a forma expandida do binômio (4 + y)2:
Como o expoente do binômio é 2, um modo expandir a potência é usar a propriedade multiplicativa.
Esta técnica se torna inviável para calcular algo como (4 + y)9. Para solucionar problemas deste tipo, utilizaremos o Binômio de Newton, um método desenvolvido pelo inglês Isaac Newton (1643-1727) aplicado em cálculos de probabilidades e estatísticas.
Fórmula do Binômio de Newton
O binômio de Newton é um método simples que permite determinar a enésima potência de um binômio.
Esse método foi desenvolvido pelo inglês Isaac Newton (1643-1727) e é aplicado em cálculos de probabilidades e estatísticas.
A fórmula do binômio de Newton podendo ser escrita como:
![]()
Analisemos por partes.
Os coeficientes binomiais
As colunas com dois termos entre parenteses são os coeficientes dos termos da expansão. Ou seja, são os valores numéricos que multiplicam cada termo.
Repare que o número de cima é sempre o mesmo. Ele é o expoente da potência. Já o número de baixo segue uma ordem crescente a cada termo, que vai de 0 até o próprio n.
Estes valores são calculados como uma combinação simples, usando a fórmula:
![]()
n! : fatorial de n. É calculado como n = n (n - 1)(n - 2) . ... . 3 . 2 . 1
p! : fatorial de p
(n - p)! : fatorial de (n - p)
A quantidade de termos na expansão do binômio de Newton é, portanto, sempre um termo a mais que o expoente.
Quantidade de termos = n + 1
Isto se deve por sempre começarmos do 0 e ir até o próprio n.
Exemplo
Calculemos o número binomial .
Os termos algébricos
Os termos algébricos são as letras, quando existem. Para escrevê-los você irá usar a regra prática:
1. Escreva uma multiplicação entre os elementos do binômio, para cada termo (número binomial).
2. Da esquerda para direita, os expoentes do primeiro elemento seguem ordem decrescente, de n até 0.
3. Da esquerda para direita, os expoentes do segundo elemento seguem ordem crescente, de 0 até n.
4. Simplifique os expoentes iguais a 0, pois potências com expoente 0 sempre resultam em 1.
5. Caso necessário, multiplique coeficientes remanescentes.
Exemplo
Efetuar o desenvolvimento de (x + y)5:
Primeiro escrevemos a fórmula do binômio de Newton
![]()
Agora, devemos calcular os números binomiais para encontrar o coeficiente de todos os termos.
Considera-se que 0! = 1

Assim, o desenvolvimento do binômio é dado por:
(x + y)5 = x5 + 5x4y + 10 x3y2 + 10x2y3 + 5xy4 + y5
Termo Geral do Binômio de Newton
O termo geral do binômio de Newton é dado por:
![]()
Exemplo
Qual é o 5º termo do desenvolvimento de (x + 2)5, conforme as potências decrescentes de x?
Como queremos T5 (5º termo), então 5 = k +1 ⇒ k = 4.
Substituindo os valores no temos geral, temos:
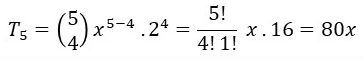
Binômio de Newton e Triângulo de Pascal
O triângulo de Pascal é um triângulo numérico infinito, formado por números binomiais.
O triângulo é construído colocando-se 1 nos lados. Os demais números são encontrados somando os dois números imediatamente acima deles.

Os coeficientes do desenvolvimento de um binômio de Newton podem ser definidos utilizando o triângulo de Pascal.
Desta maneira evitam-se os cálculos repetitivos dos números binomiais.
Exemplo
Determine o desenvolvimento do binômio (x + 2)6.
Primeiro é necessário identificar qual linha iremos usar para o binômio dado.
A primeira linha corresponde ao binômio do tipo (x + y)0, desta forma, usaremos a 7ª linha do triângulo de Pascal para o binômio de expoente 6.
(x + 2)6 = 1x6 + 6x5.21 + 15x4.22 + 20x3.23 + 15x2.24 + 6x1.25 + 1x0.26
Assim, o desenvolvimento do binômio ficará:
(x + 2)6= x6 + 12x5 + 60x4 + 160x3 + 240x2 + 192x + 64
Para saber mais, leia também:
Exercícios Resolvidos sobre Binômio de Newton
Exercício 1
Qual o desenvolvimento do binômio (a - 5)4 ?
Exercício 2
Qual é o termo médio (ou central) no desenvolvimento de (x - 2)6?
[LEITURA-RELACIONADA=4020 "Fórmulas de Matemática"
Você pode praticar mais com:
ASTH, Rafael. Binômio de Newton: fórmula e como calcular (com exemplos). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/binomio-de-newton/. Acesso em: