Bissetriz: o que é e como determinar

Rafael C. Asth

Professor de Matemática e Física

A bissetriz é uma semirreta interna a um ângulo, traçada a partir do seu vértice, que o divide em dois ângulos congruentes (ângulos com a mesma medida).

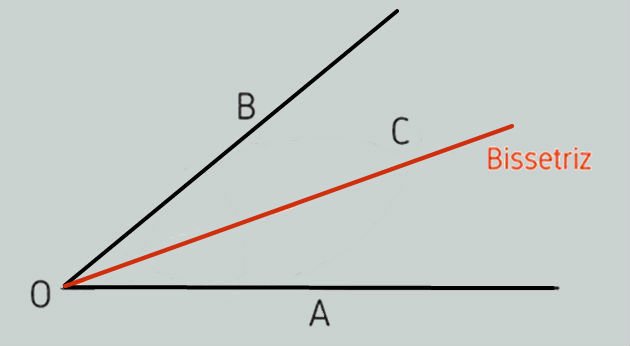
Na figura abaixo, a bissetriz, indicada por uma reta em vermelho, reparte o ângulo AÔB ao meio.

Assim, o ângulo AÔB fica dividido em dois outros ângulos, o AÔC e o BÔC, de mesmas medidas.

Por exemplo, se o ângulo AÔB medir 90°, os ângulos AÔC e BÔC passam a medir 45° cada, pois 90/2 = 45.

Como encontrar a bissetriz?

Se conhecermos o ângulo ao qual a bissetriz será traçada, basta dividi-lo por 2. Caso não conhecermos o valor deste ângulo, a bissetriz pode ser obtida com o auxílio de uma compasso.

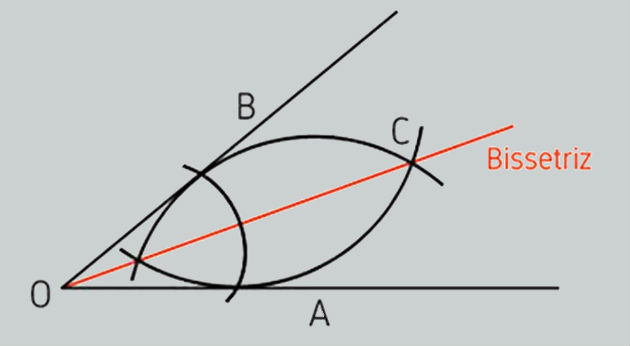
Para encontrar a bissetriz, basta seguir os seguintes passos utilizando o compasso:

1. abra um pouco o compasso e coloque a sua ponta seca no vértice do ângulo.
2. faça um traço de circunferência sobre as semirretas OA e OB.
3. com o compasso aberto, coloque a ponta seca no ponto de intersecção da semirreta OA e faça um traço de circunferência com o compasso virado para dentro do ângulo.
4. faça o mesmo, agora com a ponta seca no ponto de intersecção da semirreta OB.
5. trace uma semirreta do vértice do ângulo até o ponto de intersecção dos traços que acabou de fazer. A semirreta OC é a bissetriz.

Bissetriz dos ângulos de um triângulo

Os triângulos possuem ângulos internos e externos. Podemos traçar bissetrizes em cada um destes ângulos. O ponto de encontro das três bissetrizes internas de um triângulo é chamado de incentro.

O incentro está a mesma distância dos três lados do triângulo. Além disso, quando uma circunferência está inscrita em um triângulo, este ponto representa o centro da circunferência.

Teorema da Bissetriz Interna

A bissetriz interna de um triângulo divide o lado oposto em segmentos proporcionais aos lados adjacentes. Na imagem abaixo, a bissetriz do ângulo  divide o lado a em dois segmentos x e y.

A partir do teorema da bissetriz interna, podemos escrever a seguinte proporção, considerando o triângulo ABC da imagem:

Exemplo

Encontre o valor de x indicado no triângulo da figura abaixo, sabendo que representa a bissetriz do ângulo A.

Resolução

Como é a bissetriz interna do triângulo, então podemos aplicar o teorema. Sendo assim, temos a seguinte relação:

Substituindo os valores do problema, encontramos:

Teorema da Bissetriz Externa

Os ângulos externos de um triângulo são os ângulos adjacentes aos ângulos internos. Para encontrar esses ângulos, traçamos um prolongamento do lado adjacente.

Quando a bissetriz externa intercepta o prolongamento do lado oposto, formam segmentos proporcionais aos lados adjacentes, conforme figura abaixo:

Considerando o triângulo ABC da figura, conforme o teorema da bissetriz externa, podemos escrever a seguinte proporção:

Sendo,

x = a + y

Exemplo

No triângulo representado na figura abaixo, encontre o valor de x, considerando que a reta AD é uma bissetriz externa deste triângulo.

Resolução

Sendo a reta AD uma bissetriz externa, podemos aplicar o teorema da bissetriz externa para encontrar o valor de x. Teremos então a seguinte proporção:

Leia também:

• Teorema de Tales
• Mediatriz
• Teorema de Pitágoras

Exercícios sobre bissetriz

Exercício 1

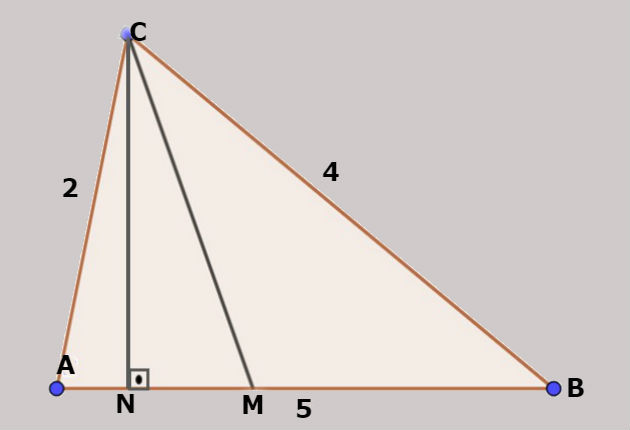
(Fuvest) Um triângulo ABC tem lados de comprimentos AB = 5, BC = 4 e AC = 2. Sejam M e N os pontos de AB tais que CM é a bissetriz relativa ao ângulo ACB e CN é a altura relativa ao lado AB. Determinar o comprimento de MN.

Exercício 2

(PUC-RJ) Considere um triângulo ABC retângulo em A onde AB = 21 e AC = 20. BD é a bissetriz do ângulo ABC. Quanto mede AD?

a) 42/5
b) 21/20
c) 20/21
d) 9
e) 8

Pratique também Teorema de Pitágoras - Exercícios.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.