Condição de existência de um triângulo (com exemplos)
A condição de existência de um triângulo é uma característica obrigatória nos comprimentos de seus três lados. Ela garante que a figura pode ser fechada, ou seja, que os lados se liguem por vértices.
Um triângulo é uma figura formada por três segmentos de reta, plana e, sobretudo, fechada. No entanto, nem todo trio de segmentos consegue fechar o triângulo.
Para três segmentos fecharem um triângulo, cada lado deve ser menor que a soma dos outros dois.
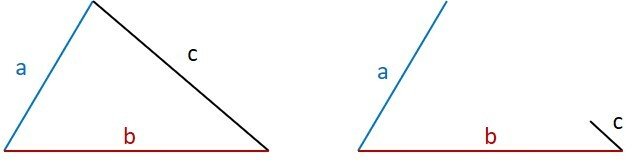
Três lados quaisquer, que chamaremos de a, b e c, para conseguirem formar um triângulo, as medidas devem obedecer:
As três condições devem ser satisfeitas. Caso uma falhar, não é possível fechar e formar o triângulo.
Exemplo 1
Verifique se três segmentos com 4 cm, 7 cm e 12 cm podem formar um triângulo.
- 4 < 7 + 12 (verdadeiro)
- 7 < 4 + 12 (verdadeiro)
- 12 < 4 + 7 (falso), pois 4 + 7 = 11 e 12 não é menor que 11.
Logo, não é possível formar um triângulo com os segmentos 4 cm, 7 cm e 12 cm.
Exemplo 2
Verifique se é possível formar um triângulo com segmentos de 5 cm, 9 cm e 10 cm.
- 5 < 9 + 10 (verdadeiro)
- 9 < 5 + 10 (verdadeiro)
- 10 < 5 + 9 (verdadeiro)
Desta forma, é possível formar um triângulo com os segmentos 5 cm, 9 cm e 10 cm.
Aprenda mais sobre triângulos em:
- Triângulo: tudo sobre este polígono
- Classificação dos Triângulos
- Exercícios sobre triângulos explicados
- Área do Triângulo: como calcular?
- Soma dos ângulos internos de um triângulo
Desativar verificaçãoSugestões Premium
ASTH, Rafael. Condição de existência de um triângulo (com exemplos). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/condicao-de-existencia-de-um-triangulo/. Acesso em:


