Dilatação Térmica: como calcular e exemplos

Rafael C. Asth

Professor de Matemática e Física

Dilatação Térmica é a variação que ocorre nas dimensões de um corpo quando submetido a uma variação de temperatura.

De uma maneira geral, os corpos, sejam eles: sólidos, líquidos ou gasosos, aumentam suas dimensões quando aumentam sua temperatura.

Esse fenômeno ocorre porque as partículas que compõem o material (átomos ou moléculas) tendem a vibrar mais rapidamente e ocupar mais espaço à medida que a temperatura aumenta.

Por outro lado, quando a temperatura diminui ocorre a contração térmica. Neste caso, as partículas vibram menos e se aproximam umas das outras, fazendo com que o material contraia.

Dilatação Térmica dos Sólidos

Um aumento de temperatura faz com que aumente a vibração e o distanciamento entre as moléculas e partículas que constituem um corpo sólido. Em consequência disso, ocorre um aumento nas suas dimensões.

Dependendo da dilatação mais significativa em uma determinada dimensão (comprimento, largura e profundidade), a dilatação dos sólidos é classificada em: linear, superficial e volumétrica.

Dilatação Linear

A dilatação linear considera a dilatação sofrida por um corpo apenas em uma das suas dimensões. É o que acontece, por exemplo, com um fio, em que o seu comprimento é mais relevante do que a sua espessura.

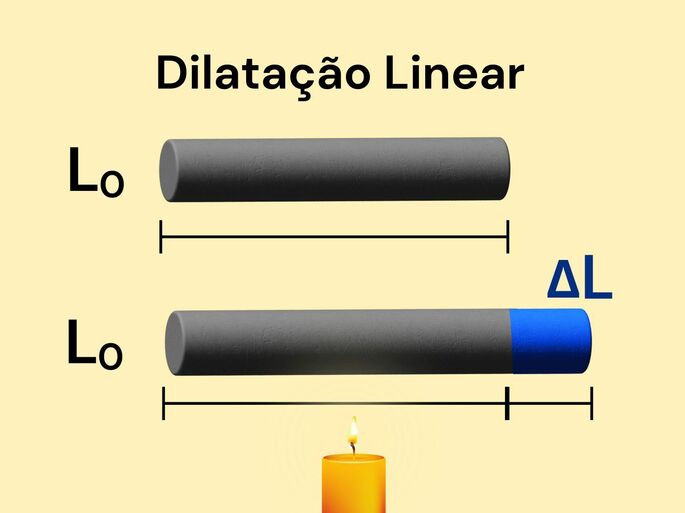
Para calcular a dilatação linear utilizamos a seguinte fórmula:

$começar estilo tamanho matemático 20px reto delta maiúsculo reto L igual a reto L com 0 subscrito. reto alfa. reto delta maiúsculo reto teta fim do estilo$

Onde,

ΔL: Variação do comprimento (m ou cm)
L₀_: Comprimento inicial (m ou cm)
α: Coeficiente de dilatação linear (ºC^-1)
Δθ: Variação de temperatura (ºC)

Exemplo de cálculo de dilatação térmica linear:

Um trilho de trem de 10 metros tem seu comprimento alterado devido à variação de 30 °C ao longo do dia. Possuindo um coeficiente de dilatação linear de $11 espaço sinal de multiplicação espaço 10 à potência de menos 6 fim do exponencial espaço º C à potência de menos 1 fim do exponencial$ , determine o comprimento final do trilho.

Resolução

Dados:

$reto L com 0 subscrito igual a 10 espaço reto m reto alfa espaço igual a espaço 11 espaço reto x espaço 10 à potência de menos 6 fim do exponencial espaço º reto C à potência de menos 1 fim do exponencial incremento reto teta igual a 30 º reto C$

Substituindo na fórmula da dilatação:

$reto delta maiúsculo reto L igual a reto L com 0 subscrito. reto alfa. reto delta maiúsculo reto teta reto delta maiúsculo reto L igual a 10 espaço. espaço 11 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço. espaço 30 reto delta maiúsculo reto L igual a 3300 espaço espaço. espaço 10 à potência de menos 6 fim do exponencial espaço reto delta maiúsculo reto L igual a 0 vírgula 0033 espaço reto m$

Assim, a variação no comprimento foi de 0,0033 m. Para determinar o comprimento final, basta adicionar o valor da dilatação ao comprimento inicial.

10 + 0,0033 = 10,0033 m

Solução
O comprimento final é de 10,0033 m.

Dilatação Superficial

A dilatação superficial considera a dilatação sofrida por uma determinada superfície. É o que acontece, por exemplo, com uma chapa de metal delgada.

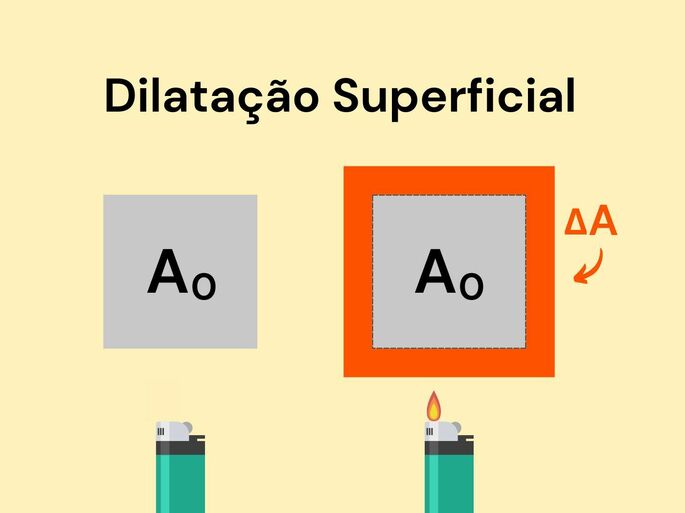
Para calcular a dilatação superficial utilizamos a seguinte fórmula:

$começar estilo tamanho matemático 20px reto delta maiúsculo reto A igual a reto A com 0 subscrito. reto beta. reto delta maiúsculo reto teta fim do estilo$

Onde,

ΔA: Variação da área (m² ou cm²)
A₀: Área inicial (m² ou cm²)
β: Coeficiente de dilatação superficial (ºC^-1)
Δθ: Variação de temperatura (ºC)

Importa destacar que o coeficiente de dilatação superficial (β) é igual a duas vezes o valor do coeficiente de dilatação linear (α), ou seja:

$começar estilo tamanho matemático 20px reto beta igual a 2. reto alfa fim do estilo$

Exemplo de cálculo de dilatação térmica superficial:

Uma chapa de cobre com área de 1 m², inicialmente à temperatura de 20 °C, é aquecida até 90 °C. Sendo o coeficiente de dilatação linear do cobre igual a $17.10 à potência de menos 6 fim do exponencial espaço º C à potência de menos 1 fim do exponencial espaço$ , determine a variação de sua área.

Resolução

Dados:

$reto A com 0 subscrito igual a 1 espaço reto m ao quadrado reto alfa igual a 17 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço º reto C incremento reto teta igual a reto teta com final subscrito espaço menos espaço reto teta com inicial subscrito igual a 90 espaço menos espaço 20 espaço igual a 70 º reto C$

Para o cálculo, precisamos determinar o coeficiente de dilatação superficial do cobre.

$começar estilo tamanho matemático 16px reto beta igual a 2. reto alfa reto beta igual a 2 espaço. espaço 17 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço º reto C à potência de menos 1 fim do exponencial reto beta igual a 34 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço º reto C à potência de menos 1 fim do exponencial fim do estilo$

Substituindo os valores na fórmula:

$começar estilo tamanho matemático 16px reto delta maiúsculo reto A igual a reto A com 0 subscrito. reto beta. reto delta maiúsculo reto teta reto delta maiúsculo reto A igual a 1 espaço. espaço 34 espaço. espaço 10 à potência de menos 6 fim do exponencial. espaço 70 reto delta maiúsculo reto A igual a 2 espaço 380 espaço. espaço 10 à potência de menos 6 fim do exponencial reto delta maiúsculo reto A igual a 0 vírgula 00238 espaço reto m ao quadrado fim do estilo$

Solução
A variação da área foi de 0,00238 m².

Dilatação Volumétrica

A dilatação volumétrica resulta do aumento no volume de um corpo, acontecendo, por exemplo, com uma barra de ouro.

Para calcular a dilatação volumétrica utilizamos a seguinte fórmula:

$começar estilo tamanho matemático 20px reto delta maiúsculo reto V igual a reto V com 0 subscrito. reto gama. reto delta maiúsculo reto teta fim do estilo$

Onde,

ΔV: Variação do volume (m³ ou cm³)
V₀: Volume inicial (m³ ou cm³)
γ: Coeficiente de dilatação volumétrica (ºC^-1)
Δθ: Variação de temperatura (ºC)

Repare que o coeficiente de dilatação volumétrico (γ) é três vezes maior que coeficiente de dilatação linear (α), ou seja:

$começar estilo tamanho matemático 20px reto gama igual a 3. reto alfa fim do estilo$

Exemplo de cálculo de dilatação térmica volumétrica:

Determine a variação no volume de uma barra de ouro de 0,002 m³, quando exposta a uma fonte de calor que altera dua temperatura de 25 °C até 120 °C. O coeficiente de dilatação linear do ouro é de $15 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço º reto C à potência de menos 1 fim do exponencial$ .

Resolução

Dados:

$reto V com 0 subscrito igual a 0 vírgula 002 espaço reto m ao cubo reto alfa igual a 15 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço º reto C à potência de menos 1 fim do exponencial incremento reto teta igual a 120 espaço menos espaço 25 espaço igual a 95 espaço º reto C$

Devemos determinar o coeficiente volumétrico do ouro.

$começar estilo tamanho matemático 16px reto gama igual a 3. reto alfa reto gama igual a 3 espaço. espaço 15 espaço. espaço 10 à potência de menos 6 fim do exponencial reto gama igual a 45 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço º reto C à potência de menos 1 fim do exponencial fim do estilo$

Substituindo os valores na fórmula:

$começar estilo tamanho matemático 16px reto delta maiúsculo reto V igual a reto V com 0 subscrito. reto gama. reto delta maiúsculo reto teta reto delta maiúsculo reto V igual a 0 vírgula 002 espaço. espaço 45 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço. espaço 95 reto delta maiúsculo reto V igual a 8 vírgula 55 espaço. espaço 10 à potência de menos 6 fim do exponencial reto delta maiúsculo reto V igual a 0 vírgula 00000855 espaço reto m fim do estilo$

Solução
A variação no volume da barra é de 0,00000855 m.

Coeficientes de Dilatação Linear

A dilatação sofrida por um corpo depende do material que o compõe. Desta forma, no cálculo da dilatação é considerado a substância de que o material é feito, através do coeficiente de dilatação linear (α).

A tabela abaixo indica os diferentes valores que podem assumir o coeficiente de dilatação linear para algumas substâncias:

Substância	Coeficiente de Dilatação Linear (ºC^-1)
Porcelana	3.10^-6
Vidro Comum	8.10^-6
Platina	9.10^-6
Aço	11.10^-6
Concreto	12.10^-6
Ferro	12.10^-6
Ouro	15.10^-6
Cobre	17.10^-6
Prata	19.10^-6
Alumínio	22.10^-6
Zinco	26.10^-6
Chumbo	27.10^-6

Dilatação Térmica dos Líquidos

Os líquidos, salvo algumas exceções, aumentam de volume quando a sua temperatura aumenta, da mesma forma que os sólidos.

Entretanto, devemos lembrar que os líquidos não apresentam forma própria, adquirindo a forma do recipiente que os contém.

Por isso, para os líquidos, não faz sentido calcularmos, nem a dilatação linear, nem a superficial, só a volumétrica.

Desta forma, apresentamos abaixo a tabela do coeficiente de dilatação volumétrico de algumas substâncias.

Líquidos	Coeficientes de Dilatação Volumétrico (ºC^-1)
Água	1,3.10^-4
Mercúrio	1,8.10^-4
Glicerina	4,9.10^-4
Álcool	11,2.10^-4
Acetona	14,93.10^-4

Quer saber mais? Leia também:

Exercícios de dilatação térmica

Exercício 1

Um fio de aço apresenta comprimento igual a 20 m quando sua temperatura é de 40 ºC. Qual será seu comprimento quando sua temperatura for igual a 100 ºC? Considere do coeficiente de dilatação linear do aço igual a 11.10^-6ºC^-1.

Ver Resposta

Para encontrar o comprimento final do fio, primeiro vamos calcular a sua variação para essa variação de temperatura. Para isso, basta substituir na fórmula:

ΔL = L₀.α.Δθ
ΔL = 20.11.10^-6.(100-40)
ΔL = 20.11.10^-6.(60)
ΔL = 20.11.60.10^-6
ΔL = 13200.10^-6
ΔL = 0,0132

Para sabermos o tamanho final do fio de aço, temos de somar o comprimento inicial com a variação encontrada:

L = L0+ΔL
L = 20+0,0132
L = 20,0132 m

Exercício 2

Uma chapa quadrada de alumínio, possui lados iguais a 3 m quando sua temperatura é igual a 80 ºC. Qual será a variação da sua área, se a chapa for submetida a uma temperatura de 100 ºC? Considere o coeficiente de dilatação linear do alumínio 22.10^-6 ºC^-1.

Ver Resposta

Como a chapa é quadrada, para encontrar a medida da área inicial devemos fazer:

A₀ = 3.3 = 9 m²

Foi informado o valor do coeficiente de dilatação linear do alumínio, entretanto, para calcular a variação superficial necessitamos do valor do β. Desta forma, primeiro vamos calcular esse valor:

β = 2. 22.10^-6 ºC^-1 = 44.10^-6 ºC

Podemos agora calcular a variação da área da chapa, substituindo os valores na fórmula:

ΔA = A₀.β.Δθ
ΔA = 9.44.10^-6.(100-80)
ΔA = 9.44.10^-6.(20)
ΔA = 7920.10^-6
ΔA = 0,00792 m²

A Variação da área é de 0,00792 m².

Exercício 3

Um frasco de vidro de 250 ml contém 240 ml de álcool a uma temperatura de 40 ºC. A que temperatura o álcool começará a transbordar do frasco? Considere o coeficiente de dilatação linear do vidro igual a 8.10^-6 ºC^-1 e o coeficiente volumétrico do álcool 11,2.10^-4 ºC^-1.

Ver Resposta

Primeiro precisamos calcular o coeficiente volumétrico do vidro, pois foi informado apenas o seu coeficiente linear. Assim, temos:

γ_Vidro = 3 . 8 . 10^-6 = 24 . 10^-6 ºC ^-1

Tanto o frasco quanto o álcool sofrem dilatação e o álcool começará a trasbordar quando seu volume for maior que o volume do frasco.

Quando os dois volumes forem iguais, o álcool ficará na iminência de transbordar do frasco. Nesta situação, temos que o volume do álcool é igual ao volume do frasco de vidro, ou seja, V_vidro = V_álcool.

O volume final é encontrado fazendo-se V = V₀ + ΔV. Substituindo na expressão acima, temos:

V_{0 vidro}+ ΔV_vidro = V₀_álcool+ ΔV_álcool

Substituindo os valores do problema:

250 + (250 . 24 . 10^-6. Δθ) = 240 + (240 . 11,2 . 10^-4. Δθ)
250 + (0,006 . Δθ) = 240 + (0,2688 . Δθ)
0,2688 . Δθ - 0,006 . Δθ = 250 - 240
0,2628. Δθ = 10
Δθ = 38 ºC

Para sabermos a temperatura final, temos de somar a temperatura inicial com a sua variação:

T=T₀+ΔT
T=40+38
T=78 ºC

Estude com mais

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações