Equação do Segundo Grau

Rafael C. Asth

Professor de Matemática e Física

A equação do segundo grau recebe esse nome porque é uma equação polinomial cujo termo de maior grau está elevado ao quadrado. Também chamada de equação quadrática, é representada por:

Numa equação do 2º grau, o x é a incógnita e representa um valor desconhecido. Já as letras a, b e c são chamadas coeficientes da equação.

Os coeficientes são números reais e o coeficiente a tem que ser diferente de zero, pois do contrário passa a ser uma equação do 1º grau.

Resolver uma equação de segundo grau, significa determinar os valores reais de x, que tornam a equação verdadeira. Esses valores são denominados raízes da equação.

Uma equação do segundo grau possui no máximo duas raízes reais.

Equações do 2º Grau Completas e Incompletas

As equações do 2º grau completas são aquelas que apresentam todos os coeficientes, ou seja a, b e c são diferentes de zero (a, b, c ≠ 0).

Por exemplo, a equação 5x² + 2x + 2 = 0 é completa, pois todos os coeficientes são diferentes de zero (a = 5, b = 2 e c = 2).

Uma equação do segundo grau é incompleta quando b = 0 ou c = 0 ou b = c = 0.

Exemplo 1 — equações do 2° grau incompletas

Exemplo 2
Determine os valores de x que tornam a equação 4x² - 16 = 0 verdadeira.

Solução:

A equação dada é uma equação incompleta do 2º grau, com b = 0. Para equações deste tipo, podemos resolver, isolando o x. Assim:

Note que a raiz quadrada de 4 pode ser 2 e - 2, pois esses dois números elevados ao quadrado resultam em 4.

Assim, as raízes da equação 4x² - 16 = 0 são x = - 2 e x = 2

Exemplo 3
Encontre o valor do x para que a área do retângulo abaixo seja igual a 2.

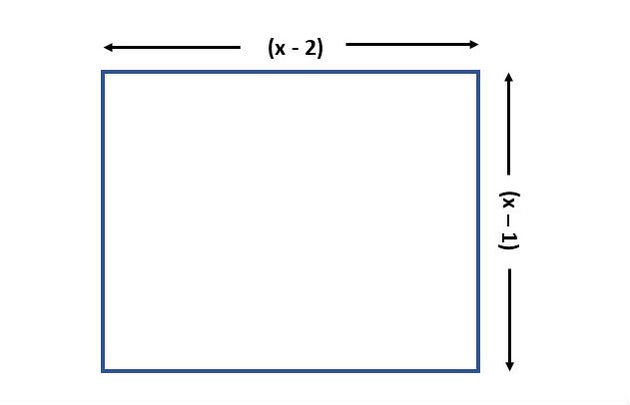
Solução:

A área do retângulo é encontrada multiplicando-se a base pela altura. Assim, devemos multiplicar os valores dados e igualar a 2.

(x - 2) . (x - 1) = 2

Agora vamos multiplicar todos os termos:

x . x - 1 . x - 2 . x - 2 . (- 1) = 2
x² - 1x - 2x + 2 = 2
x² - 3x + 2 - 2 = 0
x² - 3x = 0

Após resolver as multiplicações e simplificações, encontramos uma equação incompleta do segundo grau, com c = 0.

Esse tipo de equação pode ser resolvida através da fatoração, pois o x se repete em ambos os termos. Assim, iremos colocá-lo em evidência.

x . (x - 3) = 0

Para o produto ser igual a zero, ou x = 0 ou (x - 3) = 0. Contudo, substituindo x por zero, as medidas dos lados ficam negativas, portanto, esse valor não será resposta da questão.

Então, temos que o único resultado possível é (x - 3) = 0. Resolvendo essa equação:

x - 3 = 0
x = 3

Desta forma, o valor do x para que a área do retângulo seja igual a 2 é x = 3.

Fórmula de Bhaskara

Quando uma equação do segundo grau é completa, usamos a Fórmula de Bhaskara para encontrar as raízes da equação.

A fórmula é apresentada abaixo:

Fórmula do Delta

Na fórmula de Bhaskara, aparece a letra grega Δ (delta), chamada discriminante da equação, pois conforme o seu valor é possível saber qual o número de raízes (soluções) que a equação terá.

Para determinar o delta usamos a seguinte fórmula:

Passo a Passo

Para resolver uma equação do 2º grau, usando a fórmula de Bhaskara, devemos seguir os seguintes passos:

1º Passo: Identificar os coeficientes a, b e c.

Nem sempre os termos da equação aparecem na mesma ordem, portanto, é importante saber identificar os coeficientes, independente da sequência em que estão.

O coeficiente a é o número que está junto ao x², o b é o número que acompanha o x e o c é o termo independente, ou seja, o número que aparece sem o x.

2º Passo: Calcular o delta.

Para calcular as raízes é necessário conhecer o valor do delta. Para isso, substituímos as letras na fórmula pelos valores dos coeficientes.

Podemos, a partir do valor do delta, saber previamente o número de raízes que terá a equação do 2º grau. Ou seja, se o valor de Δ for maior que zero (Δ > 0), a equação terá duas raízes reais e distintas.

Se ao contrário, delta for menor que zero (Δ < 0), a equação não apresentará raízes reais e se for igual a zero (Δ = 0), a equação apresentará somente uma raiz.

3º Passo: Calcular as raízes.

Se o valor encontrado para delta for negativo, não precisa fazer mais nenhum cálculo e a resposta será que a equação não possui raízes reais.

Caso o valor do delta seja igual ou maior que zero, devemos substituir todas as letras pelos seus valores na fórmula de Bhaskara e calcular as raízes.

Exemplo 4
Determine as raízes da equação 2x² - 3x - 5 = 0

Solução:

Para resolver, primeiro devemos identificar os coeficientes, assim temos:

a = 2
b = - 3
c = - 5

Agora, podemos encontrar o valor do delta. Devemos tomar cuidado com as regras de sinais e lembrar que primeiro devemos resolver a potenciação e a multiplicação e depois a soma e a subtração.

Δ = (- 3)² - 4 . (- 5) . 2 = 9 +40 = 49

Como o valor encontrado é positivo, encontraremos dois valores distintos para as raízes. Assim, devemos resolver a fórmula de Bhaskara duas vezes. Temos então:

Assim, as raízes da equação 2x² - 3x - 5 = 0 são x = 5/2 e x = - 1.

Sistema de Equações do 2º Grau

Quando queremos encontrar valores de duas incógnitas diferentes que satisfaçam simultaneamente duas equações, temos um sistema de equações.

As equações que formam o sistema podem ser do 1º grau e do 2º grau. Para resolver esse tipo de sistema podemos usar o método da substituição e o método da adição.

Exemplo 5
Resolva o sistema abaixo:

Solução:

Para resolver o sistema, podemos utilizar o método da adição. Neste método, somamos os termos semelhantes da 1ª equação com os da 2ª equação. Assim, reduzimos o sistema para uma só equação.

Podemos ainda simplificar todos os termos da equação por 3 e o resultado será a equação x² - 2x - 3 = 0. Resolvendo a equação, temos:

Δ = 4 - 4 . 1 . (- 3) = 4 + 12 = 16

Depois de encontrar os valores do x, não podemos esquecer que temos ainda de encontrar os valores de y que tornam o sistema verdadeiro.

Para isso, basta substituir os valores encontrados para o x, em uma das equações.

y₁ - 6. 3 = 4
y₁ = 4 + 18
y₁ = 22

y₂ - 6 . (-1) = 4
y₂ + 6 = 4
y₂ = - 2

Portanto, os valores que satisfazem ao sistema proposto são (3, 22) e (- 1, - 2)

Você também pode se interessar por Equação do Primeiro Grau.

Exercícios de equação do segundo grau

Questão 1

Resolva a equação de segundo grau completa, utilizando a Fórmula de Bhaskara:

2x² + 7x + 5 = 0

Confira mais questões em Equação do 2º Grau - Exercícios

Questão 2

Resolva as equações incompletas do segundo grau:

a) 5x² – x = 0

b) 2x² – 2 = 0

c) 5x² = 0

Para saber mais, leia também:

• Função Quadrática
• Soma e Produto
• Inequação
• Equações Irracionais
• Vértice da Parábola
• Exercícios de equação biquadrada

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.