🚀 60% OFF para turbinar seus estudos! Assine agora
Acelere seu aprendizado
ASSINAR TM +

Exercícios de dilatação térmica

Rafael C. Asth
Rafael C. Asth
Professor de Matemática e Física
Remover anúncios

A dilatação térmica é um fenômeno fundamental na física que descreve a variação das dimensões de um material em resposta às mudanças de temperatura. Para aprender mais sobre dilatação térmica: linear, superficial e volumétrica, pratique com nossos exercícios e tire suas dúvidas com as respostas explicadas.

Questão 1 (dilatação linear)

Um trilho de trem de 10 metros de comprimento está inicialmente a 20 °C. Se ele for aquecido até 60 °C, seu novo comprimento aumentará

Considere o coeficiente de dilatação linear para o aço do trilho igual a 12 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço sinal de grau C à potência de menos 1 fim do exponencial.

a) menos de 0,1% do comprimento inicial.

b) entre 0,1% e 1% do comprimento inicial.

c) mais de 1% e menos que 2% do comprimento inicial.

d) mais de 2% e menos que 3% do comprimento inicial.

e) mais de 3% e menos que 4% do comprimento inicial.

Gabarito explicado

Resposta: a) menos de 0,1% do comprimento inicial.

Explicação:

Podemos usar a equação de dilatação linear:

ΔL = L . α . ΔT

Onde:

ΔL = aumento no comprimento;

α = coeficiente de dilatação linear do material;

L = comprimento inicial;

ΔT = variação de temperatura.

Aplicando os valores:

reto delta maiúsculo reto L igual a espaço reto L com 0 subscrito espaço. espaço reto alfa espaço. espaço espaço reto delta maiúsculo reto Treto delta maiúsculo reto L igual a espaço 10 espaço. espaço 12 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço. espaço espaço parêntese esquerdo 60 espaço menos espaço 20 parêntese direitoreto delta maiúsculo reto L igual a espaço 10 espaço. espaço 12 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço. espaço espaço 40reto delta maiúsculo reto L igual a espaço 4 espaço 800 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço reto mreto delta maiúsculo reto L igual a espaço 0 vírgula 0048 espaço espaço reto m

Portanto, o aumento no comprimento é de 0,0048 metros, sendo menos de 0,1%, pois:

0 vírgula 1 sinal de percentagem espaço de espaço 10 espaço reto m espaço igual a espaço numerador 0 vírgula 1 sobre denominador 100 fim da fração espaço. espaço 10 espaço igual a 0 vírgula 01

Sendo 0,0048 ＜ 0,01.

Questão 2 (dilatação linear)

Considere uma barra de alumínio de 2 metros de comprimento a 25 °C. Se a barra for aquecida para 75 °C, qual será a variação do comprimento?

Considere o coeficiente de dilatação linear do alumínio 22 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço sinal de grau C à potência de menos 1 fim do exponencial.

a) 0,0005 metros

b) 0,0010 metros

c) 0,0015 metros

d) 0,0022 metros

e) 0,0025 metros

Gabarito explicado

Resposta: a resposta correta é a alternativa (d) 0,0022 metros.

Explicação:

Usando a equação de dilatação linear:

ΔL = Li . α . ΔT

Onde:

ΔL = aumento no comprimento

α = coeficiente de dilatação linear do alumínio

Li = comprimento inicial

ΔT = variação de temperatura

Substituindo os valores na fórmula:

reto delta maiúsculo reto L igual a espaço Li espaço. espaço reto alfa espaço. espaço reto delta maiúsculo reto T espaço espaçoreto delta maiúsculo reto L igual a espaço 2 espaço. espaço 22 espaço. espaço 10 à potência de menos 6 fim do exponencial. espaço parêntese esquerdo 75 sinal de grau reto C espaço menos espaço 25 sinal de grau reto C parêntese direito espaço espaçoreto delta maiúsculo reto L igual a espaço 2 espaço. espaço 22 espaço. espaço 10 à potência de menos 6 fim do exponencial. espaço espaço 50reto delta maiúsculo reto L igual a 2 espaço 200 espaço espaço. espaço 10 à potência de menos 6 fim do exponencialreto delta maiúsculo reto L igual a espaço 0 vírgula 0022 espaço reto m

Portanto, a variação do comprimento é de 0,0022 metros.

Questão 3 (dilatação linear)

Uma barra metálica é utilizada em uma ponte suspensa. O comprimento inicial da barra é 15,0 m. Durante um inverno rigoroso, a temperatura diminui, causando a contração térmica da barra. Considerando que o coeficiente de dilatação linear do metal da barra (reto alfa) é 8 sinal de multiplicação 10 à potência de menos 6 fim do exponencial espaço sinal de grau C à potência de menos 1 fim do exponencial, qual será o novo comprimento da barra se a temperatura diminuir 20 ∘C?

a) 15,30001 m

b) 14,9976 m

c) 14,7887 m

d) 14,4241 m

e) 13,6201 m

Gabarito explicado

Resposta Correta:

B) 14,9976 m

Explicação Passo a Passo:

A contração térmica de um material é dada pela fórmula:

ΔL = Li . α . ΔT

onde:

ΔL é a variação no comprimento;

Li é o comprimento inicial;

α é o coeficiente de dilatação linear;

ΔT é a variação de temperatura.

Os dados fornecidos pelo enunciado são:

Li = 15,0 m

α = 8 sinal de multiplicação 10 à potência de menos 6 fim do exponencial espaço sinal de grau reto C à potência de menos 1 fim do exponencial

ΔT = −20 °C

Substituindo os valores na fórmula:

reto delta maiúsculo reto L espaço igual a espaço Li espaço. espaço reto alfa espaço. espaço reto delta maiúsculo reto T espaço espaçoreto delta maiúsculo reto L igual a espaço parêntese esquerdo 15 vírgula 0 espaço reto m parêntese direito espaço. espaço parêntese esquerdo 8.10 à potência de menos 6 fim do exponencial espaço sinal de grau reto C à potência de menos 1 fim do exponencial parêntese direito espaço. espaço parêntese esquerdo menos 20 espaço operador anelar reto C parêntese direitoreto delta maiúsculo reto L igual a espaço menos 2400 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço reto m

Calculando o novo comprimento:

L espaço igual a espaço L com i subscrito espaço mais espaço L com i subscrito espaço. espaço alfa espaço. espaço incremento TL espaço igual a espaço 15 espaço menos espaço 2400 espaço. espaço 10 à potência de menos 6 fim do exponencialL espaço igual a espaço 15 espaço menos espaço 0 vírgula 0024L espaço igual a espaço 14 vírgula 9976 espaço m

Portanto, a resposta correta é a alternativa (B), e o novo comprimento da barra após a contração térmica é de 14,9976 m.

Remover anúncios

Questão 4 (dilatação linear)

(Enem 2012)

O quadro oferece os coeficientes de dilatação linear de alguns metais e ligas metálicas:

Para permitir a ocorrência do fato observado na tirinha, a partir do menor aquecimento do conjunto, o parafuso e a porca devem ser feitos, respectivamente, de

a) aço e níquel.

b) alumínio e chumbo.

c) platina e chumbo.

d) ouro e latão.

e) cobre e bronze.

Gabarito explicado

Resposta correta: c) platina e chumbo.

É necessário que a porca sofra a maior dilatação térmica possível, enquanto o parafuso, a menor possível.

Assim, para a porca, o maior coeficiente de dilatação linear é a platina. Para o parafuso, o menor coeficiente de dilatação linear é o do chumbo.

Questão 5 (dilatação superficial)

Uma placa de vidro tem uma área de 1 m² a 25 °C. Quando a temperatura aumenta para 75 °C, qual é a nova área da placa?

Considere o coeficiente de dilatação linear do vidro como 9 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço sinal de grau C à potência de menos 1 fim do exponencial.

a) 1,0004 m²

b) 1,0002 m ²

c) 1,0006 m²

d) 1,0008 m²

e) 1,0009 m²

Gabarito explicado

Resposta correta: alternativa e) 1,0009 m².

Explicação:

O enunciado informa o coeficiente de dilatação linear, mas precisamos do superficial, sendo este o dobro do linear.

reto beta igual a 2 reto alfareto beta igual a 2 espaço. espaço 9 espaço. espaço 10 à potência de menos 6 fim do exponencialreto beta igual a 18 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço sinal de grau reto C à potência de menos 1 fim do exponencial

Utilizamos a fórmula da dilatação superficial:

incremento reto A igual a reto A com reto i subscrito espaço. espaço reto beta espaço. espaço incremento reto T

Onde,

  • incremento reto A é a variação da área;
  • reto A com reto i subscrito espaçoé a área inicial;
  • beta o coeficiente de dilatação superficial;
  • incremento reto T variação da temperatura.

Substituindo os valores na fórmula:

incremento reto A igual a reto A com reto i subscrito espaço. espaço reto beta espaço. espaço incremento reto Tincremento reto A igual a 1 espaço. espaço 18 espaço. espaço 10 à potência de menos 6 fim do exponencial. espaço parêntese esquerdo 75 menos 25 parêntese direitoincremento reto A igual a 1 espaço. espaço 18 espaço. espaço 10 à potência de menos 6 fim do exponencial. espaço 50incremento reto A igual a 900 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço reto m ao quadradoincremento reto A igual a 0 vírgula 0009 espaço reto m ao quadrado

Somando ao valor inicial:

0 vírgula 0009 espaço mais espaço 1 espaço igual a espaço 1 vírgula 0009 espaço reto m ao quadrado

Questão 6 (dilatação superficial)

Em uma missão espacial, uma antena parabólica composta por uma malha metálica é enviada para um planeta distante. O coeficiente de dilatação superficial da malha metálica é reto beta igual a 2 sinal de multiplicação 10 à potência de menos 5 fim do exponencial espaço sinal de grau reto C à potência de menos 1 fim do exponencial. A antena tem uma área inicial de 20 m² a uma temperatura inicial de 30 °C. Quando a antena chega ao planeta, a temperatura diminui para -50 °C. Qual é a nova área da antena parabólica?

a) 17,531 m²

b) 19,501 m²

c) 18,223 m²

d) 19,968 m²

e) 20,8 m²

Gabarito explicado

Resposta correta: d) 19,968 m²

A variação na área de uma superfície devido à dilatação/contração térmica superficial é dada por:

ΔA=β⋅Ai⋅ΔT

onde:

  • ΔA é a variação na área;
  • β é o coeficiente de dilatação superficial;
  • Ai é a área inicial;
  • ΔT é a variação de temperatura.

Dados informados no enunciado:

  • Ai = 20 m²;
  • reto beta igual a 2 sinal de multiplicação 10 à potência de menos 5 fim do exponencial espaço sinal de grau reto C à potência de menos 1 fim do exponencial;
  • ΔT (variação de temperatura) = − 50 °C − 30 °C = − 80 °C.

Substituir os valores na fórmula:

reto delta maiúsculo reto A igual a reto beta vezes Ai vezes reto delta maiúsculo reto Treto delta maiúsculo reto A igual a 2 espaço. espaço 10 à potência de menos 5 fim do exponencial vezes 20 vezes parêntese esquerdo menos 80 parêntese direitoreto delta maiúsculo reto A igual a menos 3200 espaço. espaço 10 à potência de menos 5 fim do exponencial espaço reto m ao quadrado

Calculo da nova área

A nova área é a área inicial mais a variação.

A espaço igual a espaço A i espaço menos 3200 espaço. espaço 10 à potência de menos 5 fim do exponencialA espaço igual a 20 espaço menos espaço 0 vírgula 032A espaço igual a espaço 19 vírgula 968 espaço m ao quadrado

Portanto, a resposta correta é a alternativa (d), e a nova área da antena parabólica após a contração térmica superficial é de 19,968 m².

Remover anúncios

Questão 7 (dilatação superficial)

Um pesquisador deseja descobrir o coeficiente de dilatação superficial de um dado material. Para isso, aquece uma barra de 0 °C a 50 °C e anota seus comprimentos inicial e final. Utilizando um programa gráfico de computador, ele desenha o seguinte gráfico:

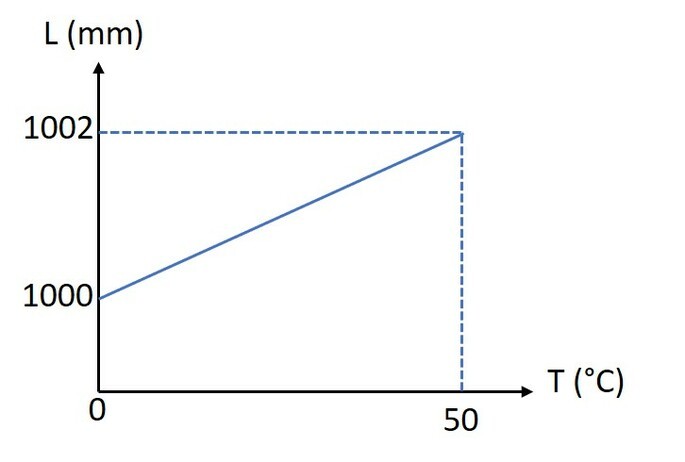
Gráfico de dilatação térmica.

Com base no gráfico, o coeficiente de dilatação superficial é

a) reto beta igual a 2. espaço 10 à potência de menos 5 fim do exponencial espaço sinal de grau reto C à potência de menos 1 fim do exponencial

b) reto beta igual a 4. espaço 10 à potência de menos 5 fim do exponencial espaço sinal de grau reto C à potência de menos 1 fim do exponencial

c) reto beta igual a 8. espaço 10 à potência de menos 5 fim do exponencial espaço sinal de grau reto C à potência de menos 1 fim do exponencial

d) reto beta igual a 12 espaço. espaço 10 à potência de menos 5 fim do exponencial espaço sinal de grau reto C à potência de menos 1 fim do exponencial

e) reto beta igual a 16. espaço 10 à potência de menos 5 fim do exponencial espaço sinal de grau reto C à potência de menos 1 fim do exponencial

Gabarito explicado

Resposta correta: c) reto beta igual a 8. espaço 10 à potência de menos 5 fim do exponencial espaço sinal de grau reto C à potência de menos 1 fim do exponencial.

O gráfico exibe as variações lineares da barra em função da temperatura. Podemos determinar o coeficiente de dilatação linear e, após, multiplicar por dois, para obter o superficial.

incremento reto L igual a Li espaço. espaço reto alfa espaço. espaço incremento reto T1002 espaço menos espaço 1000 espaço igual a espaço 1000 espaço. espaço reto alfa espaço. espaço 502 espaço igual a 50 espaço 000 reto alfareto alfa igual a numerador 2 sobre denominador 50 espaço 000 fim da fraçãoreto alfa igual a 4 espaço. espaço 10 à potência de menos 5 fim do exponencial espaço sinal de grau reto C à potência de menos 1 fim do exponencial

Para obter o superficial:

reto beta igual a 2 reto alfareto beta igual a 2 espaço. espaço 4 espaço. espaço 10 à potência de menos 5 fim do exponencial espaço sinal de grau reto C à potência de menos 1 fim do exponencialreto beta igual a 8. espaço 10 à potência de menos 5 fim do exponencial espaço sinal de grau reto C à potência de menos 1 fim do exponencial

Questão 8 (dilatação volumétrica)

(Enem 2009) Durante uma ação de fiscalização em postos de combustíveis, foi encontrado um mecanismo inusitado para enganar o consumidor. Durante o inverno, o responsável por um posto de combustível compra álcool por R$ 0,50/litro, a uma temperatura de 5 °C. Para revender o líquido aos motoristas, instalou um mecanismo na bomba de combustível para aquecê-lo, para que atinja a temperatura de 35 °C, sendo o litro de álcool revendido a R$ 1,60. Diariamente o posto compra 20 mil litros de álcool a 5 °C e os revende.

Com relação à situação hipotética descrita no texto e dado que o coeficiente de dilatação volumétrica do álcool é de 1 sinal de multiplicação 10 à potência de menos 3 fim do exponencial espaço º reto C à potência de menos 1 fim do exponencial, desprezando-se o custo da energia gasta no aquecimento do combustível, o ganho financeiro que o dono do posto teria obtido devido ao aquecimento do álcool após uma semana de vendas estaria entre

a) R$ 500,00 e R$ 1.000,00.

b) R$ 1.050,00 e R$ 1.250,00.

c) R$ 4.000,00 e R$ 5.000,00.

d) R$ 6.000,00 e R$ 6.900,00.

e) R$ 7.000,00 e R$ 7.950,00.

Gabarito explicado

Resposta correta: d) R$ 6.000,00 e R$ 6.900,00.

Sendo 20 000 L por dia, em uma semana:

20 000 x 7 = 140 000 L

A dilatação volumétrica será:

incremento reto V igual a Vi espaço. espaço reto lambda espaço. espaço incremento reto T

Substituindo os valores fornecidos:

incremento reto V igual a Vi espaço. espaço reto lambda espaço. espaço incremento reto Tincremento reto V igual a 140 espaço 000 espaço. espaço 1 espaço. espaço 10 à potência de menos 3 fim do exponencial espaço. espaço parêntese esquerdo 35 espaço menos espaço 5 parêntese direitoincremento reto V igual a 140 espaço 000 espaço. espaço 1 espaço. espaço 10 à potência de menos 3 fim do exponencial espaço. espaço 30incremento reto V igual a 4 espaço 200 espaço 000 espaço. espaço 10 à potência de menos 3 fim do exponencial espaçoincremento reto V igual a 4 espaço 200 espaço reto L espaço

Considerando o preço de revendo R$1,60.

4 200 x 1,60 = 6 720

Questão 9 (dilatação volumétrica)

Em um laboratório de pesquisa, um engenheiro está trabalhando com um material cujo coeficiente de dilatação linear (α) é 1 vírgula 5 sinal de multiplicação 10 à potência de menos 5 fim do exponencial espaço sinal de grau C à potência de menos 1 fim do exponencial. Ele precisa calcular a variação volumétrica de uma amostra desse material quando aquecida de 20 °C para 120 °C. A variação volumétrica deste material em relação ao volume inicial será de

a) 0,0036Vi m³

b) 0,0038 Vi m³

c) 0,0042Vi m³

d) 0,0045Vi m³

e) 0,0048Vi m³

Gabarito explicado

Resposta Correta: d) 0,0045 Vi m³

Identificação dos Dados:

Coeficiente de dilatação linear (α) = 1 vírgula 5 sinal de multiplicação 10 à potência de menos 5 fim do exponencial espaço sinal de grau reto C à potência de menos 1 fim do exponencial.

Temperatura inicial (T1) = 20 °C

Temperatura final (T2) = 120 °C

Cálculo da Variação Volumétrica:

Como o coeficiente informado é o linear, devemos multiplicar por três para obter o volumétrico.

reto delta maiúsculo reto V espaço igual a espaço Vi espaço vezes espaço 3 reto alfa espaço vezes espaço parêntese esquerdo reto T 2 menos reto T 1 parêntese direitoreto delta maiúsculo reto V espaço igual a espaço Vi espaço vezes espaço 3 espaço. espaço 1 vírgula 5 espaço. espaço 10 à potência de menos 5 fim do exponencial espaço vezes espaço parêntese esquerdo 120 menos 20 parêntese direitoreto delta maiúsculo reto V espaço igual a espaço Vi espaço vezes espaço 3 espaço. espaço 1 vírgula 5 espaço. espaço 10 à potência de menos 5 fim do exponencial espaço vezes espaço 100reto delta maiúsculo reto V espaço igual a espaço 450 espaço. espaço 10 à potência de menos 5 fim do exponencial espaço Vireto delta maiúsculo reto V espaço igual a espaço 0 vírgula 0045 espaço Vi

Portanto, a resposta correta é a alternativa d. 0,0045.Vi é a variação volumétrica do material ao ser aquecido de 20 °C para 120 °C.

Remover anúncios

Questão 10 (dilatação volumétrica)

Um grupo de engenheiros está trabalhando em uma máquina térmica. Esta máquina produz energia térmica por meio de reações químicas. Ao aquecer, os materiais sofrem dilatação térmica, onde um componente pode se dilatar no máximo 0,001% do seu volume.

O volume inicial do componente, feito de um material com coeficiente de dilatação volumétrica de 1 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço sinal de grau C à potência de menos 1 fim do exponencial, é de 100 cm³.

A máxima variação de temperatura que este componente poderá sofrer é de

a) 10 °C

b) 50 °C

c) 100° C

d) 150 °C

e) 200 °C

Gabarito explicado

Resposta correta: a) 10° C

Para calcular a máxima variação em graus Celsius, primeiro, devemos calcular a máxima variação de volume, sendo 0,001% do volume inicial.

0 vírgula 001 sinal de percentagem espaço igual a espaço numerador 0 vírgula 001 sobre denominador 100 fim da fração igual a 0 vírgula 00001

Volume máximo = Volume inicial . 1,00001

100 cm³ . 1,00001 = 100,001 cm³

Substituindo os valores na fórmula da dilatação volumétrica:

V com f subscrito igual a V com i subscrito espaço mais espaço V com i subscrito. gama. incremento T100 vírgula 001 espaço igual a espaço 100 espaço mais espaço 100 espaço. espaço 1 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço. espaço incremento T100 vírgula 001 espaço igual a espaço 100 espaço mais espaço 100 espaço. espaço 10 à potência de menos 6 fim do exponencial espaço. espaço incremento T100 vírgula 001 espaço menos espaço 100 espaço igual a espaço 10 à potência de menos 4 fim do exponencial espaço. espaço incremento Tnumerador 0 vírgula 001 sobre denominador 10 à potência de menos 4 fim do exponencial fim da fração igual a incremento T10 à potência de menos 3 fim do exponencial sobre 10 à potência de menos 4 fim do exponencial igual a incremento T10 à potência de menos 3 menos parêntese esquerdo menos 4 parêntese direito fim do exponencial igual a incremento T10 à potência de menos 3 mais 4 fim do exponencial igual a incremento T10 espaço igual a incremento Tespaço

Questão 11 (dilatação volumétrica)

Utilizando uma peça metálica com coeficiente de dilatação volumétrica reto lambda igual a 6 sinal de multiplicação 10 à potência de menos 5 espaço fim do exponencial sinal de grau reto C à potência de menos 1 fim do exponencial, os cientistas realizaram experimentos medindo o volume em diferentes temperaturas. Os dados coletados são:

Temperatura (°C) Volume (m³)
20 2
40 2,01
60 2,02
80 2,03
100 2,04

Com base nesses dados, desenhe um gráfico que represente a variação do volume em função da temperatura. Considere uma escala adequada para ambos os eixos. Este gráfico de ser

a) uma linha reta inclinada positivamente.

b) uma linha reta inclinada negativamente.

c) uma curva ascendente.

d)uma curva descendente.

e) uma linha horizontal.

Gabarito explicado

Resposta correta: a) O gráfico deve ser uma linha reta inclinada positivamente.

A função que modela a variação do volume pelo tempo é:

reto V parêntese esquerdo reto t parêntese direito igual a Vi espaço mais espaço Vi. reto gama. incremento reto T espaço

O volume inicial Vi e o coeficiente de dilatação volumétrica são constantes, logo, a volume depende apenas da variação da temperatura.

É essa é uma função polinomial do 1º grau, seu gráfico é uma reta.

O coeficiente que multiplica incremento T é o coeficiente angular, fornecendo a inclinação da reta. Sendo o coeficiente de inclinação positivo, a reta é crescente.

Questão 12 (dilatação volumétrica)

(VUNESP 2010) Nos últimos anos temos sido alertados sobre o aquecimento global. Estima-se que, mantendo-se as atuais taxas de aquecimento do planeta, haverá uma elevação do nível do mar causada, inclusive, pela expansão térmica, causando inundação em algumas regiões costeiras. Supondo, hipoteticamente, os oceanos como sistemas fechados e considerando que o coeficiente de dilatação volumétrica da água é aproximadamente 2 espaço sinal de multiplicação espaço 10 à potência de – 4 fim do exponencial espaço º C à potência de – 1 fim do exponencial e que a profundidade média dos oceanos é de 4 km, um aquecimento global de 1 ºC elevaria o nível do mar, devido à expansão térmica, em, aproximadamente,

a) 0,3 m.

b) 0,5 m.

c) 0,8 m.

d) 1,1 m.

e) 1,7 m.

Gabarito explicado

Resposta correta: c) 0,8 m.

Considerando uma coluna de 4 km de água e aplicando a fórmula da dilatação volumétrica:

incremento reto V igual a Vi espaço. espaço reto lambda espaço. espaço incremento reto Tincremento reto V igual a 4000 espaço. espaço 2 espaço. espaço 10 à potência de menos 4 fim do exponencial espaço. espaço 1incremento reto V igual a 8000 espaço. espaço 10 à potência de menos 4 fim do exponencial espaçoincremento reto V igual a 0 vírgula 8 espaço reto m

Questão 13

Conteúdo exclusivo para assinantes Toda Matéria+
Além de mais exercícios, tenha acesso a mais recursos para dar um up nos seus estudos.
Corretor de Redação para o Enem
Exercícios exclusivos
Estude sem publicidade
Assinar Toda Matéria+

Para mais exercícios de Física:

Aprenda mais sobre:

Rafael C. Asth
Rafael C. Asth
Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.
Veja também
Leitura Recomendada
Tópicos Relacionados
Exercícios Exercícios de Física Física Termologia 2º ano (Ensino Médio) Exercícios 2º ano (Ensino Médio)
Que tal um up?
Toda Matéria+
Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo
Exercícios exclusivos Acesso a centenas de questões com gabaritos
Estude sem publicidade Navegação limpa e focada para evitar distrações
Assinar Toda Matéria+
Toda Matéria no YouTube
Thumbnail Toda Matéria no Youtube
Toda Matéria Inscreva-se
Remover anúncios
Remover anúncios