Exercícios sobre PA e PG

Rafael C. Asth

Professor de Matemática e Física

Estude progressão aritmética e geométrica com exercícios resolvidos e comentados passo a passo.

Exercício 1

Em uma PA, a2 = 5 e a7 = 15. Determine a4 e some os cinco primeiros termos desta PA.

Ver Resposta

Resposta correta: a4 = 9 e S = 35.

Resolução

1º passo: determinar a razão e a4.
Para sair de a2 e chegar em a7, somamos 5r, pois é a "distância" entre 7 e 2.

$a com 7 subscrito igual a a com 2 subscrito mais 5 r 15 espaço igual a espaço 5 espaço mais espaço 5 r 15 espaço menos espaço 5 espaço igual a 5 r 10 espaço igual a espaço 5 r 10 sobre 5 igual a r 2 igual a r$

O termo a4 é o termo a2 mais 2r, pois, para sair de a2 e chegar em a4, "avançamos" 2r. Logo,

$a com 4 subscrito igual a a com 2 subscrito mais 2 r a com 4 subscrito igual a 5 espaço mais espaço 2.2 a com 4 subscrito igual a 5 espaço mais espaço 4 espaço igual a espaço 9$

Portanto, o quarto termo da PA é 9.

2º passo: determinar a soma dos cinco primeiros termos desta PA.

A soma dos termos de uma PA é dada por:

$S igual a numerador parêntese esquerdo a com 1 subscrito mais a com n subscrito parêntese direito. n sobre denominador 2 fim da fração$

a1 = a2 - r (pois retrocedemos uma posição na PA, a partir do a2)
a1 = 5 - 2 = 3

a5 = a7 - 2r (pois retrocedemos duas posições na PA, a partir do a7).
a5 = 15 - 2.2 = 15 - 4 = 11

$S igual a numerador parêntese esquerdo 3 espaço mais espaço 11 parêntese direito.5 sobre denominador 2 fim da fração igual a numerador 14 espaço. espaço 5 sobre denominador 2 fim da fração igual a 70 sobre 2 igual a 35$

Exercício 2

(Aeronáutica 2021) Um professor escreveu uma progressão aritmética crescente de 8 termos começando pelo número 3 e composta apenas de números naturais. Ele notou, então, que o segundo, o quarto e o oitavo termos dessa progressão aritmética formavam, nessa ordem, uma progressão geométrica. O professor observou também que a soma dos termos dessa progressão geométrica era igual a

a) 42
b) 36
c) 18
d) 9

Ver Resposta

Resposta: a) 42

Pela PA, os termos que formam uma PG são a2, a4 e a8:

$a com 2 subscrito igual a a com 1 subscrito mais parêntese esquerdo n menos 1 parêntese direito r a com 2 subscrito igual a 3 mais parêntese esquerdo 2 menos 1 parêntese direito r a com 2 subscrito igual a 3 mais espaço r$

$a com 4 subscrito igual a a com 1 subscrito mais parêntese esquerdo 4 menos 1 parêntese direito r a com 4 subscrito igual a 3 espaço mais espaço 3 r$

$a com 8 subscrito igual a 3 mais parêntese esquerdo 8 menos 1 parêntese direito r a com 8 subscrito igual a 3 mais 7 r$

A soma dos três termos é:

$S igual a a com 2 subscrito mais a com 4 subscrito mais a com 8 subscrito S igual a parêntese esquerdo 3 mais r parêntese direito espaço mais espaço parêntese esquerdo 3 mais 3 r parêntese direito espaço mais espaço parêntese esquerdo 3 mais 7 r parêntese direito S igual a 9 espaço mais espaço 11 r espaço espaço espaço parêntese esquerdo e q u a ç ã o espaço I parêntese direito$

Para determinar r, utilizamos a média geométrica:

$a com 4 subscrito igual a raiz quadrada de a com 2 subscrito. a com 8 subscrito fim da raiz 3 mais 3 r igual a raiz quadrada de parêntese esquerdo 3 mais r parêntese direito. parêntese esquerdo 3 mais 7 r parêntese direito fim da raiz$

Elevando os dois lados ao quadrado

$parêntese esquerdo 3 mais 3 r parêntese direito ao quadrado igual a parêntese esquerdo 3 mais r parêntese direito. parêntese esquerdo 3 mais 7 r parêntese direito$

Elevando o primeiro termo ao quadrado e fazendo a distributiva no segundo:

$parêntese esquerdo 3 mais 3 r parêntese direito ao quadrado igual a parêntese esquerdo 3 mais r parêntese direito. parêntese esquerdo 3 mais 7 r parêntese direito 9 espaço mais espaço 18 r espaço mais espaço 9 r ao quadrado igual a 9 espaço mais espaço 21 r espaço mais espaço 3 r espaço mais espaço 7 r ao quadrado 9 r ao quadrado menos 7 r ao quadrado igual a 24 r espaço menos espaço 18 r espaço mais espaço 9 espaço menos espaço 9 2 r ao quadrado igual a 6 r r ao quadrado igual a 3 r r. r espaço igual a espaço 3 r r espaço igual a numerador 3 r sobre denominador r fim da fração igual a 3$

Substituindo r na equação I, temos:

$S espaço igual a espaço 9 espaço mais espaço 11 r S espaço igual a espaço 9 espaço mais espaço 11.3 S espaço igual a espaço 9 espaço mais espaço 33 S espaço igual a espaço 42$

Portanto, a soma dos três primeiros termos é igual a 42.

Exercício 3

(PM-SP 2019) Em 2015, uma grande empresa petrolífera iniciou o processo de reutilização da água usada para o resfriamento das peças que produzia e fez uma projeção de aumento gradual, em progressão aritmética, até o ano de 2050, do volume de água que será reutilizada, ano a ano.

A tabela apresenta os volumes da água reutilizada, nos primeiros 3 anos:

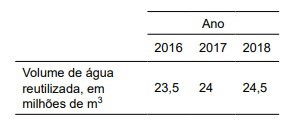
Considere que An seja o termo geral da progressão aritmética que indique o volume de água reutilizada, em milhões de m³, com n = 1, representando o volume de água reutilizada no ano de 2016, n = 2, representando o volume de água reutilizada no ano de 2017, e assim sucessivamente.

Nessas condições, tem-se que

a) An = 0,5n – 23,5.
b) An = 23,5 + 0,5n.
c) An = 0,5n + 23.
d) An = 23 – 0,5n.
e) An = 0,5n – 23.

Ver Resposta

Resposta correta: c) An = 0,5n + 23.

Objetivo
Determinar An em função de n.

Resolução
A razão da progressão aritmética é 0,5, pois 24 - 23,5 = 0,5.

a1 = 23,5

O termo geral de uma PA é dado por:

$A com n subscrito igual a espaço a com 1 subscrito espaço mais espaço parêntese esquerdo n menos 1 parêntese direito r$

Substituindo o valores:

$A com n subscrito igual a 23 vírgula 5 espaço mais espaço 0 vírgula 5 n espaço menos espaço 0 vírgula 5 A com n subscrito igual a 0 vírgula 5 n mais 23 espaço$

Exercício 4

(CEDERJ 2021) A sequência (2x+3, 3x+4, 4x+5, ...) é uma progressão aritmética de razão 6. O quarto termo dessa progressão é

a) 31.
b) 33.
c) 35.
d) 37.

Ver Resposta

Resposta correta: a) 31

Resolução
$r espaço igual a espaço a com 2 subscrito menos a com 1 subscrito 6 espaço igual a espaço 3 x mais 4 espaço menos parêntese esquerdo 2 x mais 3 parêntese direito 6 igual a 3 x mais 4 menos 2 x menos 3 6 igual a x mais 1 x igual a 6 menos 1 x igual a 5$

O quarto termo é a3 + r, desta forma:

$a com 4 subscrito igual a a com 3 subscrito mais r a com 4 subscrito igual a 4 x espaço mais espaço 5 espaço mais espaço r$

Substituindo os valores encontrados:

$a com 4 subscrito igual a 4.5 espaço mais espaço 5 espaço mais espaço 6 a com 4 subscrito igual a 20 mais espaço 5 espaço mais espaço 6 a com 4 subscrito igual a 31$

Exercício 5

(Enem 2021) No Brasil, o tempo necessário para um estudante realizar sua formação até a diplomação em um curso superior, considerando os 9 anos de ensino fundamental, os 3 anos do ensino médio e os 4 anos de graduação (tempo médio), é de 16 anos. No entanto, a realidade dos brasileiros mostra que o tempo médio de estudo de pessoas acima de 14 anos é ainda muito pequeno, conforme apresentado na tabela.

Considere que o incremento no tempo de estudo, a cada período, para essas pessoas, se mantenha constante até o ano 2050, e que se pretenda chegar ao patamar de 70% do tempo necessário à obtenção do curso superior dado anteriormente.
O ano em que o tempo médio de estudo de pessoas acima de 14 anos atingirá o percentual pretendido será

a) 2018.
b) 2023.
c) 2031.
d) 2035.
e) 2043.

Ver Resposta

Resposta correta: d) 2035.

1ª parte: determinar 70% de 16.

$70 sinal de percentagem espaço d e espaço 16 espaço igual a espaço 70 sobre 100 sinal de multiplicação 16 igual a 1120 sobre 100 igual a 11 vírgula 2$

2ª parte: determinar após quantos períodos se atingirá 11,2 anos de estudo.

A sequencia tempo de estudo é uma progressão aritmética (PA) com razão 0,6.

r = a2 - a1 = 5,8 - 5,2 = 0,6

a1 = 5,2

A quantidade 11,2 anos será atingida em:

$A com n subscrito igual a a com 1 subscrito mais espaço parêntese esquerdo n menos 1 parêntese direito r 11 vírgula 2 igual a 5 vírgula 2 mais parêntese esquerdo n menos 1 parêntese direito 0 vírgula 6 11 vírgula 2 igual a 5 vírgula 2 mais 0 vírgula 6 n menos 0 vírgula 6 11 vírgula 2 menos 5 vírgula 2 mais 0 vírgula 6 igual a 0 vírgula 6 n 6 mais 0 vírgula 6 igual a 0 vírgula 6 n 6 vírgula 6 igual a 0 vírgula 6 n numerador 6 vírgula 6 sobre denominador 0 vírgula 6 fim da fração igual a n 11 igual a n$

A quantidade de 11,2 será atingida no 11º termo da PA.

3ª parte: determinar qual é o 11º termo da PA dos anos.

A razão é a2 - a1 = 1999 - 1995 = 4 anos

$A com 11 subscrito igual a a com 1 subscrito mais parêntese esquerdo n menos 1 parêntese direito r A com 11 subscrito igual a 1995 mais parêntese esquerdo 11 menos 1 parêntese direito 4 A com 11 subscrito igual a 1995 mais 10.4 A com 11 subscrito igual a 1995 espaço mais espaço 40 A com 11 subscrito igual a 2035$

Conclusão
70% dos 16 anos requeridos para concluir um curso de graduação serão atingidos em 2035.

Exercício 6

(Corpo de Bombeiros 2021) Um avião e um caminhão de bombeiros possuem reservatórios de água com capacidades de 12 mil e 8 mil litros de água, respectivamente. O caminhão possui uma bomba de 2,5 GPM, ou seja, é capaz de bombear 2,5 galões por minuto.

A partir dessa situação hipotética, julgue o seguinte item, considerando que 1 galão seja igual a 3,8 litros de água.

Se um tanque de água possui a capacidade de X mil litros, de modo que 8, X e 12 estejam em progressão geométrica, nesta ordem, então a capacidade desse tanque é menor do que 10 mil litros.

Certo

Errado

Ver Resposta

Resposta correta: certa

Objetivo
Verificar se X < 10.

Resolução
Em uma progressão geométrica, PG, o termo do meio é a média geométrica entre os extremos.

$X menor que raiz quadrada de 8.12 fim da raiz X espaço menor que raiz quadrada de 96$

De fato, a raiz quadrada aproximada de 96 é 9,79. Concluímos que a capacidade X do tanque é menor que 10 mil litros.

Exercício 7

(Aeronáutica 2021) Seja a P.G. (24, 36, 54, ...). Ao somar o 5º e o 6º termos dessa P.G. tem-se

a) 81/2
b) 405/2
c) 1215/4
d) 1435/4

Ver Resposta

Resposta correta: c) 1215/4

Objetivo
Somar a5 + a6

Resolução

Passo 1: determinar a razão q.

A razão da PG é:

$q igual a a com 2 subscrito sobre a com 1 subscrito igual a 36 sobre 24 igual a 3 sobre 2$

Passo 2: determinar a5

a4 = a3 . q
a5 = a4 . q

Substituindo a4 em a5:

$a com 5 subscrito espaço igual a espaço a com 3 subscrito espaço. espaço q espaço. espaço q espaço igual a espaço a com 3 subscrito espaço. espaço q ao quadrado$

Passo 3: determinar a6

a6 = a5 . q

Substituindo a5 em a6:

$a com 6 subscrito igual a a com 5 subscrito espaço. espaço q espaço igual a espaço a com 3 subscrito espaço. espaço q ao quadrado espaço. espaço q espaço igual a espaço a com 3 subscrito espaço. espaço q ao cubo$

Passo 4: somar a5 + a6 substituindo os valores numéricos.

$a com 5 subscrito mais a com 6 subscrito igual a a com 3 subscrito. q ao quadrado espaço mais espaço a com 3 subscrito. q ao cubo a com 5 subscrito mais a com 6 subscrito igual a 54 espaço. espaço abre parênteses 3 sobre 2 fecha parênteses ao quadrado mais espaço 54 espaço. espaço abre parênteses 3 sobre 2 fecha parênteses ao cubo a com 5 subscrito mais a com 6 subscrito igual a 54 espaço. espaço 9 sobre 4 espaço mais espaço 54 espaço. espaço 27 sobre 8$

Colocando 54 em evidência:

$a com 5 subscrito mais a com 6 subscrito igual a 54 espaço abre parênteses 9 sobre 4 espaço mais espaço 27 sobre 8 fecha parênteses a com 5 subscrito mais a com 6 subscrito igual a 54 abre parênteses numerador 9 espaço. espaço 8 sobre denominador 4 espaço. espaço 8 fim da fração mais espaço numerador 27 espaço. espaço 4 sobre denominador 4 espaço. espaço 8 fim da fração fecha parênteses a com 5 subscrito mais a com 6 subscrito igual a 54 abre parênteses 72 sobre 32 mais 108 sobre 32 fecha parênteses a com 5 subscrito mais a com 6 subscrito igual a 54 abre parênteses 180 sobre 32 fecha parênteses a com 5 subscrito mais a com 6 subscrito igual a 54 espaço. espaço 180 sobre 32 igual a 9720 sobre 32 igual a 1215 sobre 4$

Exercício 8

(UERJ 2019) Os triângulos A1B1C1, A2B2C2, A3B3C3, ilustrados abaixo, possuem perímetros p1, p2, p3, respectivamente. Os vértices desses triângulos, a partir do segundo, são os pontos médios dos lados do triângulo anterior.

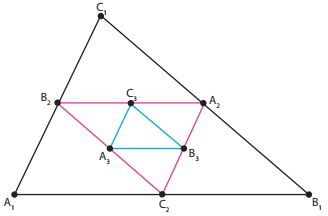
Admita que $pilha A com 1 subscrito B com 1 subscrito com barra acima igual a pilha B com 1 subscrito C com 1 subscrito com barra acima igual a 7 espaço e espaço pilha A com 1 subscrito C com 1 subscrito com barra acima igual a 4$ .

Assim, (p1, p2, p3) define a seguinte progressão:

a) aritmética de razão = – 8
b) aritmética de razão = – 6
c) geométrica de razão = 1/2
d) geométrica de razão = 1/4

Ver Resposta

Resposta correta: c) geométrica de razão = 1/2

Resolução

Passo 1: definir os perímetro p1, p2 e p3.

$p com 1 subscrito igual a espaço pilha A com 1 subscrito B com 1 subscrito com barra acima mais espaço pilha B com 1 subscrito C com 1 subscrito com barra acima mais pilha A com 1 subscrito C com 1 subscrito com barra acima p com 1 subscrito igual a 7 espaço mais espaço 7 espaço mais espaço 4 p com 1 subscrito igual a 18$

Por paralelismo, verificamos que os lados do triângulo interior, são a metade do imediatamente exterior.

Por exemplo, B2A2 = A1C2

Desta forma, p2 é a metade de p1, assim como, p3 é a metade de p2. Temos:

$p com 2 subscrito igual a p com 1 subscrito dividido por 2 igual a 9 e p com 3 subscrito igual a p com 2 subscrito dividido por 2 igual a 9 espaço dividido por 2 igual a 4 vírgula 5$

Passo 2: montar a progressão e classificá-la.

$p com 1 subscrito vírgula espaço p com 2 subscrito vírgula espaço p com 3 subscrito espaço igual a espaço 18 vírgula espaço 9 vírgula espaço 4 vírgula 5$

Verifica-se que, para determinar p2, 18 é multiplicado por 1/2.

$18 espaço sinal de multiplicação espaço 1 meio igual a 9$

Também, 9 multiplicado por 1/2 é 4,5.

$9 espaço sinal de multiplicação espaço 1 meio igual a 9 sobre 2 igual a 4 vírgula 5$

Conclusão
Verificamos que a progressão é geométrica, com razão 1/2.

Exercício 9

(Enem 2021) O gráfico informa a produção registrada por uma indústria nos meses de janeiro, março e abril.

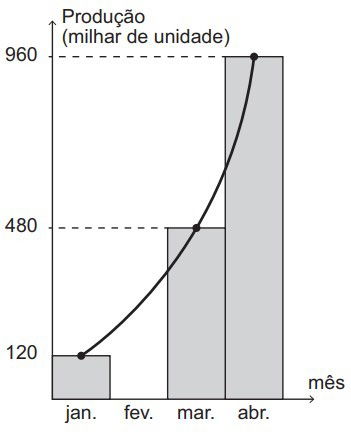
Por problemas logísticos, não foi feito o levantamento sobre a produção do mês de fevereiro. Entretanto, as informações dos outros três meses sugerem que a produção nesse quadrimestre cresceu exponencialmente, conforme aponta a curva de tendência traçada no gráfico.

Assumindo a premissa de que o crescimento nesse período foi exponencial, pode-se inferir que a produção dessa indústria no mês de fevereiro, em milhar de unidade, foi

a) 0.
b) 120.
c) 240.
d) 300.
e) 400.

Ver Resposta

Reposta correta: c) 240.

Resolução

O termo geral de uma PG é uma uma exponencial em função de n, onde a1 e q são números constantes.

$a com n subscrito igual a a com 1 subscrito espaço. espaço q à potência de n menos 1 fim do exponencial$

a1 = 120

A razão q, pode ser determinada por a4 / a3, assim:

$q espaço igual a espaço a com 4 subscrito sobre a com 3 subscrito igual a 960 sobre 480 igual a 2$

A quantidade de fevereiro é a2, que é obtido multiplicando a1 por q.

$a com 2 subscrito igual a 120 espaço. espaço q a com 2 subscrito igual a 120 espaço. espaço 2 espaço igual a espaço 240$

Portanto, a produção no mês de fevereiro foi de 240.

Continue praticando com:

Veja também:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações