Expressões Algébricas

Rosimar Gouveia

Professora de Matemática e Física

Expressões algébricas são expressões matemáticas que apresentam números, letras e operações.

As expressões desse tipo são usadas com frequência em fórmulas e equações.

As letras que aparecem em uma expressão algébrica são chamadas de variáveis e representam um valor desconhecido.

Os números escritos na frente das letras são chamados de coeficientes e deverão ser multiplicados pelos valores atribuídos as letras.

Exemplos

a) x + 5
b) b² – 4ac

Cálculo de uma Expressão Algébrica

O valor de uma expressão algébrica depende do valor que será atribuído às letras.

Para calcular o valor de uma expressão algébrica devemos substituir os valores das letras e efetuar as operações indicadas. Lembrando que entre o coeficiente e a letras, a operação é de multiplicação.

Exemplo

O perímetro de um retângulo é calculado usando a fórmula:

P = 2b + 2h

Substituindo as letras com os valores indicados, encontre o perímetro dos seguintes retângulos

Para saber mais sobre perímetro leia também Perímetro de figuras planas.

Simplificação de Expressões Algébricas

Podemos escrever as expressões algébricas de forma mais simples somando seus termos semelhantes (mesma parte literal).

Para simplificar iremos somar ou subtrair os coeficientes dos termos semelhantes e repetir a parte literal.

Exemplos

a) 3xy + 7xy⁴ - 6x³y + 2xy - 10xy⁴ = (3xy + 2xy) + (7xy⁴ - 10xy⁴) - 6x³y = 5xy - 3xy⁴ - 6x³y
b) ab - 3cd + 2ab - ab + 3cd + 5ab = (ab + 2ab - ab + 5ab) + (- 3cd + 3cd) = 7ab

Fatoração de Expressões Algébricas

Fatorar significa escrever uma expressão como produto de termos.

Transformar uma expressão algébrica em uma multiplicação de termos, frequentemente nos permite simplificar a expressão.

Para fatorar uma expressão algébrica podemos usar os seguintes casos:

Fator comum em evidência: ax + bx = x . (a + b)

Agrupamento: ax + bx + ay + by = x . (a + b) + y . (a + b) = (x + y) . (a + b)

Trinômio Quadrado Perfeito (Adição): a² + 2ab + b² = (a + b)²

Trinômio Quadrado Perfeito (Diferença): a² – 2ab + b² = (a – b)²

Diferença de dois quadrados: (a + b) . (a – b) = a² – b²

Cubo Perfeito (Soma): a³ + 3a²b + 3ab² + b³ = (a + b)³

Cubo Perfeito (Diferença): a³ - 3a²b + 3ab² - b³ = (a - b)³

Para saber mais sobre fatoração, leia também:

• Polinômios
• Fatoração de Polinômios
• Produtos Notáveis - Exercícios

Monômios

Quando uma expressão algébrica apresenta apenas multiplicações entre o coeficiente e as letras (parte literal), ela é chamada de monômio.

Exemplos

a) 3ab
b) 10xy²z³
c) bh (quando não aparece nenhum número no coeficiente, seu valor é igual a 1)

Os monômios semelhantes são os que apresentam a mesma parte literal (mesmas letras com mesmos expoentes).

Os monômios 4xy e 30xy são semelhantes. Já os monômios 4xy e 30x²y³ não são semelhantes, pois as letras correspondentes não possuem o mesmo expoente.

Polinômios

Quando uma expressão algébrica possui somas e subtrações de monômios não semelhantes é chamada de polinômio.

Exemplos

a) 2xy + 3 x²y - xy³
b) a + b
c) 3abc + ab + ac + 5 bc

Operações Algébricas

Soma e subtração

A soma ou a subtração algébrica é feita somando-se ou subtraindo-se os coeficientes dos termos semelhantes e repetindo a parte literal.

Exemplo

a) Somar (2x² + 3xy + y²) com (7x² - 5xy - y²)

(2x² + 3xy + y²) + (7x² - 5xy - y²) = (2 + 7) x² + (3 - 5) xy + (1 - 1) y² = 9x² - 2xy

b) Subtrair (5ab - 3bc + a²) de (ab + 9bc - a³)

É importante observar que o sinal de menos na frente dos parênteses inverte todos os sinais de dentro dos parênteses.

(5ab - 3bc + a²) - (ab + 9bc - a³) = 5ab - 3bc + a² - ab - 9bc + a³ =
(5 - 1) ab + (- 3 - 9)bc + a² + a³ = 4ab -12bc + a² + a³

Multiplicação

A multiplicação algébrica é feita multiplicando-se termo a termo.

Para multiplicar a parte literal, usamos a propriedade da potenciação para multiplicação de mesma base: "repete-se a base e soma-se os expoentes".

Exemplo

Multiplicar (3x² + 4xy) com (2x + 3)

(3x² + 4xy) . (2x + 3) = 3x² . 2x + 3x² . 3 + 4xy . 2x + 4xy . 3 = 6x³ + 9x² + 8x²y + 12xy

Divisão de um polinômio por um monômio

A divisão de um polinômio por um monômio é feita dividindo os coeficientes do polinômio pelo coeficiente do monômio. Na parte literal, usa-se a propriedade da divisão de potência de mesma base (repete-se a base e subtrai os expoentes).

Exemplo

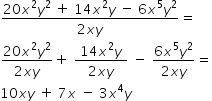
Para saber mais, leia também:

• Expressões Numéricas
• Produtos Notáveis
• Equação do 1º Grau

Exercícios

1) Sendo a = 4 e b = - 6, encontre o valor numérico das seguintes expressões algébricas:

a) 3a + 5b
b) a² - b
c) 10ab + 5a² - 3b

2) Escreva uma expressão algébrica para expressar o perímetro da figura abaixo:

3) Simplifique os polinômios:

a) 8xy + 3xyz - 4xyz + 2xy
b) a + b + ab + 5b + 3ab + 9a - 5c
c) x³ + 10x² + 5x - 8x² - x³

4) Sendo,

A = x - 2y
B = 2x + y
C = y + 3

Calcule:

a) A + B
b) B - C
c) A . C

5) Qual o resultado da divisão do polinômio 18x⁴ + 24x³ - 6x² + 9x pelo monômio 3x?

Confira mais questões, com resolução comentada, em:

• Exercícios de fatoração de polinômios resolvidos
• Exercícios sobre Expressões Algébricas
• Exercícios de polinômios: adição e subtração

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.