Fatorial: como calcular, exemplos e exercícios

Fatorial é um número natural inteiro positivo, o qual é representado por n!

O fatorial de um número é calculado pela multiplicação desse número por todos os seus antecessores até chegar ao número 1. Note que nesses produtos, o zero (0) é excluído.

O fatorial é representado por:

n! = n . (n – 1) . (n – 2) . ... . (n – (n-1))!

Exemplos de números fatoriais

Fatorial de 0: 0! (lê-se 0 fatorial)

0! = 1

Fatorial de 1: 1! (lê-se 1 fatorial)

1! = 1

Fatorial de 2: 2! (lê-se 2 fatorial)

2! = 2 . 1 = 2

Fatorial de 3: 3! (lê-se 3 fatorial)

3! = 3 . 2 . 1 = 6

Fatorial de 4: 4! (lê-se 4 fatorial)

4! = 4. 3 . 2 . 1 = 24

Fatorial de 5: 5! (lê-se 5 fatorial)

5! = 5 . 4 . 3 . 2 . 1 = 120

Fatorial de 6: 6! (lê-se 6 fatorial)

6! = 6 . 5 . 4 . 3 . 2 . 1 = 720

Fatorial de 7: 7! (lê-se 7 fatorial)

7! = 7 . 6 . 5 . 4. 3 . 2 . 1 = 5040

Fatorial de 8: 8! (lê-se 8 fatorial)

8! = 8 . 7 . 6 . 5 . 4. 3 . 2 . 1 = 40320

Fatorial de 9: 9! (lê-se 9 fatorial)

9! = 9 . 8 . 7 . 6 . 5 . 4. 3 . 2 . 1 = 362.880

Fatorial de 10: 10! (lê-se 10 fatorial)

10! = 10 . 9 . 8 . 7 . 6 . 5 . 4. 3 . 2 . 1 = 3.628.800

Obs: O número fatorial também pode ser representado da seguinte maneira:

5!
5 . 4!;
5 . 4 . 3!;
5 . 4 . 3 . 2!

Esse processo é muito importante quando se utiliza a simplificação de números fatoriais.

Fatorial e Análise Combinatória

Os números fatoriais estão intimamente relacionados com os tipos de análise combinatória. Isso porque ambos envolvem a multiplicação de números naturais consecutivos.

Arranjos

Combinações

Permutações

Aprenda mais sobre análise combinatória.

Equação de Fatorial

Na matemática, há equações onde os números fatoriais estão presentes, por exemplo:

x – 10 = 4!
x – 10 = 24
x = 24+10
x = 34

Operações com Fatoriais

Adição

3! + 2!
(3 . 2 . 1) + (2 . 1)
6 + 2 = 8

Subtração

5! - 3!
(5 . 4 . 3 . 2 . 1) – (3 . 2 . 1)
120 – 6 = 114

Multiplicação

0! . 6!
1 . (6 . 5. 4 . 3 . 2 . 1)
1 . 720 = 720

Divisão

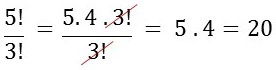
Simplificação de Fatorial

Na divisão de números fatoriais o processo de simplificação é um dos mais importantes:

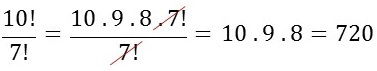
Análise Fatorial

A análise fatorial é um método utilizado nos estudos de estatísticas por meio da criação de variáveis. No campo da psicologia ela também é explorada no desenvolvimento de instrumentos psicológicos.

Leia também sobre

• Permutação
• Arranjo na matemática: o que é, como calcular, exemplos
• Combinação na matemática: como calcular e exemplos
• Princípio fundamental da contagem
• Binômio de Newton
• Exercícios de Análise Combinatória

Exercícios de fatorial com respostas

Exercício 1

(UFF) O produto 20 x 18 x 16 x 14 x ... x 6 x 4 x 2 é equivalente a:

a)
b)
c)
d)
e)

Exercício 2

(PUC-RS) Se 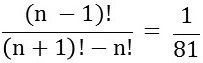, então n é igual a:

a) 13
b) 11
c) 9
d) 8
e) 6

Exercício 3

(UNIFOR) A soma de todos os números primos que são divisores de 30! é :

a) 140
b) 139
c) 132
d) 130
e) 129

Veja também:

Exercícios de permutação resolvidos e explicados