Função Polinomial: o que é, seus tipos e gráficos

Rafael C. Asth

Professor de Matemática e Física

As funções polinomiais são definidas por expressões polinomiais. Elas são representadas pela expressão:

onde,

• n: número inteiro positivo ou nulo
• x: variável
• a₀, a₁, ... a_{n – 1}, a_n são os coeficientes

Os termos são:

• a_n . x_n,
• a_{n – 1} . x_{n – 1,}
• ... a₁ . x,
• a₀:

Cada função polinomial associa-se a um único polinômio, sendo assim, chamamos as funções polinomiais também de polinômios.

Um polinômio é uma sequência de somas e/ou subtrações de monômios, termos formados por números e letras. Nos monômios, as letras e números estão conectados por multiplicações e divisões.

Exemplos de monômios:

Monômio	coeficiente	variável
	1
	4

Um possível polinômio formado pelos monômios anteriores seria:

Ao polinômio anterior, podemos associar uma função polinomial.

Esta expressão nos diz que para cada valor de x, há um respectivo valor para f(x).

Valor Numérico de um Polinômio

Para encontrar o valor numérico de um polinômio, substituímos um valor numérico na variável x.

Exemplo

Qual o valor numérico de p(x) = 2x³ + x² - 5x - 4 para x = 3?

Substituindo o valor na variável x temos:

Grau de uma função polinomial

Dependendo do expoente mais elevado que apresentam em relação à variável, os polinômios são classificados em:

• Função polinomial de grau 1: f(x) = x + 6
• Função polinomial de grau 2: g(x) = 2x² + x - 2
• Função polinomial de grau 3: h(x) = 5x³ + 10x² - 6x + 15
• Função polinomial de grau 4: p(x) = 20x⁴ - 15x³+ 5x² + x - 10
• Função polinomial de grau 5: q(x) = 25x⁵ + 12x⁴ - 9x³ + 5x² + x - 1

Obs: o polinômio nulo é aquele que possui todos os coeficientes iguais a zero. Quando isso ocorre, o grau do polinômio não é definido.

Gráficos da Função Polinomial

Podemos associar um gráfico a uma função polinomial, atribuindo valores a x na expressão p(x).

Desta forma, encontraremos os pares ordenados (x,y), que serão pontos pertencentes ao gráfico.

Ligando esses pontos teremos o esboço do gráfico da função polinomial.

Veja alguns exemplos de gráficos:

Função polinomial de grau 1

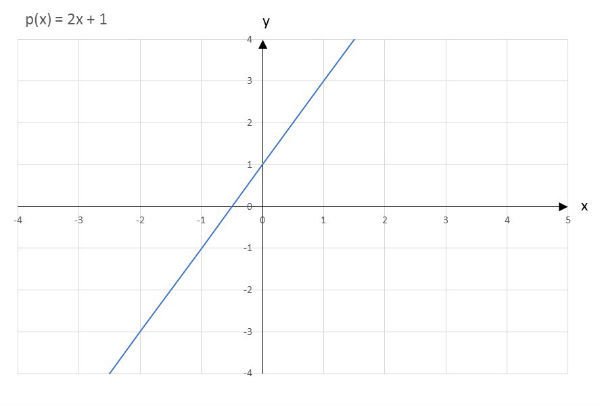
Função polinomial de grau 2

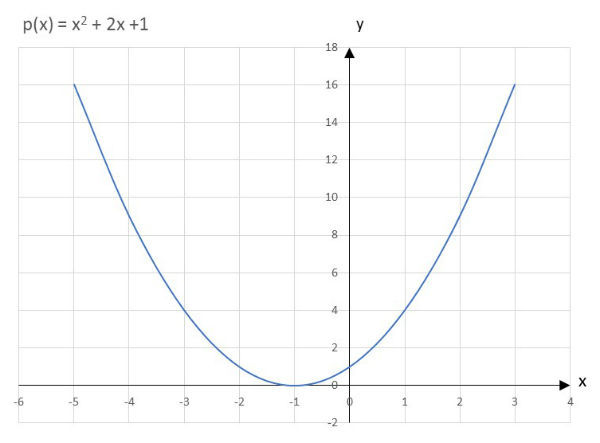
Função polinomial de grau 3

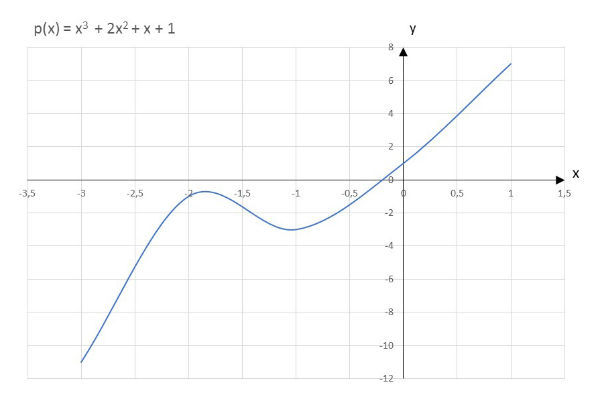
Igualdade de Polinômios

Dois polinômios são iguais se os coeficientes dos termos de mesmo grau são todos iguais.

Exemplo
Determine o valor de a, b, c e d para que os polinômios:

p(x) = ax⁴ + 7x³ + (b + 10)x² - c

e

h(x) = (d + 4)x³ + 3bx² + 8.

Para os polinômios serem iguais é necessário que os coeficientes correspondentes sejam iguais.

Então,

a = 0 (o polinômio h(x) não tem o termo x⁴, sendo assim seu valor é igual a zero)
b + 10 = 3b → 2b = 10 → b = 5
- c = 8 → c = - 8
d + 4 = 7 → d = 7 - 4 → d = 3

Operações com Polinômios

Confira abaixo exemplos das operações entre polinômios:

Adição

(- 7x³ + 5x² - x + 4) + (- 2x² + 8x -7)
- 7x³ + 5x² - 2x² - x + 8x + 4 - 7
- 7x³ + 3x² + 7x -3

Subtração

(4x² - 5x + 6) - (3x - 8)
4x² - 5x + 6 - 3x + 8
4x² - 8x + 14

Multiplicação

(3x² - 5x + 8) . (- 2x + 1)
- 6x³ + 3x² + 10x² - 5x - 16x + 8
- 6x³ + 13x² - 21x + 8

Divisão

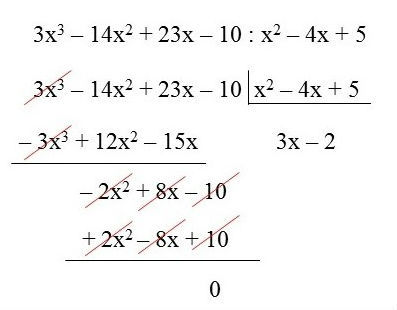
Obs: Na divisão de polinômios utilizamos o método chave. Primeiramente realizamos a divisão entre os coeficientes numéricos e depois a divisão de potências de mesma base. Para isso, conserva-se a base e subtraia os expoentes.

A divisão é formada por: dividendo, divisor, quociente e resto.

divisor . quociente + resto = dividendo

Teorema do Resto

O Teorema do Resto representa o resto na divisão dos polinômios e possui o seguinte enunciado:

O resto da divisão de um polinômio f(x) por x - a é igual a f(a).

Leia também:

• Polinômios
• Fatoração de Polinômios
• Função Quadrática
• Função Exponencial
• Função Afim
• Exercícios de polinômios: adição e subtração

Exercícios de função polinomial

Exercício 1

(Cefet-MG) O polinômio P(x) é divisível por x - 3. Dividindo-se P(x) por x - 1, obtém-se o quociente Q(x) e resto 10. Nessas condições, o resto da divisão de Q(x) por x - 3 vale:

a) - 5
b) - 3
c) 0
d) 3
e) 5

Exercício 2

(UF-PB) Na inauguração da praça, foram realizadas várias atividades recreativas e culturais. Dentre elas, no anfiteatro, um professor de Matemática proferiu uma palestra para vários alunos do ensino médio e propôs o seguinte problema: Encontrar valores para a e b, de modo que o polinômio p(x) = ax³ + x² + bx + 4 seja divisível por
q(x) = x² - x - 2. Alguns alunos resolveram corretamente esse problema e, além disso, constataram que a e b satisfazem a relação:

a) a² + b² = 73
b) a² - b² = 33
c) a + b = 6
d) a² + b = 15
e) a - b= 12

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.