Funções Trigonométricas

Rafael C. Asth

Professor de Matemática e Física

As funções trigonométricas, também chamadas de funções circulares, estão relacionadas com as demais voltas no ciclo trigonométrico.

As principais funções trigonométricas são:

• Função Seno
• Função Cosseno
• Função Tangente

No círculo trigonométrico temos que cada número real está associado a um ponto da circunferência.

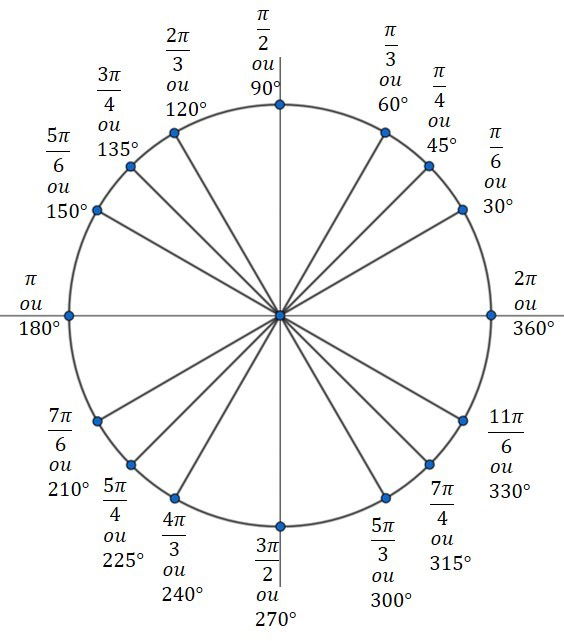
Figura do Círculo Trigonométrico dos ângulos expressos em graus e radianos

Funções Periódicas

As funções periódicas são funções que possuem um comportamento periódico. Ou seja, que ocorrem em determinados intervalos de tempo.

O período corresponde ao menor intervalo de tempo em que acontece a repetição de determinado fenômeno.

Uma função f: A → B é periódica se existir um número real positivo p tal que

f(x) = f (x+p), ∀ x ∈ A

O menor valor positivo de p é chamado de período de f.

Note que as funções trigonométricas são exemplos de funções periódicas visto que apresentam certos fenômenos periódicos.

Função Seno

A função seno é uma função periódica e seu período é 2π. Ela é expressa por:

f(x) = sen x

No círculo trigonométrico, o sinal da função seno é positivo quando x pertence ao primeiro e segundo quadrantes. Já no terceiro e quarto quadrantes, o sinal é negativo.

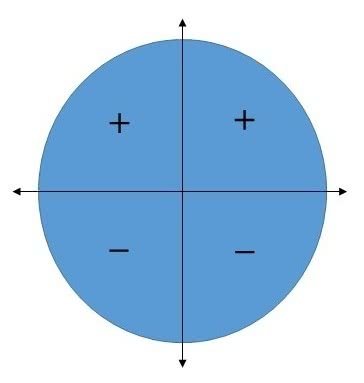
Além disso, no primeiro e quarto quadrantes a função f é crescente. Já no segundo e terceiro quadrantes a função f é decrescente.

O domínio e o contradomínio da função seno são iguais a R. Ou seja, ela está definida para todos os valores reais: Dom(sen)=R.

Já o conjunto da imagem da função seno corresponde ao intervalo real [-1, 1]: -1 < sen x < 1.

Em relação à simetria, a função seno é uma função ímpar: sen(-x) = -sen(x).

O gráfico da função seno f(x) = sen x é uma curva chamada de senoide:

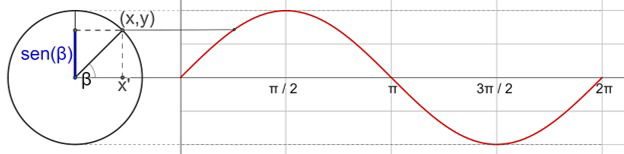
Gráfico da função seno

Leia também: Lei dos Senos.

Função Cosseno

A função cosseno é uma função periódica e seu período é 2π. Ela é expressa por:

f(x) = cos x

No círculo trigonométrico, o sinal da função cosseno é positivo quando x pertence ao primeiro e quarto quadrantes. Já no segundo e terceiro quadrantes, o sinal é negativo.

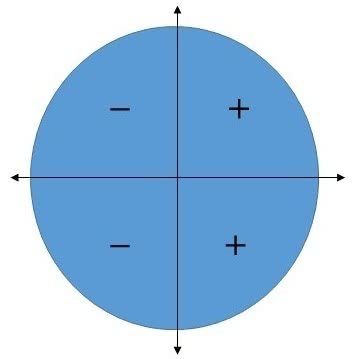
Além disso, no primeiro e segundo quadrantes a função f é decrescente. Já no terceiro e quarto quadrantes a função f é crescente.

O domínio e o contradomínio da função cosseno são iguais a R. Ou seja, ela está definida para todos os valores reais: Dom(cos)=R.

Já o conjunto da imagem da função cosseno corresponde ao intervalo real [-1, 1]: -1 < cos x < 1.

Em relação à simetria, a função cosseno é uma função par: cos(-x) = cos(x).

O gráfico da função cosseno f(x) = cos x é uma curva chamada de cossenoide:

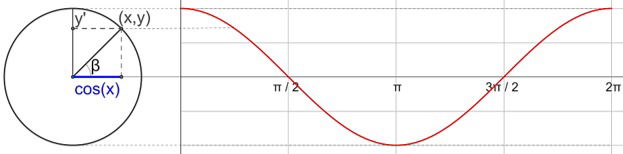Gráfico da função cosseno

Leia também: Lei dos Cossenos.

Função Tangente

A função tangente é uma função periódica e seu período é π. Ela é expressa por:

f(x) = tg x

No círculo trigonométrico, o sinal da função tangente é positiva quando x pertence ao primeiro e terceiro quadrantes. Já no segundo e quarto quadrantes, o sinal é negativo.

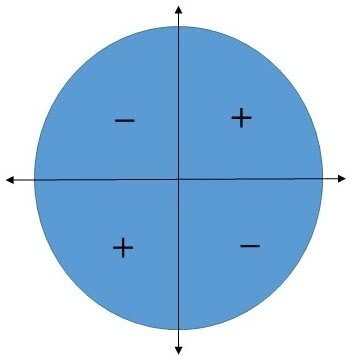
Além disso, a função f definida por f(x) = tg x é sempre crescente em todos os quadrantes do círculo trigonométrico.

O domínio da função tangente é: Dom(tan)={x ∈ R│x ≠ de π/2 + kπ; K ∈ Z}. Assim, não definimos tg x, se x = π/2 + kπ.

Já o conjunto da imagem da função tangente corresponde a R, ou seja, o conjunto dos números reais.

Em relação à simetria, a função tangente é uma função ímpar: tg(-x) = -tg(x).

O gráfico da função tangente f(x) = tg x é uma curva chamada de tangentoide:

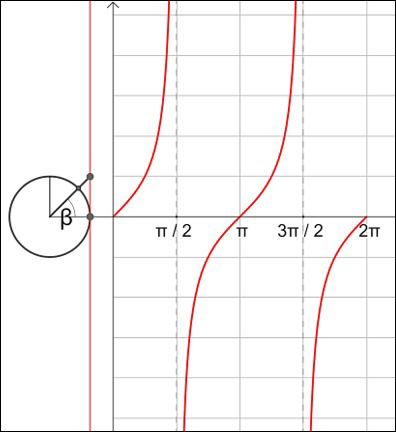
Gráfico da função tangente

Leia mais sobre o tema:

• Seno, Cosseno e Tangente
• Exercícios de seno, cosseno e tangente
• Relações Trigonométricas
• Trigonometria
• Trigonometria no Triângulo Retângulo
• Exercícios de Trigonometria no triângulo retângulo
• Círculo Trigonométrico
• Razões Trigonométricas
• Identidades trigonométricas
• Tabela Trigonométrica
• Função Exponencial
• Função modular
• Fórmulas de Matemática
• O que é função
• Radiano: o que é e como e medir

Exercícios de funções trigonométricas

Exercício 1

(UFAM) O menor valor não negativo côngruo ao arco de rad é igual a:

a) π/5 rad
b) 7 π/5 rad
c) π rad
d) 9 π/5 rad
e) 2 π rad

Exercício 2

(Cefet-PR) A função real f(x) = a + b . sen cx tem imagem igual a [-7, 9] e seu período é π/2 rad. Assim, a + b + c vale:

a) 13
b) 9
c) 8
d) – 4
e) 10

Exercício 3

(UFPI) O período da função f(x) = 5 + sen (3x – 2) é:

a) 3π
b) 2π/3
c) 3π – 2
d) π/3 – 2
e) π/5

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.