Geometria espacial: quais são as figuras e suas fórmulas
A Geometria Espacial é a parte da matemática que estuda formas com três dimensões. Ela lida com objetos que ocupam espaço, como cubos e esferas. De modo geral, a Geometria Espacial pode ser definida como o estudo da geometria no espaço.
A geometria espacial é bastante utilizada em campos de estudo como: arquitetura, engenharia e design, onde é fundamental para projetar e construir estruturas, criar modelos tridimensionais e realizar cálculos precisos de volumes e áreas.
Além disso, a geometria espacial desempenha um papel importante em ciências naturais e engenharia, como na astronomia para mapear o espaço e na geologia para modelar terrenos. É fundamental em sistemas de navegação, como o GPS, para calcular posições e rotas, e também é aplicada em áreas como a medicina para criar imagens detalhadas do corpo humano.
Outro campo de estudo da geometria lida com figuras planas, como triângulos e círculos. A geometria plana estuda figuras com duas dimensões.
Neste conteúdo você encontra:
Características da geometria espacial
A Geometria Espacial estuda os objetos que possuem mais de duas dimensões e ocupam lugar no espaço. Por sua vez, esses objetos são conhecidos como “sólidos geométricos” ou “figuras geométricas espaciais”.
Dessa forma, a geometria espacial pode determinar, por meio de cálculos, o volume destes objetos, ou seja, o espaço ocupado por eles.
Contudo, o estudo das estruturas das figuras espaciais e suas inter-relações é determinado por alguns conceitos básicos, a saber:
- Ponto: conceito fundamental a todos os subsequentes, uma vez que todos sejam, em última análise, formados por inúmeros pontos. Por sua vez, os pontos são infinitos e não possuem dimensão mensurável (adimensional). Portanto, sua única propriedade garantida é sua localização.
- Reta: composta por pontos, é infinita nos dois lados e determina a distância mais curta entre dois pontos determinados.
- Linha: possui algumas semelhanças com a reta, ao ser igualmente infinita para cada lado, contudo, têm a propriedade de formar curvas e nós sobre si.
- Plano: é outra estrutura infinita que se estende em todas as direções.
Figuras geométricas espaciais
Segue abaixo alguns dos sólidos geométricos mais conhecidos:
Cubo
O cubo é um hexaedro regular composto de 6 faces quadradas, 12 arestas e 8 vértices.
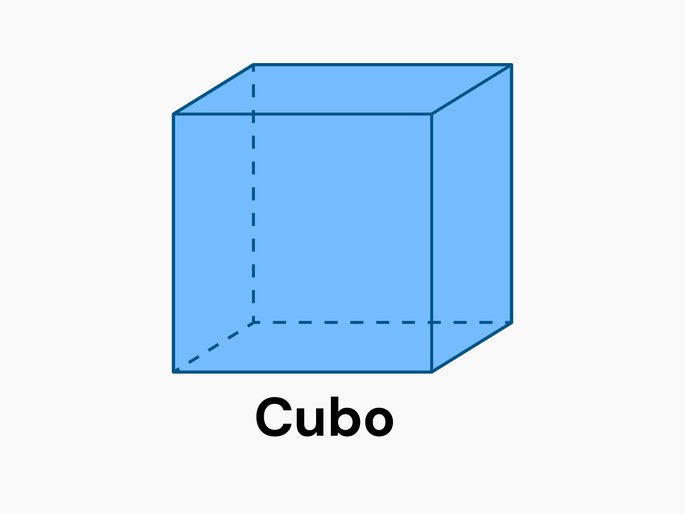
Sendo a a medida da aresta:
Volume do cubo
Área lateral do cubo
Área total do cubo
Aprofunde os seus conhecimentos sobre cubo.
Paralelepípedo
O paralelepípedo é formado por 6 faces retangulares, 12 arestas e 8 vértices. Diferente do cubo, as medidas das arestas do comprimento, da largura e da altura, não possuem necessariamente a mesma medida.
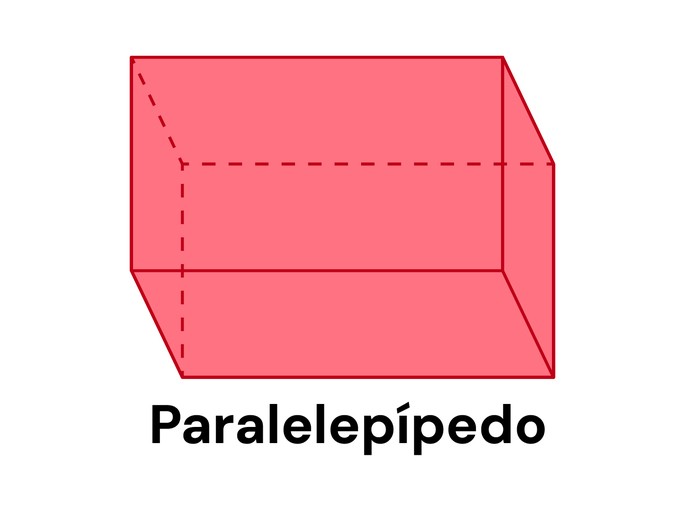
Sendo: L a medida da largura, c do comprimento e a da altura.
Volume do paralelepípedo
Área total do paralelepípedo
Prisma
O Prisma é um poliedro composto por duas faces paralelas que formam as bases, que por sua vez, podem ser triangulares, quadrangulares, pentagonais, hexagonais ou, qualquer outro polígono.
Além das bases, o prima é composto de altura, lados, vértices e arestas unidos por paralelogramos. De acordo com sua inclinação, os prismas podem ser retos, aqueles onde a aresta e a base fazem um ângulo de 90°, ou os oblíquos, compostos de ângulos diferentes de 90°.
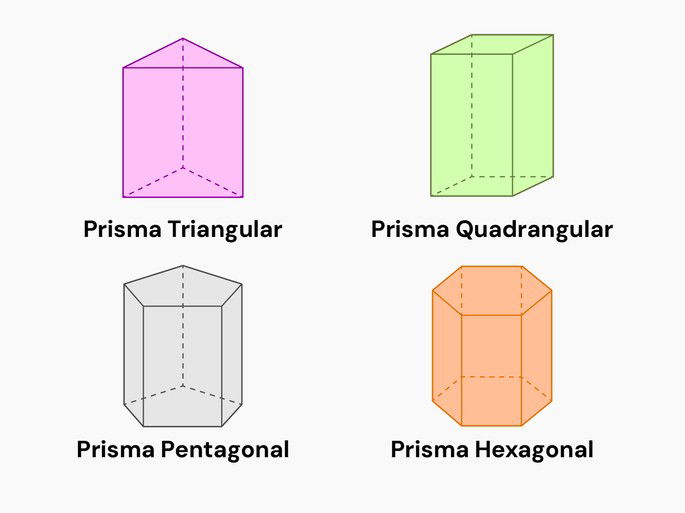
Volume do prisma
O volume de todo prisma é a multiplicação entre a medida de sua área da base pela sua altura (h).
A altura h do prisma é a distância entre suas bases.
Área do prisma
O cálculo da área da base depende do polígono que forma suas bases. Já a área lateral é a soma das áreas dos retângulos que formam sua lateral.
Prisma triangular
É o prisma cujas bases são triângulos.
No caso particular em que a base é um triângulo equilátero, temos:
Volume:
Área total:
Onde:
é a medida da aresta da base e h é a altura do prisma.
Prisma hexagonal
É o prisma onde a base é um hexágono.
No caso particular onde a base é um hexágono regular, temos:
Volume
Área lateral
Área das bases (das duas juntas)
Aprenda mais sobre Prisma e o Volume do Prisma.
Pirâmide
A pirâmide é um poliedro composto por uma base (triangular, pentagonal, quadrada, retangular, paralelogramo) e um vértice (vértice da pirâmide) que une todas as faces laterais triangulares.
Sua altura corresponde a distância entre o vértice e sua base. Quanto à sua inclinação podem ser classificadas em retas (ângulo de 90°) ou oblíquas (ângulos diferentes de 90°).
Volume da pirâmide
De forma geral, o volume da pirâmide é calculado pela multiplicação entre a área da base e sua altura, dividindo o resultado por 3.
O cálculo da área da base depende do polígono que forma esta base.
Área da pirâmide
A medida da área da pirâmide é a soma da área de sua base mais sua lateral.
Vale lembrar que as laterais das pirâmides são formadas por triângulos.
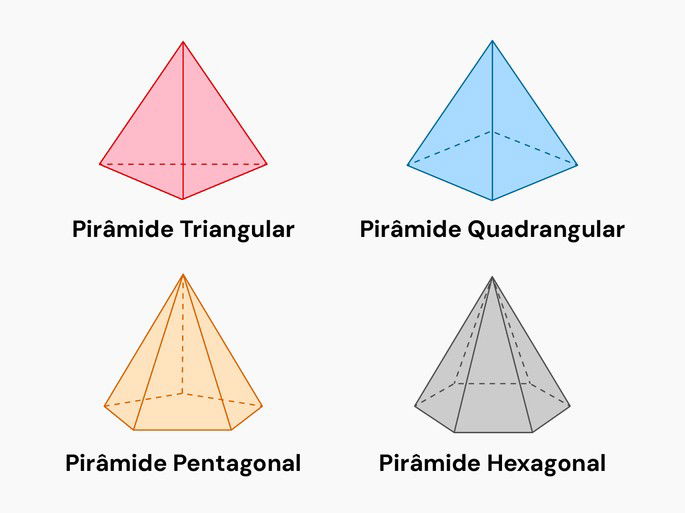
Aprenda mais sobre Pirâmide e Volume da Pirâmide.
Cilindro
O cilindro é uma forma espacial arredondada, por isso, não é considerado um poliedro. É formado por duas bases circulares e paralelas. A distância entre suas bases é sua altura.
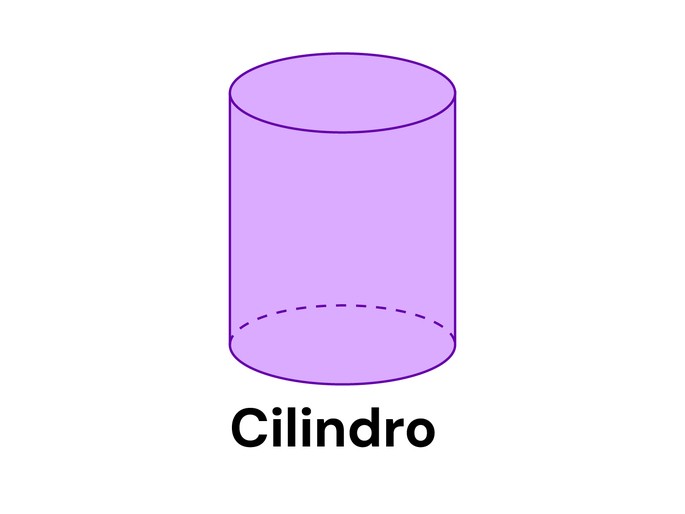
Sendo, r o raio da base e h a altura.
Volume do cilindro
Área do cilindro
A área total é formada pela soma das áreas das duas bases com sua área lateral.
Onde:
Esfera
A esfera é um sólido geométrico de forma arredondada, não sendo um poliedro.
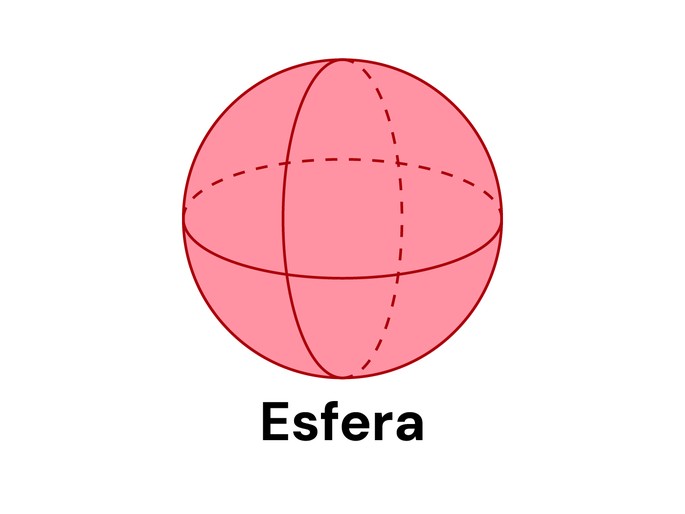
Volume da esfera
Área da esfera
Cone
O cone é um sólido de revolução formado por uma base circular e um ponto fora desta base. O ponto que não pertence ao plano da base é o vértice do cone.
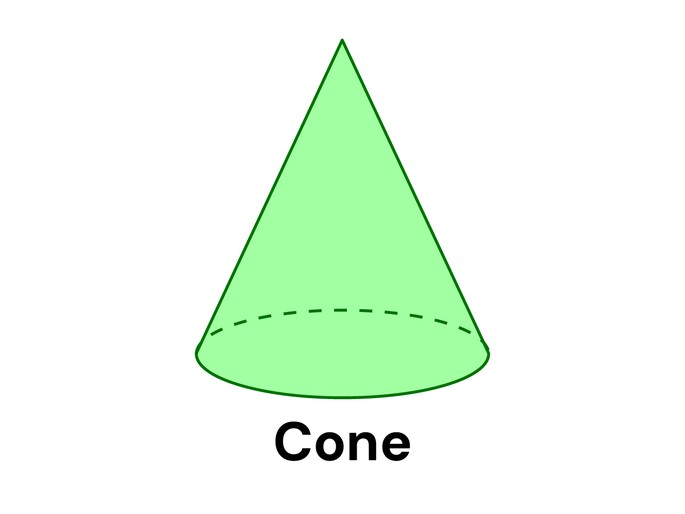
Sendo, r o raio da base e h a altura e g a geratriz.
Volume do cone
Área da lateral do cone
Área da base do cone
Aprofunde os seus conhecimentos também sobre Geometria Plana.
Sólidos de Platão
Os sólidos platônicos são poliedros especias, eles são formados por faces iguais. Todas as faces destes sólidos são polígonos regulares.
Tetraedro
O Tetraedro é um poliedro regular composto de 4 faces triangulares, 6 arestas e 4 vértices.
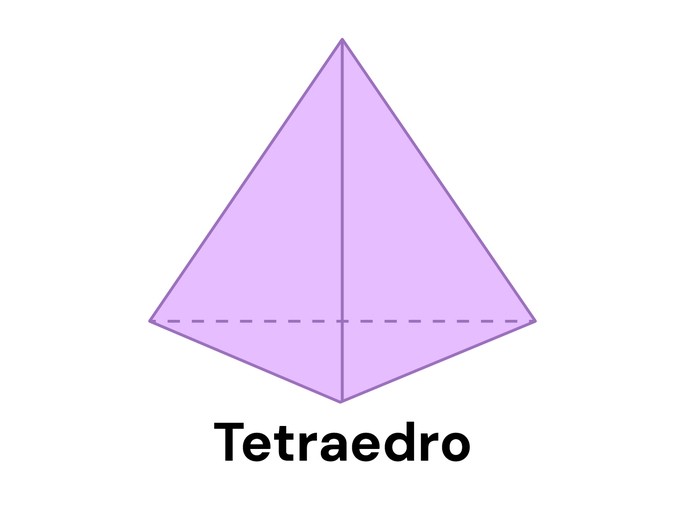
Volume do tetraedro
Área total do tetraedro
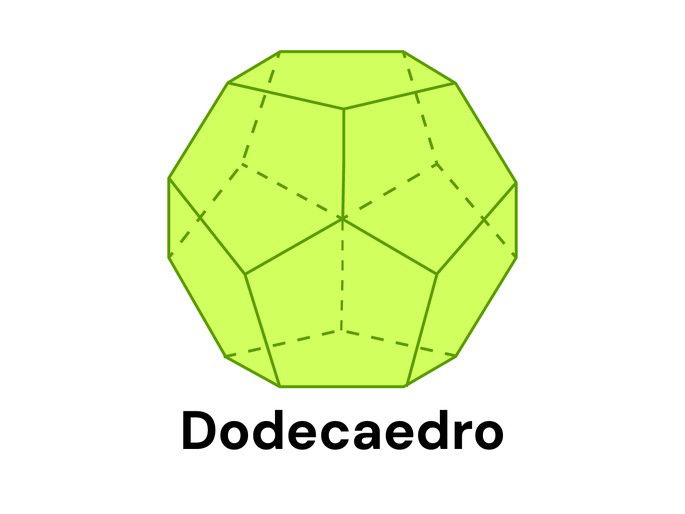
Dodecaedro
O Dodecaedro é um poliedro regular composto de 12 faces pentagonais regulares, 30 arestas e 20 vértices.
Volume do dodecaedro
Aproximadamente, o volume do dodecaedro é:
Área total do dodecaedro
Aproximadamente, a área do dodecaedro é:
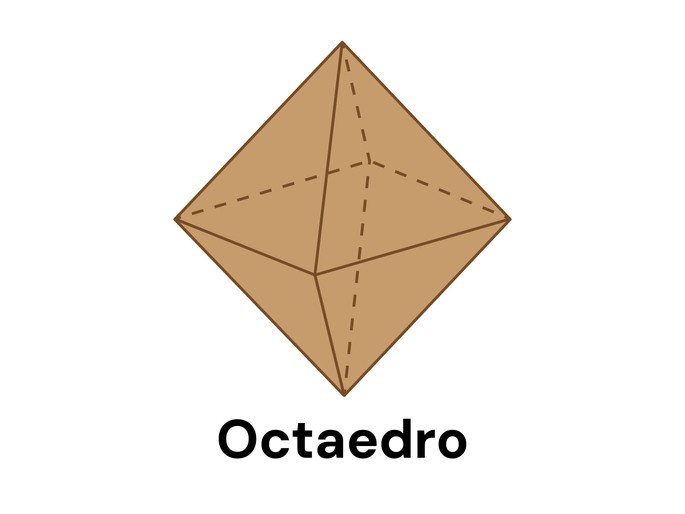
Octaedro
O Octaedro é um poliedro regular de 8 faces triangulares, sendo todas triângulos equiláteros. Ele possui 12 arestas congruentes e 6 vértices.
Volume do octaedro
Aproximadamente, o volume do octaedro é:
Área do octaedro
Aproximadamente, a área do octaedro é:
Icosaedro
O Icosaedro é um poliedro convexo composto de 20 faces triangulares, 30 arestas e 12 vértices.

Volume do Icosaedro
Aproximadamente, o volume do icosaedro é:
Área do Icosaedro
Aproximadamente, a área do octaedro é:
Exercícios sobre geometria espacial
Exercício 1
Um aquário é aberto na parte de cima, com formato de paralelepípedo reto retangular e 60 cm de comprimento, 40 cm de largura e 30 cm de altura. Qual é a sua área total e seu volume, respectivamente?
a) 8400 cm² e 72000 cm³
b) 7200 cm² e 72000 cm³
c) 7200 cm² e 36000 cm³
d) 4800 cm² e 24000 cm³
e) 3200 cm² e 24000 cm³
Dados do problema:
- Comprimento (c): 60 cm
- Largura (l): 40 cm
- Altura (h): 30 cm
Cálculo da área total:
Como mencionamos anteriormente, a área total de um paralelepípedo é a soma das áreas de suas faces. No caso do aquário, consideremos apenas as cinco faces (desconsiderando a parte superior, que está aberta).
1. Identificar as faces:
- Frente e trás: São dois retângulos iguais com as dimensões comprimento e altura.
- Lados: São dois retângulos iguais com as dimensões largura e altura.
- Fundo: Um retângulo com as dimensões comprimento e largura.
2. Calcular a área de cada tipo de face:
Área da frente e de trás: 2 × (comprimento × altura) = 2 × (60 cm × 30 cm) = 3600 cm²
Área dos lados: 2 × (largura × altura) = 2 × (40 cm × 30 cm) = 2400 cm²
Área do fundo: comprimento × largura = 60 cm × 40 cm = 2400 cm²
3. Somar as áreas de todas as faces:
Área total = 3600 cm² + 2400 cm² + 2400 cm² = 8400 cm²
Portanto, a área total da superfície do aquário é de 8400 centímetros quadrados.
Cálculo do volume:
Fórmula para calcular o volume de um paralelepípedo:
Volume = comprimento × largura × altura
V = c × l × h
Substituindo os valores:
V = 60 cm × 40 cm × 30 cm
V = 72.000 cm³
Portanto, o volume do aquário é de 72000 centímetros cúbicos.
Conclusão:
O aquário possui uma área de 8400 cm² e volume de 72000 cm³.
Exercício 2
Curiosidades
- A palavra “geometria” vem do grego e corresponde a união dos termos “geo” de terra e “metria” de medida, que significa “medir terra”.
- Os cálculos mais comuns em Geometria espacial são para determinar o comprimento de curvas, áreas de superfícies e volumes de regiões sólidas.
- Outras figuras geométricas espaciais: cilindro, cone, esfera.
- Os “Sólidos Platônicos” são poliedros convexos conhecidos desde a antiguidade clássica. Os cinco “sólidos platônicos” são: tetraedro, cubo, octaedro, dodecaedro, icosaedro.
Aprofunde os seus estudos com:
- Sólidos Geométricos
- Relação de Euler: vértices, faces e arestas
- Volume do Cubo
- Formas Geométricas
- Geometria Plana
Pratique com:
- Exercícios de Geometria Espacial (com gabarito resolvido)
- Exercícios sobre cilindros (com questões resolvidas)
- Exercícios sobre poliedros.
GOUVEIA, Rosimar. Geometria espacial: quais são as figuras e suas fórmulas. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/geometria-espacial/. Acesso em:



