Hexágono

Rafael C. Asth

Professor de Matemática e Física

Hexágono é um polígono de seis lados e seis vértices, por isso, possui seis ângulos. O hexágono é uma figura plana, possui duas dimensões, formadas por uma linha poligonal fechada e simples, que não se cruza.

Os seis lados do hexágono são segmentos de reta, unidos em sequência pelos vértices que delimitam uma região interna.

O hexágono aparece em muitas formações na natureza, como em colmeias, cristais de gelo ou mesmo na química orgânica em estruturas de carbonos e outros átomos.

Na arquitetura e engenharia os hexágonos são utilizados como elementos estruturais, decorativos, nos parafusos e chaves, para pavimentar vias e outras utilidades.

A palavra hexágono tem origem na língua grega, em que héx se refere ao número seis e, gonía, se refere a ângulo. Portanto, uma figura com seis ângulos.

Elementos dos Hexágonos

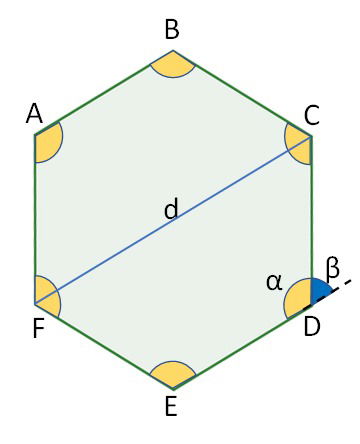
A, B, C, D, E e F são os vértices do hexágono.
Os segmentos são os lados do hexágono.
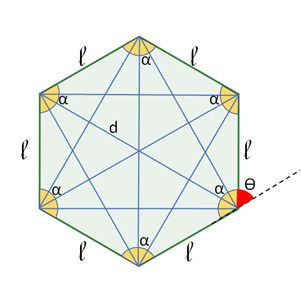
são os ângulos internos.
são os ângulos externos.
d são as diagonais.

Tipos de Hexágonos

Os hexágonos estão classificados em regulares e irregulares, convexos e não convexos, conforme as medidas de seus lados e ângulos.

Hexágonos Irregulares

Os hexágonos irregulares possuem lados e ângulos com medidas diferentes. Eles se dividem em dois grupos: os convexos e os não convexos.

Irregulares Convexos

Nos hexágonos convexos as diagonais possuem todos seus pontos na área do polígono e nenhum ângulo é maior que 180°.

Irregulares Não Convexos

Nos hexágonos não convexos, há diagonais que possuem pontos fora da área do polígono e, possuem ângulos maiores que 180°.

Hexágonos regulares

Os hexágonos regulares possuem os seis lados e ângulos de mesma medida, por isso são equiláteros e equiângulos.

Todos os hexágonos regulares são convexos, pois nenhuma diagonal passa por fora do polígono.

Um hexágono regular é uma composição de seis triângulos equiláteros.

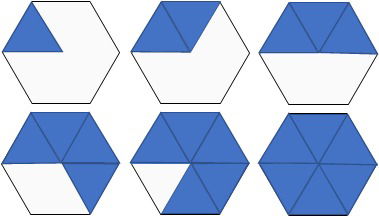
Triângulos equiláteros são os que possuem os três lados e ângulos com a mesma medida.

Área do hexágono regular

A área do hexágono é calculada pela fórmula:

Sendo L a medida do lado do hexágono, a área depende apenas de L.

Leia mais em área do hexágono.

Perímetro do hexágono regular

O perímetro do hexágono é a medida do lado multiplicada por seis.

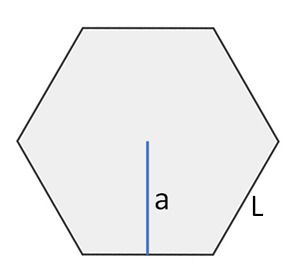
Apótema do hexágono

O Apótema do hexágono é um segmento de reta que liga o ponto médio de um lado até o ponto central do hexágono.

O apótema do hexágono regular é calculado por:

Ângulos internos dos hexágonos regulares

A medida dos ângulos internos de um hexágono regular é 120°.

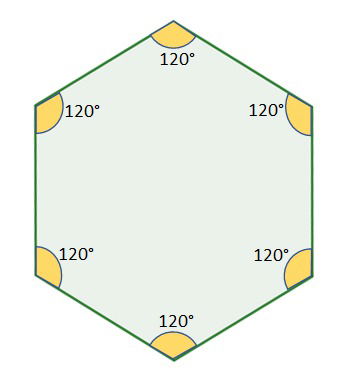
A soma dos seus ângulos internos é 720°.

120° x 6 = 720°

Ângulos externos dos hexágonos regulares

A medida dos ângulos externos de um hexágono regular é 60°.

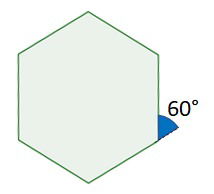
A fórmula da medida dos ângulos externos de um polígono regular é:

Onde é a medida dos ângulos externos e n é o número de lados.

Sendo n=6 nos hexágonos, temos:

Outro modo de conhecer a medida dos ângulos externos é através do par de ângulos interno e externo, pois somam 180°, sendo suplementares.

Como o ângulo interno é de 120°, basta fazer a subtração para determinar quantos graus faltam para 180°.

180° - 120° = 60°

Número de diagonais

O hexágono possui 9 diagonais.

Há duas maneiras de determinar o número de diagonais:

1ª maneira - contando.

2ª maneira - através da fórmula para diagonais de um polígono.

Em que n é o número de lados do polígono. Sendo n=6 no hexágono, temos:

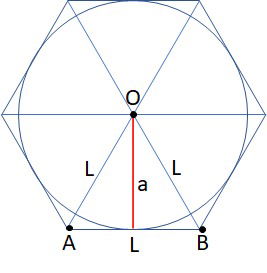
Hexágono inscrito em uma circunferência

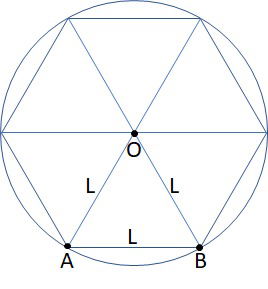
Um hexágono inscrito em uma circunferência está dentro da circunferência e, seus vértices estão sobre a circunferência.
Como o triângulo AOB da figura é equilátero, as medidas do raio da circunferência e do lado do hexágono, são iguais.

Hexágono circunscrito a uma circunferência

Um hexágono está circunscrito a uma circunferência quando a circunferência está dentro do hexágono.

A circunferência tangencia os lados do hexágono.

O raio da circunferência é igual ao apótema do hexágono. Substituindo, temos:

Então

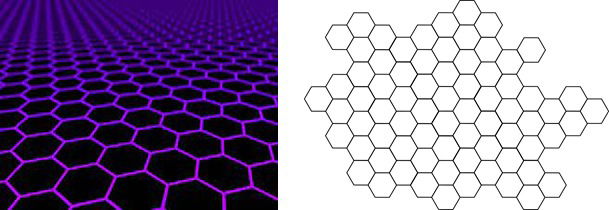
Ladrilhamento

O ladrilhamento ou tesselação é a prática de cobrir uma superfície com formas geométricas.

Os hexágonos regulares estão entre os poucos polígonos que preenchem totalmente uma superfície.

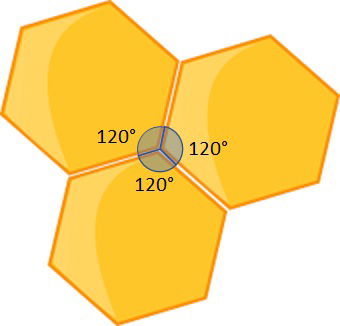
Para que um polígono regular possa ladrilhar, ou seja, preencher uma superfície sem deixar falhas, a seguinte condição geométrica deve ser satisfeita:

Os ângulos internos de um hexágono regular, medem 120°. No ladrilhamento de hexágonos, percebemos que três hexágonos se encontram em um vértice. Desse modo, temos:

120° + 120° + 120° = 360°

Exercício 1

(Enem 2021) Um estudante, morador da cidade de Contagem, ouviu dizer que nessa cidade existem ruas que formam um hexágono regular. Ao pesquisar em um sítio de mapas, verificou que o fato é verídico, como mostra a figura.

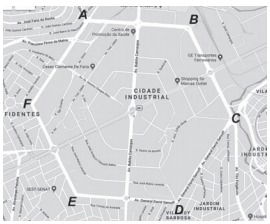
Disponível em: www.google.com. Acesso em: 7 dez. 2017 (adaptado).
Ele observou que o mapa apresentado na tela do computador estava na escala 1 : 20 000. Nesse instante, mediu o comprimento de um dos segmentos que formam os lados desse hexágono, encontrando 5 cm.
Se esse estudante resolver dar uma volta completa pelas ruas que formam esse hexágono, ele percorrerá, em quilômetro,

a) 1.
b) 4.
c) 6.
d) 20.
e) 24.

Exercício 2

(EEAR 2013) Sejam um hexágono regular e um triângulo equilátero, ambos de lado l . A razão entre os apótemas do hexágono e do triângulo é

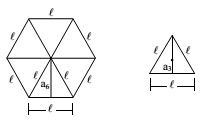
a) 4.
b) 3.
c) 2.
d) 1.

Exercício 3

(CBM-PR 2010) Considere uma placa de trânsito na forma de um hexágono regular com lados de l centímetros. Sabe-se que um hexágono regular de lados l é formado por seis triângulos equiláteros de lados l . Como a leitura desta sinalização (placa) depende da área A da placa, temos que A, em função do comprimento l, é dada por:

a)

b)

c)

d)

e)

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.