Inequação

Rafael C. Asth

Professor de Matemática e Física

Inequação é uma sentença matemática que apresenta pelo menos um valor desconhecido (incógnita) e representa uma desigualdade.

Nas inequações usamos os símbolos:

• > maior que
• < menor que
• ≥ maior que ou igual
• ≤ menor que ou igual

Exemplos

a) 3x - 5 > 62
b) 10 + 2x ≤ 20

Inequação do Primeiro Grau

Uma inequação é do 1º grau quando o maior expoente da incógnita é igual a 1. Podem assumir as seguintes formas:

• ax + b >0
• ax + b < 0
• ax + b ≥ 0
• ax + b ≤ 0

Sendo a e b números reais e a ≠ 0

Resolução de uma inequação do primeiro grau.

Para resolver uma inequação desse tipo, podemos fazer da mesma forma que fazemos nas equações.

Contudo, devemos ter cuidado quando a incógnita ficar negativa.

Nesse caso, devemos multiplicar por (-1) e inverter o símbolo da desigualdade.

Exemplos

a) Resolva a inequação 3x + 19 < 40

Para resolver a inequação devemos isolar o x, passando o 19 e o 3 para o outro lado da desigualdade.

Lembrando que ao mudar de lado devemos trocar a operação. Assim, o 19 que estava somando, passará diminuindo e o 3 que estava multiplicando passará dividindo.

3x < 40 -19
x < 21/3
x < 7

b) Como resolver a inequação 15 - 7x ≥ 2x - 30?

Quando há termos algébricos (x) dos dois lados da desigualdade, devemos juntá-los no mesmo lado.
Ao fazer isso, os números que mudam de lado tem o sinal alterado.

15 - 7x ≥ 2x - 30
- 7x - 2 x ≥ - 30 -15
- 9x ≥ - 45

Agora, vamos multiplicar toda a inequação por (-1). Para tanto, trocamos o sinal de todos os termos:

9x ≤ 45 (observe que invertemos o símbolo ≥ para ≤)
x ≤ 45/9
x ≤ 5

Portanto, a solução dessa inequação é x ≤ 5.

Resolução usando o gráfico da inequação

Outra forma de resolver uma inequação é fazer um gráfico no plano cartesiano.

No gráfico, fazemos o estudo do sinal da inequação identificando que valores de x transformam a desigualdade em uma sentença verdadeira.

Para resolver uma inequação usando esse método devemos seguir os passos:

1º) Colocar todos os termos da inequação em um mesmo lado.
2º) Substituir o sinal da desigualdade pelo da igualdade.
3º) Resolver a equação, ou seja encontrar sua raiz.
4º) Fazer o estudo do sinal da equação, identificando os valores de x que representam a solução da inequação.

Exemplo

Resolva a inequação 3x + 19 < 40.

Primeiro, vamos escrever a inequação com todos os termos de um lado da desigualdade:

3x + 19 - 40 < 0
3x - 21 < 0

Essa expressão indica que a solução da inequação são os valores de x que tornam a inequação negativa (< 0)

Encontrar a raiz da equação 3x - 21 = 0

x = 21/3
x = 7 (raiz da equação)

Representar no plano cartesiano os pares de pontos encontrados ao substituir valores no x na equação. O gráfico deste tipo de equação é uma reta.

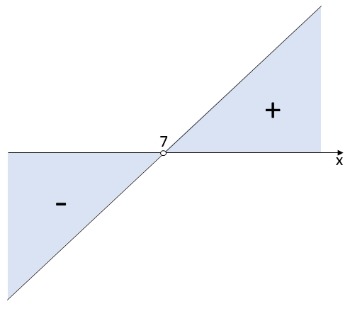
Identificamos que os valores < 0 (valores negativos) são os valores de x < 7. O valor encontrado coincide com o valor que encontramos ao resolver diretamente (exemplo a, anterior).

Inequação do Segundo Grau

Uma inequação é do 2º grau quando o maior expoente da incógnita é igual a 2. Podem assumir as seguintes formas:

• ax² + bx + c > 0
• ax² + bx + c < 0
• ax² + bx + c ≥ 0
• ax² + bx + c ≤ 0

Sendo a, b e c números reais e a ≠ 0

Podemos resolver esse tipo de inequação usando o gráfico que representa a equação do 2º grau para fazer o estudo do sinal, da mesma forma que fizemos no da inequação do 1º grau.

Lembrando que, nesse caso, o gráfico será uma parábola.

Exemplo

Resolver a inequação x² - x - 6 < 0?

Para resolver uma inequação do segundo grau é preciso encontrar valores cuja expressão do lado esquerdo do sinal < dê uma solução menor do que 0 (valores negativos).

Primeiro, identifique os coeficientes:

a = 1
b = - 1
c = - 6

Utilizamos a fórmula de Bhaskara (Δ = b² - 4ac) e substituímos pelos valores dos coeficientes:

Δ = (- 1)² - 4 . 1 . (- 6)
Δ = 1 + 24
Δ = 25

Continuando na fórmula de Bhaskara, substituímos novamente pelos valores dos nossos coeficientes:

x = (1 ± √25) / 2
x = (1 ± 5) / 2

x₁ = (1 + 5)/ 2
x₁ = 6 / 2
x₁ = 3

x₂ = (1 - 5) / 2
x₁ = - 4 / 2
x₁ = - 2

As raízes da equação são -2 e 3. Como o coeficiente a da equação do 2º grau é positivo, seu gráfico terá a concavidade voltada para cima.

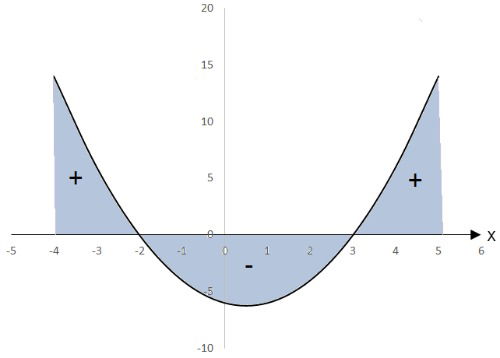
Pelo gráfico, observamos que os valores que satisfazem a inequação são: - 2 < x < 3

Podemos indicar a solução usando a seguinte notação:

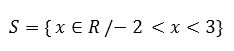
Um número x que pertence ao conjunto dos números Reais, tal que, x seja maior que -2 e menor que 3.

Leia também:

• Equação do Primeiro Grau
• Equação do Segundo Grau
• Sistemas de Equações

Exercícios

Questão 1

(FUVEST 2008). Por recomendação médica, uma pessoa deve fazer, durante um curto período, dieta alimentar que lhe garanta um mínimo diário de 7 miligramas de vitamina A e 60 microgramas de vitamina D, alimentando-se exclusivamente de um iogurte especial e de uma mistura de cereais, acomodada em pacotes.

Cada litro do iogurte fornece 1 miligrama de vitamina A e 20 microgramas de vitamina D. Cada pacote de cereais fornece 3 miligramas de vitamina A e 15 microgramas de vitamina D.

Consumindo x litros de iogurte e y pacotes de cereais diariamente, a pessoa terá certeza de estar cumprindo a dieta se:

a) x + 3y ≥ 7 e 20x + 15y ≥ 60
b) x + 3y ≤ 7 e 20x + 15y ≤ 60
c) x + 20y ≥ 7 e 3x + 15y ≥ 60
d) x + 20y ≤ 7 e 3x + 15y ≤ 60
e) x + 15y ≥ 7 e 3x + 20y ≥ 60

Questão 2

(UFC 2002). Uma cidade é servida por duas empresas de telefonia. A empresa X cobra, por mês, uma assinatura de R$35,00 mais R$0,50 por minuto utilizado. A empresa Y cobra, por mês, uma assinatura de R$26,00 mais R$0,65 por minuto utilizado. A partir de quantos minutos de utilização o plano da empresa X passa a ser mais vantajoso para os clientes do que o plano da empresa Y?

Pratique mais:

• Exercícios de inequações
• Exercícios de equação biquadrada

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.