Lei dos Cossenos
A Lei dos Cossenos é utilizada para calcular a medida de um lado ou de um ângulo desconhecido de um triângulo qualquer, conhecendo suas outras medidas.
A lei dos cossenos pode ser aplicada em qualquer triângulo. Seja ele acutângulo (ângulos internos menores que 90º), obtusângulo (com um ângulo interno maior que 90º), ou retângulo (com um ângulo interno igual a 90º).
O teorema dos cossenos estabelece que:
"Em qualquer triângulo, o quadrado de um dos lados corresponde à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles."
Fórmula da Lei dos Cossenos
Assim, pela lei dos cossenos temos as seguintes relações entre os lados e os ângulos de um triângulo:
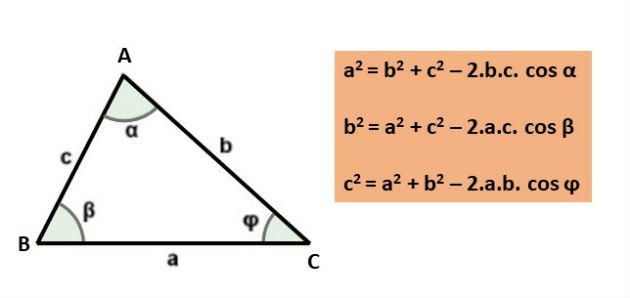
Exemplo 1: Dois lados de um triângulo medem 20 cm e 12 cm e formam entre si um ângulo de 120º. Calcule a medida do terceiro lado.
Resolução:
Para calcular a medida do terceiro lado utilizaremos a lei dos cossenos. Para isso, vamos considerar:
b = 20 cm
c = 12 cm
cos α = cos 120º = - 0,5 (valor encontrado em tabelas trigonométricas).
Substituindo esses valores na fórmula:
a2 = 202 + 122 - 2 . 20 . 12 . (- 0,5)
a2 = 400 + 144 + 240
a2 = 784
a = √784
a = 28 cm
Conclusão:
O terceiro lado mede 28 cm.
Exemplo 2: Determine a medida do lado AC e a medida do ângulo com vértice em A da figura a seguir:
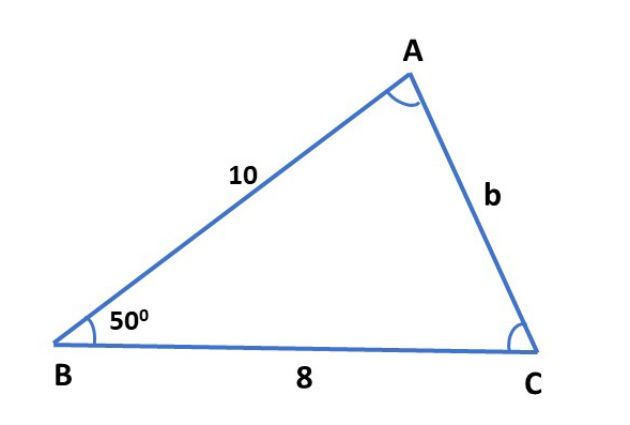
Resolução:
Primeiramente, vamos determinar o AC = b:
b2 = 82 + 102 – 2 . 8 . 10 . cos 50º
b2 = 164 – 160 . cos 50º
b2 = 164 – 160 . 0,64279
b ≈ 7,82
Agora, vamos determinar a medida do ângulo pela lei dos cossenos:
82 = 102 + 7,822 – 2 . 10 . 7,82 . cos Â
64 = 161,1524 – 156,4 . cos Â
cos  = 0,62
 = 52º
Obs: Para encontrar os valores dos ângulos do cosseno utilizamos a Tabela Trigonométrica. Nela, temos os valores dos ângulos de 1º a 90º para cada função trigonométrica (seno, cosseno e tangente).
Lei dos cossenos no triângulo retângulo
Vamos aplicar a lei dos cossenos para o lado oposto ao ângulo de 90º, conforme indicado abaixo:
a2 = b2 + c2 - 2 . b . c . cos 90º
Como cos 90º = 0, a expressão acima fica:
a2 = b2 + c2
Que é igual à expressão do Teorema de Pitágoras. Assim, podemos dizer que este teorema é um caso particular da lei dos cossenos.
A lei dos cossenos é adequada para problemas em que conhecemos dois lados e o ângulo entre eles e descobrimos o terceiro lado.
Podemos ainda a utilizar quando conhecemos os três lados do triângulo e pretendemos conhecer um dos seus ângulos.
Para situações em que conhecemos dois ângulos e apenas um lado e determinamos outro lado, torna-se mais conveniente utilizar a Lei dos Senos.
Exercícios sobre a lei dos cossenos
Exercício 1
(UFSCar) Se os lados de um triângulo medem x, x + 1 e x + 2, então, para qualquer x real e maior que 1, o cosseno do maior ângulo interno desse triângulo é igual a:
a) x / x + 1
b) x / x + 2
c) x + 1 / x + 2
d) x – 2 / 3x
e) x – 3 / 2x
Exercício 2
(UFRS) No triângulo representado na figura abaixo, AB e AC têm a mesma medida, e a altura relativa ao lado BC é igual a 2/3 da medida de BC.
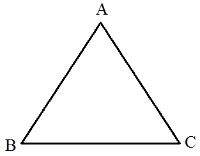
Com base nesses dados, o cosseno do ângulo CÂB é:
a) 7/25
b) 7/20
c) 4/5
d) 5/7
e) 5/6
Exercício 3
(UF-Juiz de Fora) Dois lados de um triângulo medem 8 m e 10 m e formam um ângulo de 60°. O terceiro lado desse triângulo mede:
a) 2√21 m
b) 2√31 m
c) 2√41 m
d) 2√51 m
e) 2√61 m
Leia mais sobre o tema:
Definição de Cosseno e Seno
O cosseno e o seno de um ângulo são definidos como razões trigonométricas em um triângulo retângulo. O lado oposto ao ângulo reto (90º) é chamado de hipotenusa e os outros dois lados são chamados de catetos, conforme representado na figura abaixo:
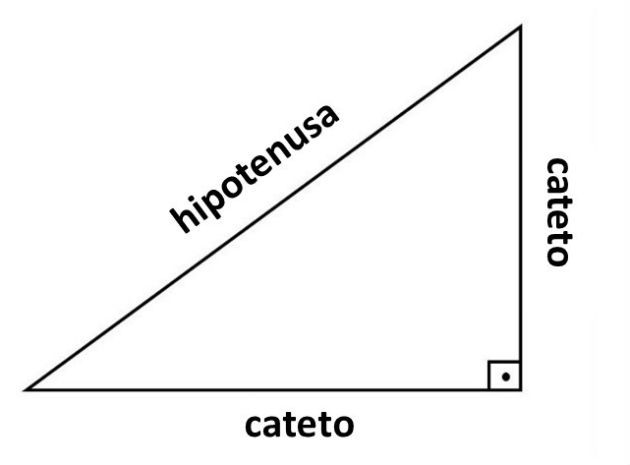
O cosseno é então definido como a razão entre a medida do cateto adjacente e da hipotenusa:
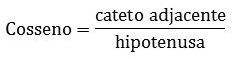
Já o seno, é a razão entre a medida do cateto oposto e a hipotenusa.
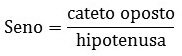
GOUVEIA, Rosimar. Lei dos Cossenos. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/lei-dos-cossenos/. Acesso em:



