O que é e como calcular a Proporção Áurea
A proporção áurea, também conhecida como “razão áurea” ou “número de ouro”, é uma constante matemática representada pela letra grega ϕ (phi), com valor de aproximadamente 1,6180339887…
Essa proporção aparece em muitos contextos, desde a arte e arquitetura até a natureza, onde é frequentemente associada à beleza e harmonia.
A proporção áurea foi estudada pelos matemáticos da Grécia Antiga, especialmente por Euclides em seu trabalho “Os Elementos”. No entanto, o termo “proporção áurea” foi popularizado apenas durante o Renascimento, quando artistas e arquitetos passaram a usá-la como uma ferramenta para alcançar uma estética harmoniosa.
Número de Ouro ϕ (phi): 1,6180339887…
O número de Ouro é um valor numérico irracional, possuindo infinitas casas decimais não periódicas. Após a parte inteira, o 1, seguem-se suas casas decimais sem repetição periódica.
Seu valor é aproximadamente obtido por meio de uma proporção, uma igualdade entre razões. É preciso que as partes destas razões obedeçam a uma proporção exata.
Para chegar ao número de Ouro, considere um segmento de reta separado em duas partes desiguais (um maior que o outro).
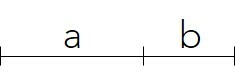
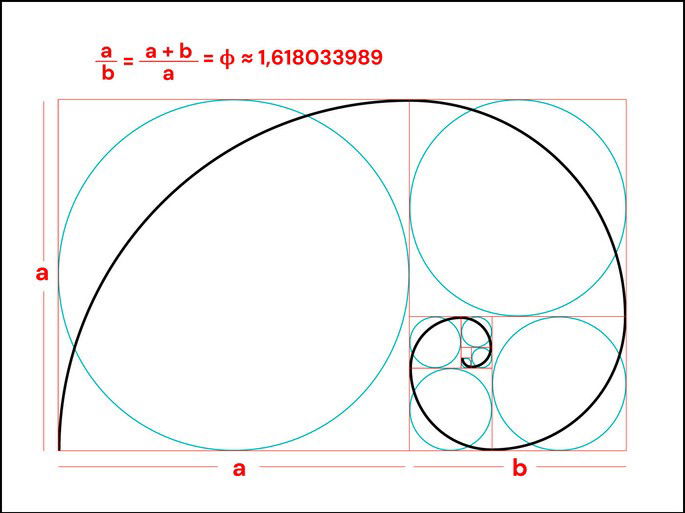
A razão entre o comprimento total (a + b) e a parte maior (a) é igual à razão entre a parte maior (a) e a menor (b).
Matematicamente, isso pode ser expresso como:
O nome proporção se refere ao processo matemático para medir os segmentos a e b que respeitem a igualdade.
Como calcular a Proporção Áurea (passo a passo)
Vamos aprender como calcular a Proporção Áurea usando um exemplo simples: um seguimento de reta com 100 cm será dividido em duas partes, conforme a proporção.
Passo 1: estabelecer a relação entre as partes a e b, sendo a a maior.
Temos que a + b = 100, logo, b = 100 - a.
Se 100 cm é a medida total e a é a maior, (100 - a) é a medida do segmento menor, o b.
Passo 2: substituir estes valores na proporção.
Passo 3: calcular a medida do seguimento maior a.
Aplicamos a propriedade fundamental das proporções multiplicando “cruzado”.
Devemos resolver a equação do 2º grau, com a = 1, b = 100 e c = -10 000.
Perceba que aproximamos o valor da raiz quadrada de 50 000.
Para o cálculo de a2, adotamos o valor negativo da raiz.
No entanto, como estamos tratando de uma medida de comprimento, não faz sentido considerar o valor negativo.
Passo 4: obter o valor do segmento menor, b.
Como a + b = 100 e, b = 100 - a, temos:
Conclusão
Nosso segmento de reta com 100 cm foi dividido em duas partes conforme a proporção áurea, sendo:
a = 61,8 cm e b = 38,2 cm
Como calcular o Número de Ouro
O cálculo do Número de Ouro surge da divisão entre as partes segundo a proporção: . É preciso frisar que o resultado será sempre um valor aproximado, pois se trata de um número irracional.
Exemplo: cálculo do Número de Ouro a partir dos segmentos a = 61,8 cm e b = 38,2 cm.
Utilizaremos os valores calculados no exemplo anterior.
O valor obtido é, aproximadamente o número ϕ (1,6180339887 ...).
Você pode se interessar pelos números irracionais e proporções.
Exemplos da Proporção Áurea na natureza
A proporção áurea aparece em vários fenômenos naturais, refletindo uma ordem e simetria que associamos muitas vezes à beleza.
- Conchas de Nautilus: A espiral encontrada na concha do Nautilus segue aproximadamente a proporção áurea, à medida que as espirais crescem de maneira constante em relação ao centro.
- Girassóis: As sementes de um girassol se organizam em espirais que seguem a proporção áurea, permitindo um arranjo compacto e eficiente.
- Galáxias Espirais: A forma das galáxias espirais, como a Via Láctea, também segue uma espiral logarítmica relacionada à proporção áurea.

A Proporção Áurea na Arte e Arquitetura
A proporção áurea tem sido usada como uma ferramenta de design para criar obras de arte e arquitetura consideradas esteticamente agradáveis.
- O Parthenon na Grécia: A fachada do Parthenon é projetada conforme a proporção áurea, refletindo a harmonia e equilíbrio desejados pelos gregos antigos.
- A Mona Lisa de Leonardo da Vinci: A composição da Mona Lisa também utiliza a proporção áurea para distribuir os elementos da pintura de maneira equilibrada e harmoniosa.

A Relação entre a Proporção Áurea e a Sequência de Fibonacci
A Proporção Áurea e a sequência Fibonacci estão diretamente ligadas.
À medida que avançamos na sequência de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, 34...), a razão entre números consecutivos da sequência se aproxima do valor da Proporção Áurea (aproximadamente 1,618).
Por exemplo, ao dividir 21 por 13, ou 34 por 21, o quociente se aproxima cada vez mais de 1,618.
| Elemento n | Elemento n - 1 | Divisão |
|---|---|---|
| 2 | 1 | 2 |
| 3 | 2 | 1,5 |
| 5 | 3 | 1,666 |
| 8 | 5 | 1,6 |
| 13 | 8 | 1,625 |
| 21 | 13 | 1,615 |
| 34 | 21 | 1,619 |
| 55 | 34 | 1,617 |
| 89 | 55 | 1,618 |
Essa relação revela que a sequência de Fibonacci é uma representação numérica da Proporção Áurea, mostrando que padrões numéricos e proporções estão frequentemente presentes na natureza e na arte.
Essa conexão explica por que tanto a sequência quanto a Proporção Áurea aparecem em fenômenos naturais, como a disposição das pétalas de uma flor ou a formação de conchas.
Aprenda mais sobre a Sequência de Fibonacci.
ASTH, Rafael. O que é e como calcular a Proporção Áurea. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/o-que-e-e-como-calcular-a-proporcao-aurea/. Acesso em:


