Perímetro do Retângulo: como calcular e exercícios
O perímetro do retângulo é a soma das medidas de todos os lados dessa figura geométrica plana.
Podemos definir perímetro como a medida que delimita uma figura plana fechada. Como o retângulo possui quatro lados, calcular seu perímetro é somar as medidas de seus quatro lados.
Fórmula do perímetro do retângulo
Como o retângulo possui dois pares de lados paralelos, a fórmula para o perímetro é:
ou
Colocando o 2 em evidência, também podemos reescrever como:
Sendo,
P o perímetro,
b a base,
h a altura.
As três fórmulas acima são, na verdade, a mesma, apenas escritas de formas diferentes. Você pode escolher a que melhor se adapte às suas necessidades.
Características do Retângulo
Lembre-se que o retângulo é uma figura plana composta de 4 lados, e por isso, é considerado um quadrilátero.
Dois lados do retângulo são menores e indicam geralmente a altura (h) ou a largura. E, dois lados são maiores e indicam a base (b) ou o comprimento da figura.
No entanto, há retângulos onde a altura é maior que a base.
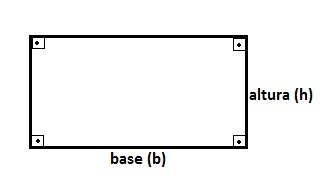
Em outras palavras, dois lados dos retângulos são paralelos verticalmente e dois lados paralelos horizontalmente.
Em relação aos ângulos, ele é formado por 4 ângulos retos (de 90° cada) sendo que a soma de seus ângulos internos totaliza 360°.
Área do Retângulo
Muito comum haver confusão entre os conceitos de área e perímetro. No entanto, eles apresentam diferenças:
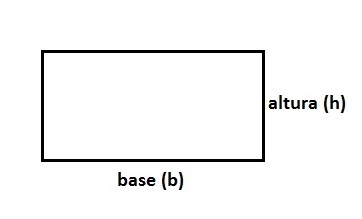
Área: valor da superfície retangular, sendo calculado pela multiplicação entre a altura (h) e a base (b) do retângulo. É expresso pela fórmula:
.
Leia também os artigos:
Obs: Note que para encontrar o perímetro de outras figuras planas (quadrado, trapézio, triângulo) também somamos os lados da figura.
Ou seja, num triângulo, o perímetro será a soma dos três lados, no quadrado, a soma dos quatro lados, etc.
Diagonal do Retângulo
A diagonal do retângulo corresponde a reta que divide a figura em dois. Ou seja, quando temos uma diagonal do retângulo, ele apresenta dois triângulos retângulos.
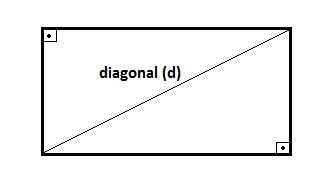
Os triângulos retângulos recebem esse nome pois um de seus lados forma um ângulo reto (90°).
A diagonal corresponde à hipotenusa do triângulo retângulo. Feita essa observação, para encontrar a diagonal utiliza-se a fórmula do Teorema de Pitágoras:
Assim, a fórmula para calcular a diagonal do retângulo é:
Exercícios sobre perímetro do retângulo
Para fixar os conceitos sobre o perímetro, vejamos abaixo dois exercícios comentados.
Exercício 1
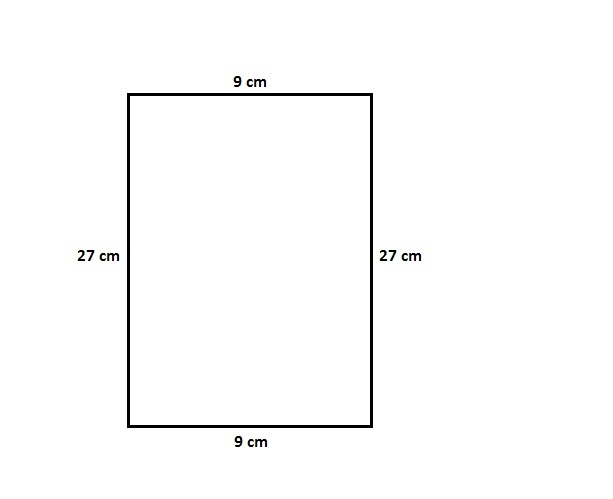
Calcule os perímetros dos retângulos abaixo:

Exercício 2
Calcule a área de um retângulo cujo perímetro mede 72 cm e a altura mede o triplo da base.
Que tal saber também sobre o Perímetro do Quadrado?
Veja também:
ASTH, Rafael. Perímetro do Retângulo: como calcular e exercícios. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/perimetro-do-retangulo/. Acesso em: