Perímetros de Figuras Planas: o que é e aprenda a calcular

Os perímetros de figuras planas indicam o valor da medida do contorno da figura. Ou seja, o conceito de perímetro corresponde à soma de todos os lados de uma figura geométrica plana, incluindo curvas.

Ele representa a medida total ao redor da borda dessa figura. Em termos práticos, o perímetro é usado, por exemplo, para calcular o comprimento de cercas, muros ou qualquer outra estrutura que envolva contornar uma área.

Perímetro do Triângulo

O triângulo é uma figura plana formada por três lados e ângulos internos. Para calcular seu perímetro, basta somar as medidas dos três lados.

Onde: a, b e c são as medidas dos lados do triângulo.

Conforme a medida dos lados eles podem ser:

• Triângulo Equilátero: lados e ângulos internos iguais (60°);
• Triângulo Isósceles: dois lados e dois ângulos internos congruentes;
• Triângulo Escaleno: todos os lados e ângulos internos são diferentes.

E, segundo a medida dos ângulos, eles são classificados em:

• Triângulo Retângulo: um ângulo interno de 90°;
• Triângulo Obtusângulo: dois ângulos agudos internos (menor que 90°), e um ângulo obtuso interno (maior que 90°);
• Triângulo Acutângulo: três ângulos internos menores que 90°.

Leia mais:

• Área do Triângulo
• Perímetro do Triângulo
• Classificação dos Triângulos

Perímetro do Quadrado

O quadrado é uma figura plana formada por quatro lados congruentes (mesma medida). Possui quatro ângulos internos de 90° (ângulos retos).

Para calcular o perímetro do quadrado, basta multiplicar por quatro a medida do lado.

Onde L é a medida do lado.

Leia mais:

• Área do Quadrado
• Perímetro do Quadrado

Perímetro do Retângulo

É uma figura plana formada por quatro lados, donde dois deles são menores. Também possui quatro ângulos internos de 90°.

Para calcular o perímetro do retângulo, fazemos:

Onde: c é a medida do comprimento e l a largura.

Leia mais:

• Retângulo
• Área do Retângulo
• Perímetro do Retângulo

Perímetro do Círculo

O círculo é uma figura plana que também é chamada de disco. Seu perímetro é calculado multiplicando a medida do raio e do número por dois.

Leia mais:

• Área do Círculo
• Perímetro do Círculo

Perímetro do Trapézio

Os trapézios são figuras planas formadas por quatro lados. Apresentam dois lados (bases) paralelos, sendo um menor e outro maior.

Para calcular o perímetro do trapézio, deve-se somar as medidas dos lados.

Onde:

• B e b são as medidas das bases (maior e menor);
• a e c são as medidas dos outros lados.

Segundo a medida dos lados e ângulos eles são classificados em:

• Trapézio Retângulo: possui dois ângulos de 90º;
• Trapézio Isósceles ou Simétrico: os lados não paralelos possuem a mesma medida;
• Trapézio Escaleno: todos os lados possuem medidas diferentes.

Leia mais:

• Trapézio
• Área do Trapézio

Perímetro do Losango

Figura plana formada por quatro lados iguais. Possui lados e ângulos opostos congruentes e paralelos.

O perímetro do losango é calculado multiplicando por quatro a medida do lado (L).

Saiba sobre a Área do Losango.

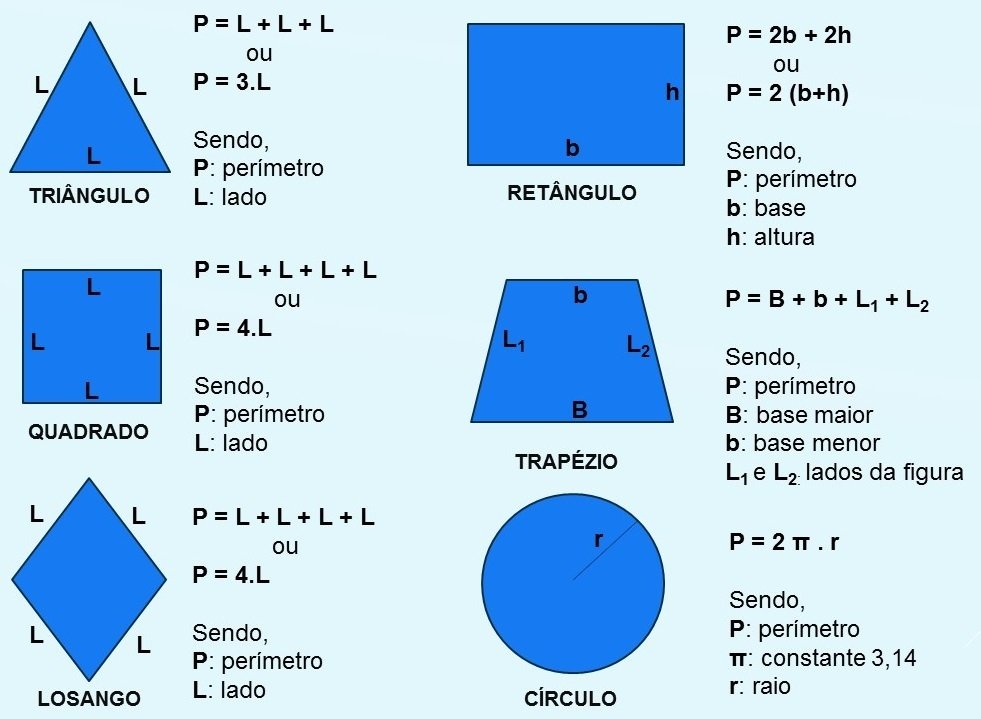
Resumo de Fórmulas dos Perímetros

Para calcular cada uma das figuras planas apresentadas acima, utilizam-se as seguintes fórmulas:

Perímetro e Área de Figuras Planas

É comum haver confusão entre o conceito de área e perímetro. No entanto, a área é a medida da superfície de uma figura plana. Já o perímetro é a medida do seu contorno.

As unidades de medida utilizadas para perímetro são as de comprimento, por exemplo: metro (m), centímetro (cm) ou quilômetro (km). Já as unidades de área são quadradas, por exemplo: m², cm² ou km².

Saiba mais sobre o tema:

• Área e Perímetro
• Áreas de Figuras Planas

Leia também sobre Quadriláteros.

Exercícios sobre cálculo do perímetro

Exercício 1

Um triângulo possui lados com medidas de 6 cm, 8 cm e 10 cm. Determine seu perímetro.

Exercício 2

Um retângulo tem 12 cm de comprimento e 5 cm de largura. Qual é o perímetro desse retângulo?

Exercício 3

Considere um círculo com raio de 7 cm. Use π = 3,14. Qual é o perímetro (circunferência) desse círculo?

Exercício 4

(Enem-2011) Em uma certa cidade, os moradores de um bairro carente de espaços de lazer reivindicam à prefeitura municipal a construção de uma praça. A prefeitura concorda com a solicitação e afirma que irá construí-la em formato retangular devido às características técnicas do terreno. Restrições de natureza orçamentária impõem que sejam gastos, no máximo, 180 m de tela para cercar a praça. A prefeitura apresenta aos moradores desse bairro as medidas dos terrenos disponíveis para a construção da praça:

Terreno 1: 55 m por 45 m
Terreno 2: 55 m por 55 m
Terreno 3: 60 m por 30 m
Terreno 4: 70 m por 20 m
Terreno 5: 95 m por 85 m

Para optar pelo terreno de maior área, que atenda às restrições impostas pela prefeitura, os moradores deverão escolher o terreno.

a) 1
b) 2
c) 3
d) 4
e) 5

Confira mais questões, com resolução comentada, em Exercícios sobre Área e Perímetro.