Poliedro: o que é, classificação, exercícios

Revisão por Rafael C. Asth

Professor de Matemática e Física

Os poliedros são sólidos geométricos, formas com três dimensões, limitados por um número finito de polígonos planos. Esses polígonos formam as faces do poliedro.

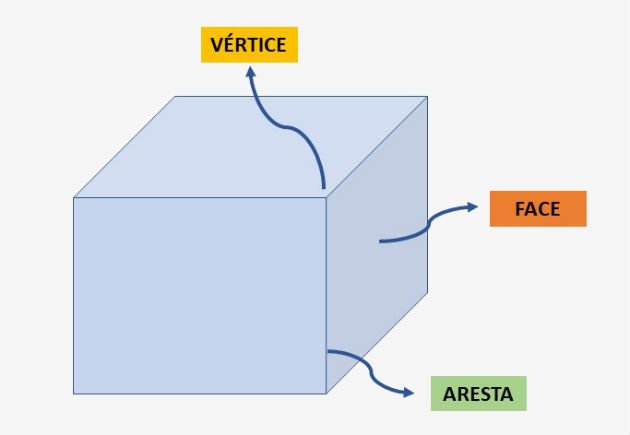
A intersecção de duas faces é chamada de aresta e o ponto comum de três ou mais arestas é chamado de vértice, conforme indicado na imagem abaixo.

Para ser considerado um poliedro, a forma não deve possuir faces curvas.

Os poliedros são classificados como convexos ou não convexos e podem ser regulares (com todas as faces e ângulos iguais) ou irregulares.

Poliedro convexo e não convexo

Os poliedros podem ser classificados como convexos ou não convexos. Um poliedro é considerado convexo se qualquer segmento de reta que conecta dois pontos em seu interior estiver completamente contido dentro dele.

Outra maneira de identificar um poliedro convexo é observar que qualquer reta que não esteja contida em nenhuma de suas faces nem seja paralela a elas intersecta os planos das faces em, no máximo, dois pontos.

Fórmula de Euler: relação entre vértices, faces e arestas

O Teorema ou Fórmula de Euler é válido para os poliedros convexos e para alguns poliedros não-convexos. Este teorema estabelece a seguinte relação entre o número de faces, vértices e arestas:

Onde,

F: número de faces
V: número de vértices
A: número de arestas

Os poliedros onde a relação de Euler é válida são chamados de eulerianos. É importante notar que todo poliedro convexo é euleriano, porém nem todo poliedro euleriano é convexo.

Exemplo

Um poliedro convexo é formado por exatamente 4 triângulos e 1 quadrado. Quantos vértices tem esse poliedro?

Resolução

Primeiro precisamos definir a quantidade de faces e arestas. Como o poliedro possui 4 triângulos e 1 quadrado, então possui 5 faces.

Para encontrar o número de arestas podemos calcular o número total de lados e dividir o resultado por dois, visto que cada aresta é a intersecção de dois lados:

Agora que conhecemos o número de faces e arestas, podemos aplicar a relação de Euler, assim temos:

Portanto, este poliedro possui 5 vértices.

Veja mais sobre a relação de Euler.

Poliedros regulares: os sólidos de Platão

Os poliedros convexos são regulares quando suas faces são compostas por polígonos regulares e congruentes entre si. Além disso, o número de aresta em cada vértice é o mesmo.

Devemos lembrar que os polígonos regulares são aqueles que possuem todos os lados e ângulos congruentes, ou seja, com mesma medida.

Existem apenas cinco poliedros regulares convexos, designados por “Sólidos Platônicos” ou “Poliedros de Platão”. São eles: tetraedro, hexaedro (cubo), octaedro, dodecaedro, icosaedro.

• Tetraedro: sólido geométrico formado por 4 vértices, 4 faces triangulares e 6 arestas.
• Hexaedro: sólido geométrico formado por 8 vértices, 6 faces quadrangulares e 12 arestas.
• Octaedro: sólido geométrico formado por 6 vértices, 8 faces triangulares e 12 arestas.
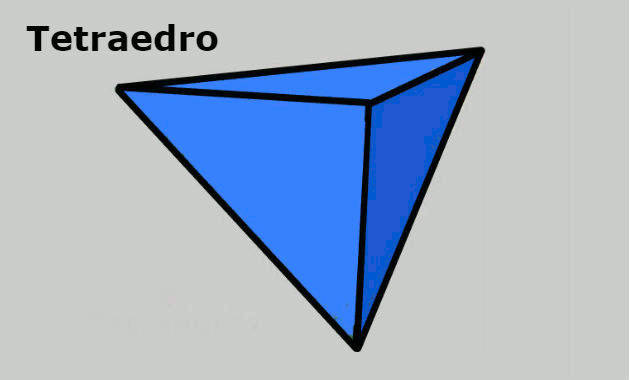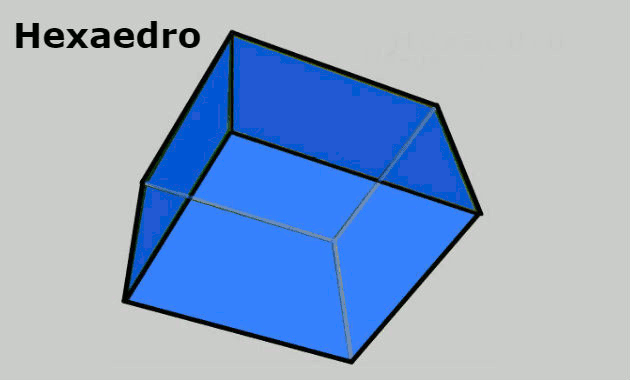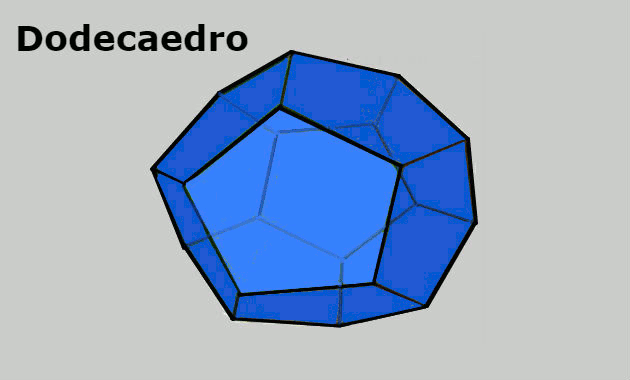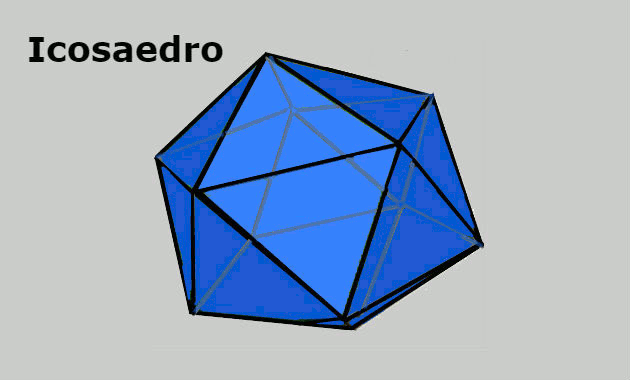
• Dodecaedro: sólido geométrico formado por 20 vértices, 12 faces pentagonais e 30 arestas.
• Icosaedro: sólido geométrico formado por 12 vértices, 20 faces triangulares e 30 arestas.

Prismas

Os prismas são sólidos geométricos que apresentam duas bases formadas por polígonos congruentes e localizados em planos paralelos. Suas faces laterais são paralelogramos ou retângulos.

Conforme a inclinação das arestas laterais em relação à base, os prismas são classificados em retos ou oblíquos.

As faces laterais dos prismas retos são retângulos, enquanto dos prismas oblíquos são paralelogramos, conforme imagem abaixo:

Pirâmide

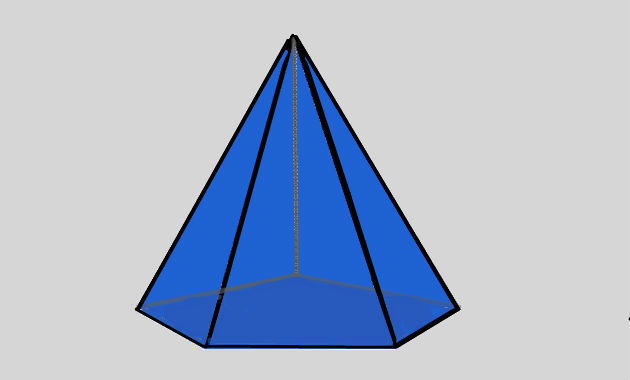
As pirâmides são sólidos geométricos formados por uma base poligonal e um vértice (vértice da pirâmide) que une todas as faces laterais triangulares.

O número de lados do polígono da base corresponde ao número de faces laterais da pirâmide.

Saiba mais sobre o tema:

• Volume da Pirâmide
• Geometria Espacial
• Formas Geométricas
• Sólidos Geométricos
• Pirâmide
• Volume do Prisma

Exercícios sobre poliedros

Exercício 1

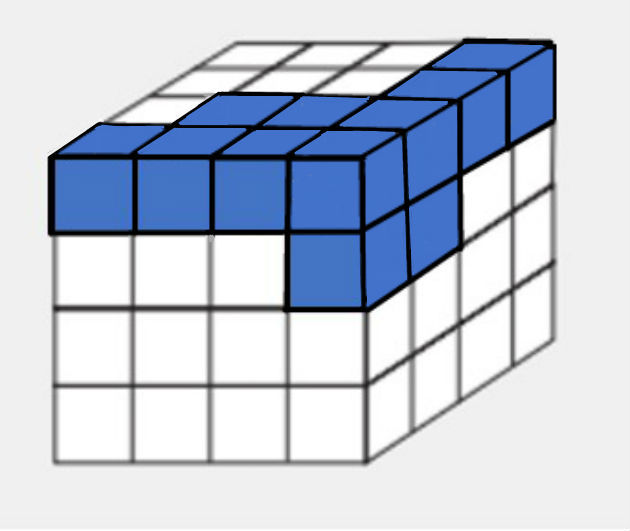
(Enem - 2018) Minecraft é um jogo virtual que pode auxiliar no desenvolvimento de conhecimentos relacionados a espaço e forma. É possível criar casas, edifícios, monumentos e até naves espaciais, tudo em escala real, através do empilhamento de cubinhos.

Um jogador deseja construir um cubo com dimensões 4 x 4 x 4. Ele já empilhou alguns dos cubinhos necessários, conforme a figura.

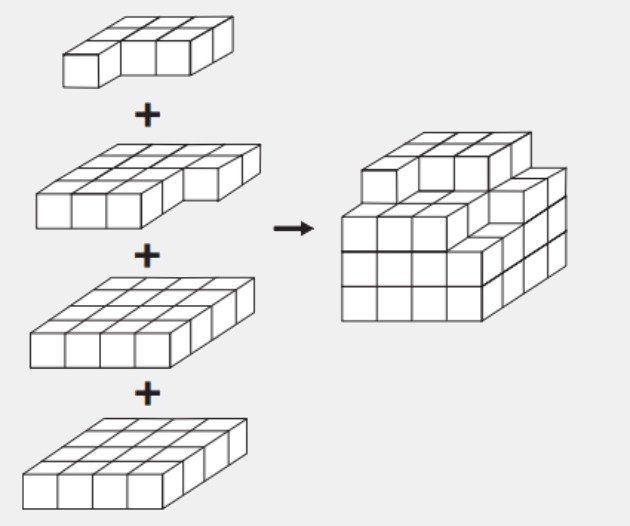
Os cubinhos que ainda faltam empilhar para finalizar a construção do cubo, juntos, formam uma peça única, capaz de completar a tarefa.

O formato da peça capaz de completar o cubo 4 x 4 x 4 é

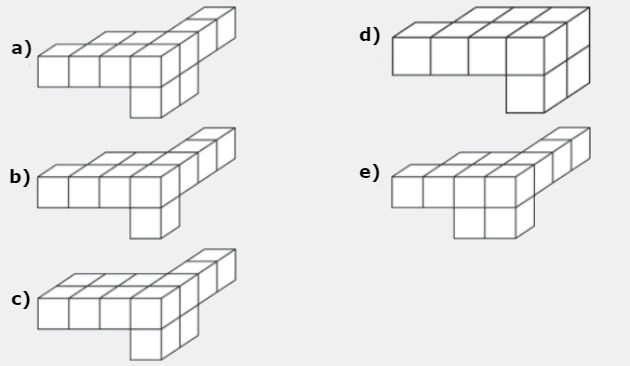
Exercício 2

(Enem - 2017) Uma rede hoteleira dispõe de cabanas simples na ilha de Gotland, na Suécia, conforme Figura 1. A estrutura de sustentação de cada uma dessas cabanas está representada na Figura 2. A ideia é permitir ao hóspede uma estada livre de tecnologia, mas conectada com a natureza.

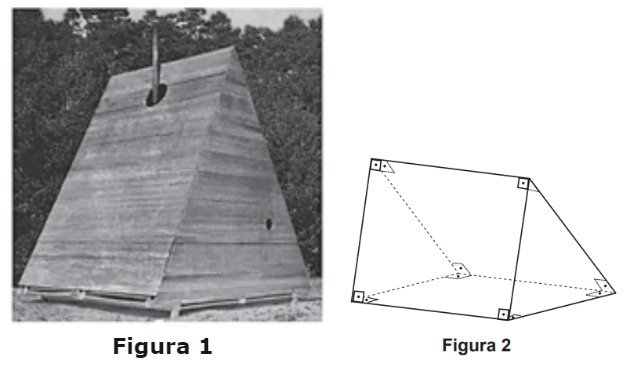
A forma geométrica da superfície cujas arestas estão representadas na Figura 2 é

a) tetraedro.
b) pirâmide retangular.
c) tronco de pirâmide retangular.
d) prisma quadrangular reto.
e) prisma triangular reto.

Curiosidade

Ao estudar os poliedros regulares, o filósofo e matemático grego Platão relacionou cada um deles com os elementos da natureza: tetraedro (fogo), hexaedro (terra), octaedro (ar), dodecaedro (universo) e icosaedro (água).

Revisão por Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Edição por Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.