Polígonos regulares: o que são, propriedades e exemplos

Rafael C. Asth

Professor de Matemática e Física

Um polígono é regular quando é convexo e possui todos os lados e ângulos de mesma medida. Por isso um polígono regular é equilátero, pois todos os lados são de mesmo comprimento, e equiângulo, visto que todos os ângulos possuem a mesma medida.

A definição de polígono é de uma figura fechada, plana, formada por segmentos de reta não alinhados e que não se cruzam. Estes segmentos são os lados do polígono que, quando regular, são de mesmo comprimento.

O encontro de dois lados é um vértice e, a área entre os lados é chamada ângulo interno, medido em grau. Nos polígonos regulares os ângulos são congruentes.

Um polígono possui o mesmo número de lados, vértices, ângulos internos (ai) e externos (ae).

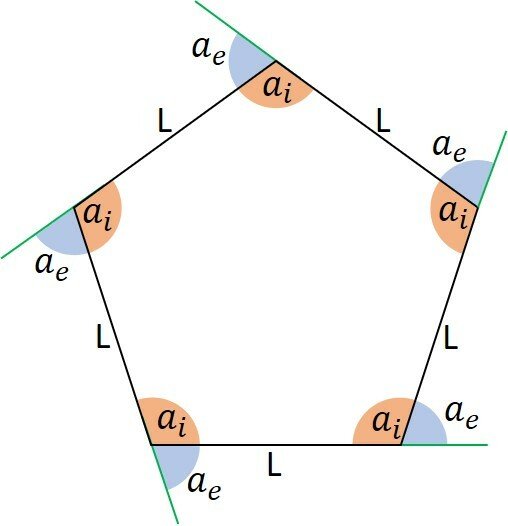
Polígono regular e seus elementos.

Os polígonos regulares são convexos, equiláteros e equiângulos, pois seus lados e ângulos são congruentes. As três condições devem ser satisfeitas.

Um polígono é convexo quando todo e qualquer segmento liga dois pontos em seu interior, sem que nenhuma parte do segmento fique fora da área do polígono.

Perímetro de polígonos regulares

O perímetro de um polígono é a soma das medidas de seus lados. Como em um polígono regular, todos os lados possuem a mesma medida, basta multiplicar a medida de um lado pelo número de lados do polígono.

$começar estilo tamanho matemático 18px reto P espaço igual a espaço reto n espaço. espaço reto L fim do estilo$

Onde,
P é o perímetro,
n é o número de lados,
L é o comprimento dos lados.

Exemplo
O perímetro do hexágono regular com lados de 7 cm é:

$P igual a n espaço. espaço L igual a 6 espaço. espaço 7 espaço igual a espaço 42 espaço c m espaço$

Ângulos internos

Um ângulo interno é a região formada entre dois lados que se encontram em um vértice. Em um polígono regular todos os ângulos internos são de mesma medida.

Da mesma forma, se o valor da soma dos ângulos é conhecida, a medida de um ângulo é o total divido pelo número de ângulos.

$reto a com reto i subscrito igual a reto S com reto i subscrito sobre reto n$

Soma dos ângulos internos de polígono

Se a medida de um ângulo interno é conhecida, é possível determinar a soma dos ângulos internos ao multiplicar seu valor pelo número de ângulos.

$reto S com reto i subscrito igual a reto a com reto i espaço subscrito fim do subscrito. espaço reto n$

Onde:
$reto S com reto i subscrito$ é a soma dos ângulos internos do polígono;
$reto a com reto i subscrito$ é a medida de um ângulo interno;
n é o número de ângulos internos.

Para determinar a soma dos ângulos internos de um polígono sem conhecer a medida de um ângulo, utilizamos a fórmula:

$começar estilo tamanho matemático 20px reto S com reto i subscrito igual a 180 espaço. espaço parêntese esquerdo reto n menos 2 parêntese direito fim do estilo$

Exemplo
A soma dos ângulos internos de um polígono regular com 6 lados e a medida de cada ângulo é:

$reto S com reto i subscrito igual a 180 espaço. espaço parêntese esquerdo reto n menos 2 parêntese direito espaço igual a espaço 180 espaço. espaço parêntese esquerdo 6 menos 2 parêntese direito espaço igual a espaço 180 espaço. espaço 4 espaço igual a espaço 720 sinal de grau$ .

A medida de cada ângulo é

$a com i subscrito igual a S com i subscrito sobre n igual a 720 sobre 6 igual a espaço 120 sinal de grau$ .

Apótema de um polígono regular

O apótema de um polígono regular é um segmento de reta que une o centro do polígono ao ponto médio de um lado, fazendo com este um ângulo de 90°.

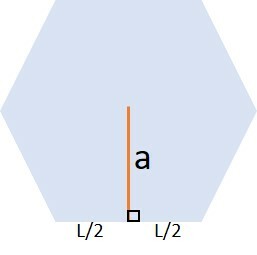
Desta forma, o apótema divide um lado em duas partes iguais, sendo uma mediatriz, pois divide o lado exatamente ao meio.

A quantidade de apótemas de um polígono é a mesma de seu número de lados. Como o polígono é regular, os apótemas possuem mesma medida.

Área de polígonos regulares

Um modo de calcular a área de qualquer polígono regular, independente de seu número de lados, é multiplicar seu semiperímetro pelo seu apótema.

O semiperímetro é a metade do perímetro.

$Área espaço igual a espaço reto p espaço. espaço reto a espaço$

Onde,
p é o semiperímetro (perímetro dividido por dois)
a é a medida do apótema.

Exemplo
Um hexágono regular com medida do lado igual a 4 cm e apótema $2 raiz quadrada de 3$ cm possui como área:

Resolução
A área pode ser calculada como o produto entre o apótema e o semiperímetro.

Como um hexágono possui 6 lados, o perímetro é 6.4 = 24 cm e, seu semiperímetro 24/2 = 12 cm.

Portanto, a área é

$reto p espaço. espaço reto a espaço igual a espaço 12 espaço. espaço 2 raiz quadrada de 3 espaço espaço igual a espaço 24 raiz quadrada de 3 espaço cm ao quadrado espaço$

Veja mais sobre área e perímetro.

Exercícios de polígonos regulares

Exercício 1

Classifique os polígonos como regulares e não regulares.

Ver Resposta

A : não regular.
B : não regular.
C : regular.
D : regular.
E : não regular.
F : regular.

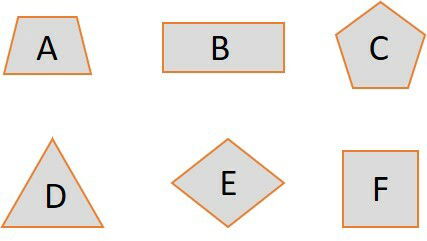
Exercício 2

Determine a soma dos ângulos internos de um polígono regular de 10 lados e a medida de cada ângulo.

Ver Resposta

A soma dos ângulos é determinada por:

$S com i subscrito igual a 180 espaço. espaço parêntese esquerdo n menos 1 parêntese direito S com i subscrito igual a 180 espaço. espaço parêntese esquerdo 10 menos 1 parêntese direito S com i subscrito igual a 180 espaço. espaço 9 S com i subscrito igual a 1.620 sinal de grau$

Como o polígono é regular, para determinar a medida dos ângulos, basta dividir o total por 10.

$a com i subscrito igual a S com i subscrito sobre n igual a 1620 sobre 10 igual a 162 sinal de grau$

Exercício 3

Calcule a área de um triângulo equilátero de lado igual a $8 raiz quadrada de 3$ cm e apótema igual 4 cm.

Ver Resposta

O perímetro do triângulo é: $8 raiz quadrada de 3 espaço. espaço 3 espaço igual a espaço 24 raiz quadrada de 3 espaço c m$ .

Seu semiperímetro é: $24 raiz quadrada de 3 espaço dividido por espaço 2 espaço igual a espaço 12 raiz quadrada de 3 espaço c m.$

Sua área é o produto do apótema pelo semiperímetro.

$reto A igual a reto p espaço. espaço reto a reto A igual a 12 raiz quadrada de 3 espaço. espaço 4 reto A igual a 48 raiz quadrada de 3 espaço cm ²$

Veja mais em:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.