Prisma - Figura Geométrica

Rosimar Gouveia

Professora de Matemática e Física

O prisma é um sólido geométrico que faz parte dos estudos de geometria espacial.

É caracterizado por ser um poliedro convexo com duas bases (polígonos iguais) congruentes e paralelas, além das faces planas laterais (paralelogramos).

Composição do Prisma

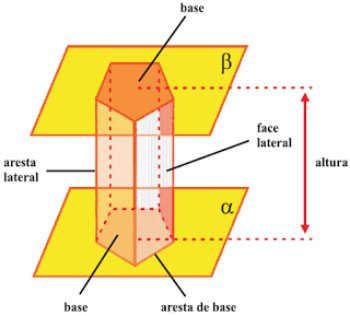
Os elementos que compõem o prisma são: base, altura, arestas, vértices e faces laterais.

Assim, as arestas das bases do prisma são os lados das bases do polígono, enquanto as arestas laterais correspondem aos lados das faces que não pertencem às bases.

Os vértices do prisma são os pontos de encontro das arestas e a altura é calculada pela distância entre os planos das bases.

Saiba mais sobre a Geometria Espacial.

Classificação dos Prismas

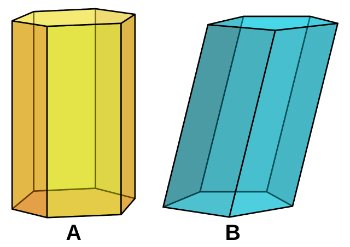
Os prismas são classificados em Retos e Oblíquos:

• Prisma Reto: possui arestas laterais perpendiculares à base, cujas faces laterais são retângulos.
• Prisma Oblíquo: possui arestas laterais oblíquas à base, cujas faces laterais são paralelogramos.

Conheça outros Poliedros.

Bases do Prisma

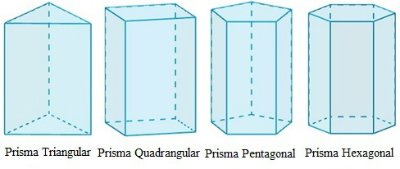
De acordo com o formato das bases, os primas são classificados em:

• Prisma Triangular: base formada por triângulo.
• Prisma Quadrangular: base formada por quadrado.
• Prisma Pentagonal: base formada por pentágono.
• Prisma Hexagonal: base formada por hexágono.
• Prisma Heptagonal: base formada por heptágono.
• Prisma Octogonal: base formada por octógono.

Os chamados “prismas regulares” são aqueles cujas bases são polígonos regulares e, portanto, formados por prismas retos.

Note que se todas as faces do prisma forem quadradas, trata-se de um cubo; se todas as faces forem paralelogramos, o prisma é um paralelepípedo.

Leia sobre as Formas Geométricas.

Fique Atento!

Para calcular a área da base (A_b) de um prisma deve-se levar em conta o formato que apresenta. Por exemplo, se for um prisma triangular a área da base será um triângulo.

Saiba mais sobre o cálculo da área:

• Área do Triângulo
• Área do Losango
• Área do Hexágono
• Área do Cubo

Fórmulas do Prisma

Áreas do Prisma

Área Lateral: para calcular a área lateral do prisma, basta somar as áreas das faces laterais. Num prisma reto, que possui todas as áreas das faces laterais congruentes, a fórmula da área lateral é:

A_l = n . a

n: número de lados
a: face lateral

Área Total: para calcular a área total de um prisma, basta somar as áreas das faces laterais e as áreas das bases:

A_t = S_l+ 2S_b

S_l: Soma das áreas das faces laterais
S_b: soma das áreas das bases

Volume do Prisma

O volume do prisma é calculado pela seguinte fórmula:

V = A_b.h

A_b: área da base
h: altura

Exercícios Resolvidos

Questão 1

Indique se as sentenças abaixo são verdadeiras (V) ou falsas (F):

a) O prisma é uma figura da geometria plana
b) Todo paralelepípedo é um prisma reto
c) As arestas laterais de um prisma são congruentes
d) As duas bases de um prisma são polígonos semelhantes
e) As faces laterais de um prisma oblíquo são paralelogramos

Questão 2

O número de faces laterais, arestas e vértices de um prisma oblíquo quadrangular é:

a) 6; 8; 12
b) 2; 8; 4
c) 2; 4; 8
d) 4; 10; 8
e) 4; 12; 8

Questão 3

O número de faces laterais, arestas e vértices de um prisma reto heptagonal é:

a) 7; 21; 14
b) 7; 12; 14
c) 14; 21; 7
d) 14; 7; 12
e) 21; 12; 7

Questão 4

Calcule a área da base, a área lateral e a área total de um prisma reto que apresenta 20 cm de altura, cuja base é um triângulo retângulo com catetos que medem 8 cm e 15 cm.

Questão 5

(Enem-2012) Maria quer inovar sua loja de embalagens e decidiu vender caixas com diferentes formatos. Nas imagens apresentadas estão as planificações dessas caixas.

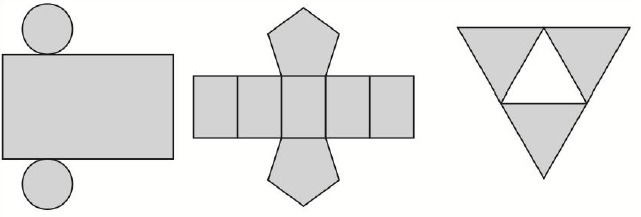
Quais serão os sólidos geométricos que Maria obterá a partir dessas planificações?

a) Cilindro, prisma de base pentagonal e pirâmide
b) Cone, prisma de base pentagonal e pirâmide
c) Cone, tronco de pirâmide e prisma
d) Cilindro, tronco de pirâmide e prisma
e) Cilindro, prisma e tronco de cone

Leia também sobre:

• Cubo
• Cone
• Cilindro
• Pirâmide
• Paralelepípedo
• Relação de Euler: vértices, faces e arestas

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.