Relação de Euler: vértices, faces e arestas
A relação de Euler é uma igualdade que relaciona o número de vértices, arestas e faces em poliedros convexos. Ela diz que o número de faces mais o de vértices é igual ao número de arestas mais dois.
A relação de Euler é dada por:
Onde,
- F é o número de faces;
- V o número de vértices;
- A o número de arestas.
Podemos utilizar a relação de Euler para determinar ou confirmar valores desconhecidos de V, F ou A, sempre que o poliedro for convexo.
| Poliedro | F | V | A | F + V | A + 2 |
|---|---|---|---|---|---|
| Cubo | 6 | 8 | 12 | 6 + 8 = 14 | 12 + 2 = 14 |
| Pirâmide triangular | 4 | 4 | 6 | 4 + 4 = 8 | 6 + 2 = 8 |
| Prisma de base pentagonal | 7 | 10 | 15 | 7 + 10 = 17 | 15 + 2 = 17 |
| Octaedro regular | 8 | 6 | 12 | 8 + 6 = 14 | 12 + 2 = 14 |
Exemplo:
Um poliedro convexo possui 20 faces e 12 vértices. Determine o número de arestas.
Resolução:
Utilizando a relação de Euler e isolando A:
Substituindo os valores de F e V:
Faces, vértices e arestas
Os poliedros são sólidos, formas geométricas de três dimensões sem lados arredondados. Estes lados são as faces (F) do poliedro.

Ao encontro das faces, damos o nome de arestas (A).

Os vértices são os pontos em que três ou mais arestas se encontram.
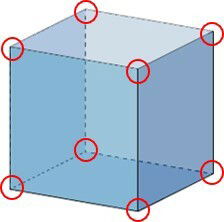
Poliedros convexos e não convexos
Os poliedros convexos são sólidos geométricos que não apresentam concavidade, por isso, em nenhuma de suas faces há ângulos internos maiores que 180º.
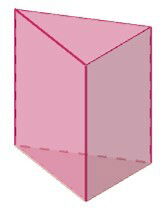
Os não convexos apresentam em suas faces pelo menos um ângulo interno maior que 180º.
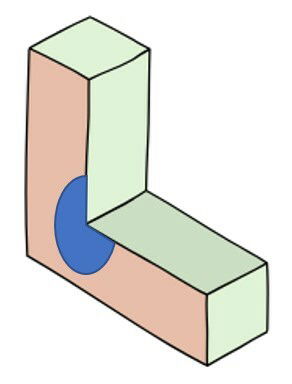
Neste poliedro, o ângulo interno marcado em azul possui mais de 180º, de forma que não é um poliedro convexo.
Veja mais sobre poliedros.
Exercícios sobre relação de Euler
Exercício 1
Determine o número de faces em um poliedro com 9 arestas e 6 vértices.
Exercício 2
Um dodecaedro é um sólido platônico com 12 faces. Sabendo que ele possui 20 vértices, determine seu número de arestas.
Exercício 3
Qual o nome do poliedro com 4 vértices e 6 arestas em relação ao seu número de faces, onde as faces são triângulos equiláteros?
Quem foi Leonhard Paul Euler?
Leonhard Paul Euler (1707-1783) foi um dos mais proficientes matemáticos e físicos da história, além de contribuir com estudos sobre Astronomia. Suíço de língua alemã, foi professor de Física da Academia de Ciências de São Petersburgo e, posteriormente, de Academia de Berlim. Publicou diversos estudos sobre Matemática.
Veja também: Sólidos geométricos
Para praticar:
Exercícios sobre a relação de Euler (com gabarito resolvido)
Exercícios sobre poliedros (com gabarito resolvido)
Exercícios de geometria espacial (com questões resolvidas)
ASTH, Rafael. Relação de Euler: vértices, faces e arestas. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/relacao-de-euler/. Acesso em:


