Retângulo: tudo sobre este polígono

Rafael C. Asth

Professor de Matemática e Física

O retângulo é uma figura geométrica plana formada por quatro lados (quadrilátero) e apresenta os quatro ângulos internos congruentes (mesma medida) e retos (90°).

Além disso, seus lados opostos são paralelos, por isso, o retângulo é um paralelogramo. Quando seus lados tiverem mesma medida, ele também será um quadrado. Ou seja, um quadrado é um retângulo especial.

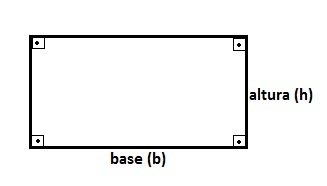
Retângulo

Área do Retângulo

Para encontrar a área da superfície de um retângulo, basta multiplicar o valor da base pelo da altura.

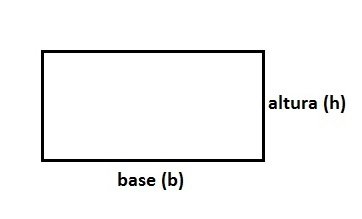
Assim, a fórmula da área do retângulo é expressa da seguinte forma:

$começar estilo tamanho matemático 20px reto A espaço igual a espaço reto b espaço. espaço reto h fim do estilo$

Donde,

A: área
b: base
h: altura

Perímetro do Retângulo

Já o conceito de perímetro é determinado pela soma de todos os lados da figura. Como os lados paralelos do retângulo apresentam mesma medida, seu perímetro será igual a soma de duas vezes o valor da base e da altura.

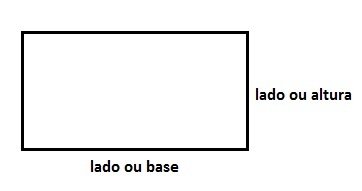
É expresso pela fórmula:

$começar estilo tamanho matemático 20px reto P espaço igual a espaço 2 parêntese esquerdo reto b espaço mais espaço reto h parêntese direito fim do estilo$

Ou, simplesmente:

$começar estilo tamanho matemático 20px reto P espaço igual a espaço reto b espaço mais espaço reto b espaço mais espaço reto h espaço mais espaço reto h reto P espaço igual a espaço 2 reto b espaço mais espaço 2 reto h fim do estilo$

Onde,

P é o perímetro;
b é a base;
h é a altura.

Para saber mais, leia também:

Diagonal do Retângulo

Quando traçamos uma diagonal no retângulo, ela formará dois triângulos retângulos. Assim, para calcular a diagonal do retângulo utilizamos o Teorema de Pitágoras.

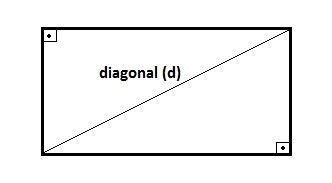
Note que a diagonal corresponde a hipotenusa do triângulo retângulo. Logo, a fórmula da diagonal do retângulo é expressa da seguinte forma:

$começar estilo tamanho matemático 20px reto d ao quadrado espaço igual a espaço reto b ao quadrado espaço mais espaço reto h ao quadrado espaço ou reto d espaço igual a espaço raiz quadrada de reto b ao quadrado mais reto h ao quadrado fim da raiz fim do estilo$

Donde,

d: diagonal
b: base
h: altura

Fique Atento!

Quando calculamos a área ou perímetro devemos considerar as unidades de medida. Ou seja, os valores devem estar na mesma unidade: centímetros, centímetros quadrados, metros, metro quadrados, etc.

Saiba mais sobre a Geometria Plana.

Retângulo Áureo

O retângulo áureo ou retângulo de ouro é um conceito da geometria euclidiana, o qual é também aplicado no campo das artes.

Trata-se de um caso de retângulo em que ao dividir a base pela sua altura, obtém-se o valor de aproximadamente 1,618. Esse número é chamado de número de ouro.

Exercícios de retângulos

Exercício 1

Calcule a área do retângulo que tem 5 cm de base e 3 cm de altura:

Ver Resposta

Nesse caso, aplica-se a fórmula da área:

A = b . h
A = 5 . 3
A = 15 cm²

Exercício 2

Indique se as sentenças abaixo são verdadeiras (V) ou falsas (F):

a) O retângulo é uma figura geométrica espacial.
b) A soma dos ângulos internos de um retângulo é 360º.
c) O retângulo é um quadrilátero.
d) Todo retângulo possui quatro lados iguais.
e) Todo quadrado é um retângulo.

Ver Resposta

a) F
b) V
c) V
d) F
e) V

Você Sabia?

Todos os retângulos são paralelogramos, mas nem todo paralelogramo é um retângulo. Assim como, os quadrados são retângulos, todavia, nem todos os retângulos são quadrados.

Triângulo Retângulo

O triângulo é uma figura geométrica plana formada por três lados. O triângulo retângulo é uma figura que também faz parte da geometria plana. Recebe esse nome, ao apresentar um ângulo reto, ou seja, de 90°.

Saiba mais sobre os triângulos com a leitura dos artigos:

Trapézio Retângulo

O trapézio é uma figura geométrica plana que possui quatro lados e bases paralelas, donde uma é maior e outra menor.

Da mesma forma que os triângulos retângulos, o chamado trapézio retângulo recebe esse nome, ao possuir dois ângulos retos de 90°.

Saiba também sobre a Área do Trapézio.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.