Segmento de Reta: o que é, tipos e exercícios

O segmento de reta é definido como parte da reta, sendo é um pedaço de reta. Ele é imitado por dois pontos.

Geralmente, os segmentos de reta são representados em colchetes, como: segmento de reta [AB]. Também, é possível representar um segmento de reta com um traço acima das letras: .

Diferença entre Segmento de Reta, Semirreta e Reta

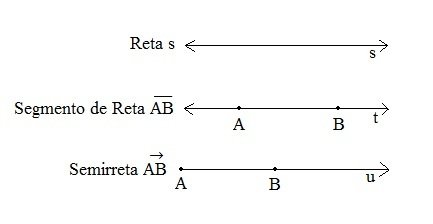
Lembre-se que retas são linhas não curvas infinitas e, portanto, são representadas por setas nos dois sentidos. Elas são indicadas por letras minúsculas (r, s, t).

Já os segmentos de reta são delimitados por dois pontos distantes na reta, os quais são indicados por letras maiúsculas. Na figura acima, os pontos A e B são chamados de extremidades do segmento de reta.

Por outro lado, as semirretas são ilimitadas num sentido, uma vez que possuem um ponto de origem e não possuem um ponto final. Assim, semirreta é a metade da reta, limitada por um ponto. Por esse motivo, apresentam uma seta que indica a direção em que ela é infinita.

Veja mais sobre:

• Retas
• Semirretas

Tipos de Segmentos de Reta

Segundo a posição que ocupam no plano, os segmentos de reta são classificados em:

Segmentos Consecutivos: quando possuem um ponto em comum. Na figura abaixo o ponto em comum é o D.

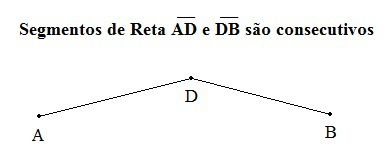
Segmentos Colineares: quando os pontos pertencem à mesma reta. Ou seja, quando dois ou mais pontos distintos compartilham a mesma reta.

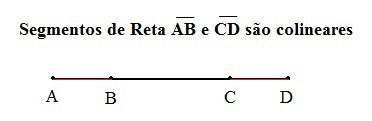
Segmentos Adjacentes: quando são consecutivos e lineares. Ou seja, possuem pontos em comum e por eles passa uma única reta.

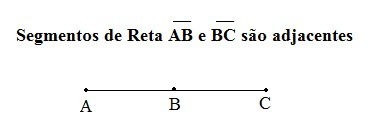
Segmentos Congruentes: quando dois segmentos apresentam a mesma medida. Na figura abaixo AB~CD (Lê-se: o segmento AB é congruente ao segmento CD).

Ponto Médio do Segmento de Reta

O ponto médio de um segmento de reta define o meio do segmento.

No exemplo a seguir, percebemos que M é o ponto médio do segmento de reta AB, donde AM~MB (Lê-se: o segmento AM é congruente com o segmento MB)

Saiba mais sobre:

• Formas Geométricas
• Retas Paralelas
• Distância entre dois pontos
• Equação da Reta
• Geometria Plana
• Geometria Espacial
• Geometria analítica

Exercícios sobre segmento de reta

Exercício 1

Quantos segmentos de reta possui um cubo?

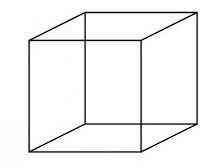
a) 4
b) 8
c) 10
d) 12
e) 14

Exercício 2

Quantos segmentos de reta possui o tetraedro e o triângulo?

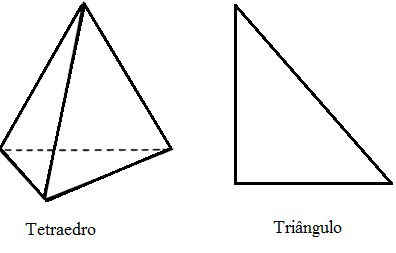
a) 6 e 3
b) 9 e 3
c) 10 e 3
d) 12 e 6
e) 14 e 6

Exercício 3

Observe a reta numérica abaixo:

Sabendo que:

• O ponto A representa o número 2.
• O ponto C representa o número 8.

Qual é o comprimento do segmento AB se o ponto B está exatamente no meio entre A e C?

Exercício 4

Na mesma reta numérica, se o ponto D estiver localizado a 7 unidades à direita de B, qual número representará a medida do segmento em unidades?