Simulado de Matemática e suas Tecnologias (ENEM)
Estude para o Enem com nosso simulado de Matemática. São 45 questões resolvidas e comentadas de Matemática e suas Tecnologias, selecionadas conforme os assuntos mais cobrados no Exame Nacional do Ensino Médio.
Atenção às regras do simulado
- 4545 questões
- Duração máxima de 3h
- Seu resultado e o gabarito ficarão disponíveis ao finalizar o simulado
Questão 1
Um construtor precisa revestir o piso de uma sala retangular. Para essa tarefa, ele dispõe de dois tipos de cerâmicas:
a) cerâmica em forma de quadrado de lado 20 cm, que custa R$ 8,00 por unidade;
b) cerâmica em forma de triângulo retângulo isósceles de catetos com 20 cm, que custa R$ 6,00 por unidade.
A sala tem largura de 5 m e comprimento de 6 m.
O construtor deseja gastar a menor quantia possível com a compra de cerâmica. Sejam x o número de peças de cerâmica de forma quadrada e y o número de peças de cerâmica de forma triangular.
Isso significa, então, encontrar valores para x e y tais que 0,04x + 0,02y > 30 e que tornem o menor possível valor de
A expressão do preço depende da quantidade x de revestimentos quadrados de R$ 8,00 mais y revestimentos triangulares de R$ 6,00.
8 . x + 6 . y
8x + 6y
Questão 2
Um grupo sanguíneo, ou tipo sanguíneo, baseia-se na presença ou ausência de dois antígenos, A e B, na superfície das células vermelhas do sangue. Como dois antígenos estão envolvidos, os quatro tipos sanguíneos distintos são:
• Tipo A: apenas o antígeno A está presente;
• Tipo B: apenas o antígeno B está presente;
• Tipo AB: ambos os antígenos estão presentes;
• Tipo O: nenhum dos antígenos está presente.
Foram coletadas amostras de sangue de 200 pessoas e, após análise laboratorial, foi identificado que em 100 amostras está presente o antígeno A, em 110 amostras há presença do antígeno B e em 20 amostras nenhum dos antígenos está presente. Dessas pessoas que foram submetidas à coleta de sangue, o número das que possuem o tipo sanguíneo A é igual a
Esta é uma questão sobre conjuntos.
Considere o conjunto universo com 200 elementos.

Destes 20 são do tipo O. Assim, 200 - 20 = 180, podem ser A, B ou AB.

Há 100 portadores do antígeno A e 110 do B. Como 100 + 110 = 210, deve haver uma intersecção, pessoas com sangue AB.
Esta intersecção deve possuir, 210 - 180 = 30 indivíduos, do tipo AB.
Dos 100 portadores do antígeno A, restam 100 - 30 = 70 pessoas apenas com antígeno A.
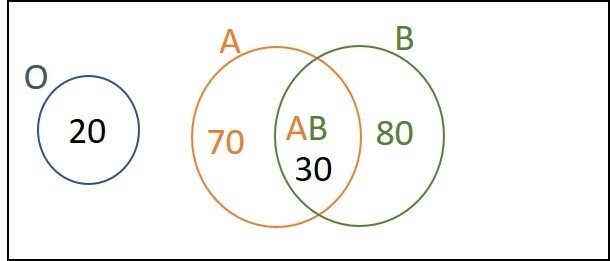
Conclusão
Portanto, 70 pessoas possuem sangue do tipo A.
Questão 3
Uma empresa especializou-se no aluguel de contêineres que são utilizados como unidades comerciais móveis. O modelo padrão alugado pela empresa tem altura de 2,4 m e as outras duas dimensões (largura e comprimento), 3,0 m e 7,0 m, respectivamente.
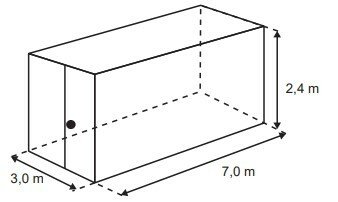
Um cliente solicitou um contêiner com altura padrão, porém, com largura 40% maior e comprimento 20% menor que as correspondentes medidas do modelo padrão. Para atender às necessidades de mercado, a empresa também disponibiliza um estoque de outros modelos de contêineres, conforme o quadro.
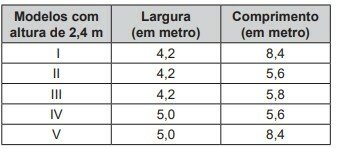
Dos modelos disponíveis, qual atende às necessidades do cliente?
Largura 40% maior.
Para aumentar 40% basta multiplicar por 1,40.
1,40 x 3,0 = 4,2 m
Comprimento 20% menor
Para diminuir 20% basta multiplicar por 0,80.
0,80 x 7,0 = 5,6 m
Conclusão
O modelo II atende às necessidades do cliente.
4,2 m de largura e 5,6 m de comprimento.
Questão 4
Dois atletas partem de pontos, respectivamente P1 e P2 , em duas pistas planas distintas, conforme a figura, deslocando-se no sentido anti-horário até a linha de chegada, percorrendo, desta forma, a mesma distância (L). Os trechos retos dos finais das curvas até a linha de chegada desse percurso têm o mesmo comprimento (l) nas duas pistas e são tangentes aos trechos curvos, que são semicírculos de centro C. O raio do semicírculo maior é R1 e o raio do semicírculo menor é R2 .
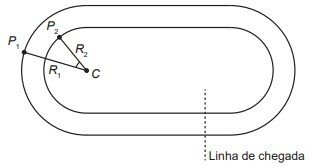
Sabe-se que o comprimento de um arco circular é dado pelo produto do seu raio pelo ângulo, medido em radiano, subentendido pelo arco. Nas condições apresentadas, a razão da medida do ângulo pela diferença L− l é dada por
Objetivo
Determinar a razão
Dados
L é o comprimento total e é o mesmo para os dois atletas.
l é o comprimento da parte reta e é o mesmo para os dois atletas.
Passo 1: Determinar
Chamando o ângulo do atleta 1 e
o ângulo do atleta 2, o ângulo
é a diferença entre os dois.
Como dito no enunciado, o arco é o produto entre o raio e o ângulo.
Substituindo na equação anterior:
Passo 2: Determinar L - l
Chamando d1 a distância curva percorrida pelo atleta 1, ele percorre no total:
L = d1 + l
Chamando d2 a distância curva percorrida pelo atleta 2, ele percorre no total:
L = d2 + l
Isto implica que d1 = d2, pois como l e L são os mesmos para os dois atletas, as distâncias curvas também devem ser iguais. Logo
d1 = L - l
d2 = L - l
E, d1 = d2
Passo 3: determinar a razão
Substituindo d1 por d2,
Conclusão
A resposta é 1/R2 - 1/R1.
Questão 5
Um vaso decorativo quebrou e os donos vão encomendar outro para ser pintado com as mesmas características. Eles enviam uma foto do vaso na escala 1 : 5 (em relação ao objeto original) para um artista. Para ver melhor os detalhes do vaso o artista solicita uma cópia impressa da foto com dimensões triplicadas em relação às dimensões da foto original. Na cópia impressa, o vaso quebrado tem uma altura de 30 centímetros.
Qual é a altura real, em centímetros, do vaso quebrado?
Objetivo
Determinar a altura real do vaso.
Chamando a altura original de h
Primeiro momento: foto
A foto enviada está na escala 1 : 5, o que significa dizer que é cinco vezes menor que o vaso.
Nesta foto, a altura é 1/5 da altura real.
Segundo momento: cópia impressa ampliada
A cópia impressa é triplicada em dimensões (3 : 1), o que significa ser 3 vezes maior que a foto.
Na cópia, a altura é 3 vezes maior que na foto e possui 30 cm.
Conclusão
O vaso original possui 50 cm de altura.
Questão 6
Após o término das inscrições de um concurso, cujo número de vagas é fixo, foi divulgado que a razão entre o número de candidatos e o número de vagas, nesta ordem, era igual a 300. Entretanto, as inscrições foram prorrogadas, inscrevendo-se mais 4 000 candidatos, fazendo com que a razão anteriormente referida passasse a ser igual a 400. Todos os candidatos inscritos fizeram a prova, e o total de candidatos aprovados foi igual à quantidade de vagas. Os demais candidatos foram reprovados.
Nessas condições, quantos foram os candidatos reprovados?
Objetivo
Determinar o número de reprovados.
Passo 1: número de reprovados.
R = TC - V
Sendo,
R o número de reprovados;
TC o total de candidatos;
V o número de vagas (aprovados).
O total de candidatos TC, é o número inicial de candidatos inscritos C, mais 4000.
TC = C + 4000
Assim, o número de reprovados é:
Passo 2: primeiro momento da inscrição.
Logo, C = 300V
Passo 3: segundo momento da inscrição.
Substituindo o valor de C e isolando V.
Substituindo V = 40 em C = 300V.
C = 300 . 40 = 12 000
Temos,
V = 40 (total de vagas ou candidatos aprovados)
C = 12 000
Substituindo na equação do passo 1:
Conclusão
15 960 candidatos foram reprovados no concurso.
Questão 7
No trapézio isósceles mostrado na figura a seguir, M é o ponto médio do segmento BC, e os pontos P e Q são obtidos dividindo o segmento AD em três partes iguais.
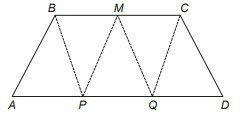
Pelos pontos B, M, C, P e Q são traçados segmentos de reta, determinando cinco triângulos internos ao trapézio, conforme a figura. A razão entre BC e AD que determina áreas iguais para os cinco triângulos mostrados na figura é
Os cinco triângulos possuem a mesma área e a mesma altura, pois a distância entre as bases do trapézio são iguais em qualquer ponto, visto que BC e AD são paralelas.
Como a área de um triângulo é determinada por e todos possuem mesma área, isto implica que as bases também são iguais a todos.
Assim, BC = 2b e Ad = 3b
Logo, a razão é:
Questão 8
Um parque temático brasileiro construiu uma réplica em miniatura do castelo de Liechtenstein. O castelo original, representado na imagem, está situado na Alemanha e foi reconstruído entre os anos de 1840 e 1842, após duas destruições causadas por guerras.

O castelo possui uma ponte de 38,4 m de comprimento e 1,68 m de largura. O artesão que trabalhou para o parque produziu a réplica do castelo, em escala. Nessa obra, as medidas do comprimento e da largura da ponte eram, respectivamente, 160 cm e 7 cm.
A escala utilizada para fazer a réplica é
A escala é O : R
Sendo O a medida original e R da réplica.
Tomando a medida do comprimento:
Logo, a escala é de 1 : 24.
Questão 9
Um mapa é a representação reduzida e simplificada de uma localidade. Essa redução, que é feita com o uso de uma escala, mantém a proporção do espaço representado em relação ao espaço real.
Certo mapa tem escala 1 : 58 000 000.
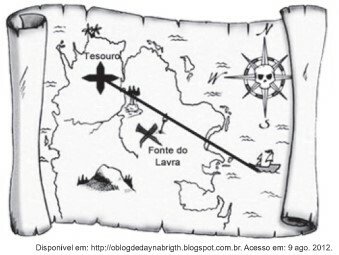
Considere que, nesse mapa, o segmento de reta que liga o navio à marca do tesouro meça 7,6 cm.
A medida real, em quilômetro, desse segmento de reta é
A escala do mapa é 1 : 58 000 000
Isto significa que 1 cm no mapa equivalem 58 000 000 cm no terreno real.
Passando para quilômetro, dividimos por 100 000.
58 000 000 / 100 000 = 580 km.
Montando a proporção:
Questão 10
O quadro apresenta a relação dos jogadores que fizeram parte da seleção brasileira de voleibol masculino nas Olimpíadas de 2012, em Londres, e suas respectivas alturas, em metro.
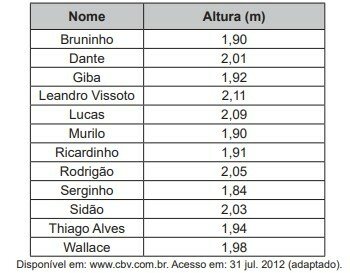
A mediana das alturas, em metro, desses jogadores é
A mediana é uma medida de tendência central e, é necessário organizar os dados de maneira crescente.

Como a quantidade de dados é par (12), a mediana é a média aritmética das medidas centrais.
Questão 11
Uma empresa aérea lança uma promoção de final de semana para um voo comercial. Por esse motivo, o cliente não pode fazer reservas e as poltronas serão sorteadas aleatoriamente. A figura mostra a posição dos assentos no avião:
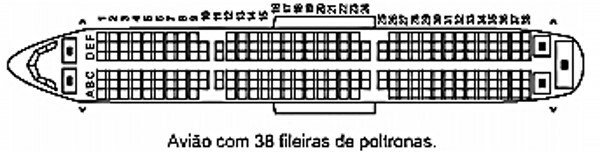
Por ter pavor de sentar entre duas pessoas, um passageiro decide que só viajará se a chance de pegar uma dessas poltronas for inferior a 30%.
Avaliando a figura, o passageiro desiste da viagem, porque a chance de ele ser sorteado com uma poltrona entre duas pessoas é mais aproximada de
A probabilidade é uma razão entre a quantidade de casos favoráveis e a quantidade total.
Total de poltronas
O total de poltronas no avião é:
38 x 6 - 8 = 220 poltronas.
Repare de há 8 espaços sem poltronas.
Poltronas desconfortáveis
38 x 2 (as que estão entre duas) menos 8, que possuem espaços vazios perto das janelas.
38 x 2 - 8 = 68
A probabilidade é:
Em porcentagem
0,3090 x 100 = 30,9%
Conclusão
A probabilidade do passageiro se sentar entre duas pessoas é de, aproximadamente, 31%.
Questão 12
O Índice de Desenvolvimento Humano (IDH) mede a qualidade de vida dos países para além dos indicadores econômicos. O IDH do Brasil tem crescido ano a ano e atingiu os seguintes patamares: 0,600 em 1990; 0,665 em 2000; 0,715 em 2010. Quanto mais perto de 1,00, maior é o desenvolvimento do país.
O Globo. Caderno Economia, 3 nov. 2011 (adaptado).
Observando o comportamento do IDH nos períodos citados, constata-se que, ao longo do período 1990-2010, o IDH brasileiro
A variação entre 2000 e 1990 foi de:
IDH 2000 - IDH 1990
0,665 - 0,600 = 0,065
A variação entre 2010 e 2000 foi de:
IDH 2010 - IDH 2000
0,715 - 0,665 = 0,050
Sendo assim o IDH aumentou com variações decenais decrescentes.
Questão 13
Um contrato de empréstimo prevê que quando uma parcela é paga de forma antecipada, conceder-se-á uma redução de juros de acordo com o período de antecipação. Nesse caso, paga-se o valor presente, que é o valor, naquele momento, de uma quantia que deveria ser paga em uma data futura. Um valor presente P submetido a juros compostos com taxa i, por um período de tempo n, produz um valor futuro V determinado pela fórmula
Em um contrato de empréstimo com sessenta parcelas fixas mensais, de R$ 820,00, a uma taxa de juros de 1,32% ao mês, junto com a trigésima parcela será paga antecipadamente uma outra parcela, desde que o desconto seja superior a 25% do valor da parcela.
Utilize 0,2877 como aproximação para e 0,0131 como aproximação para In (1,0132).
A primeira das parcelas que poderá ser antecipada junto com a 30ª é a
Objetivo
Calcular o número da parcela que deve ser antecipada para produzir 25% de desconto no valor presente.
O número da parcela é 30 + n. Onde 30 é o número da parcela atual e n é o número de parcelas à frente necessário.
V é o valor da parcela, R$820,00.
P é o valor da parcela adiantada.
i é a taxa 1,32% = 0,0132
n é o número de parcelas
O valor a ser pago na parcela antecipada deve ser, pelo menos, 25% menor que o valor de R$820,00.
Da fórmula de juros compostos fornecida pela questão, temos:
Aplicando o logarítmo em ambos os lados da igualdade:
Pela propriedade dos logarítmos, o expoente n passa a multiplicar o logarítmo.
Substituindo os valores fornecidos na questão:
Assim, acrescentando 22 + 30 = 52.
Conclusão
A parcela adiantada deve ser a 52ª.
Questão 14
Camile gosta de caminhar em uma calçada em torno de uma praça circular que possui 500 metros de extensão, localizada perto de casa. A praça, bem como alguns locais ao seu redor e o ponto de onde inicia a caminhada, estão representados na figura:
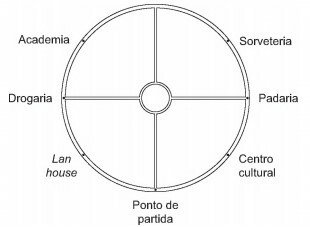
Em uma tarde, Camile caminhou 4 125 metros, no sentido anti-horário, e parou.
Qual dos locais indicados na figura é o mais próximo de sua parada?
O enunciado diz que uma volta possui 500 m. É preciso cuidado para não confundir extensão com diâmetro.
Após 8 voltas completas ela para no ponto de partida novamente, e avança mais 1/4 de volta no sentido anti-horário, chegando na padaria.
Questão 15
O prefeito de uma cidade deseja promover uma festa popular no parque municipal para comemorar o aniversário de fundação do município. Sabe-se que esse parque possui formato retangular, com 120 m de comprimento por 150 m de largura. Além disso, para segurança das pessoas presentes no local, a polícia recomenda que a densidade média, num evento dessa natureza, não supere quatro pessoas por metro quadrado.
Seguindo as recomendações de segurança estabelecidas pela polícia, qual é o número máximo de pessoas que poderão estar presentes na festa?
A área da praça é de 120 x 150 = 18 000 m².
Com 4 pessoas por metro quadrado, temos:
18 000 x 4 = 72 000 pessoas.
Questão 16
Um zootecnista pretende testar se uma nova ração para coelhos é mais eficiente do que a que ele vem utilizando atualmente. A ração atual proporciona uma massa média de 10 kg por coelho, com um desvio padrão de 1 kg, alimentado com essa ração durante um período de três meses.
O zootecnista selecionou uma amostra de coelhos e os alimentou com a nova ração pelo mesmo período de tempo. Ao final, anotou a massa de cada coelho, obtendo um desvio padrão de 1,5 kg para a distribuição das massas dos coelhos dessa amostra.
Para avaliar a eficiência dessa ração, ele utilizará o coeficiente de variação (CV) que é uma medida de dispersão definida por CV = , em que s representa o desvio padrão e
, a média das massas dos coelhos que foram alimentados com uma determinada ração.
O zootecnista substituirá a ração que vinha utilizando pela nova, caso o coeficiente de variação da distribuição das massas dos coelhos que foram alimentados com a nova ração for menor do que o coeficiente de variação da distribuição das massas dos coelhos que foram alimentados com a ração atual.
A substituição da ração ocorrerá se a média da distribuição das massas dos coelhos da amostra, em quilograma, for superior a
Para que ocorra substituição, a condição é:
CV nova < CV atual
Dados com a ração atual.
CV atual =
Dados com a ração nova.
Para determinar o x necessário para que ocorra a substituição:
Questão 17
O número de frutos de uma determinada espécie de planta se distribui de acordo com as probabilidades apresentadas no quadro.
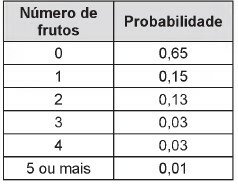
A probabilidade de que, em tal planta, existam, pelo menos, dois frutos é igual a
Pelo menos dois, implica haver dois ou mais.
P(2) ou P(3) ou P(4) ou P(5) = 0,13 + 0,03 +0,03 + 0,01 = 0,20 ou 20%
Questão 18
A taxa de urbanização de um município é dada pela razão entre a população urbana e a população total do município (isto é, a soma das populações rural e urbana). Os gráficos apresentam, respectivamente, a população urbana e a população rural de cinco municípios (I, II, III, IV, V) de uma mesma região estadual. Em reunião entre o governo do estado e os prefeitos desses municípios, ficou acordado que o município com maior taxa de urbanização receberá um investimento extra em infraestrutura.
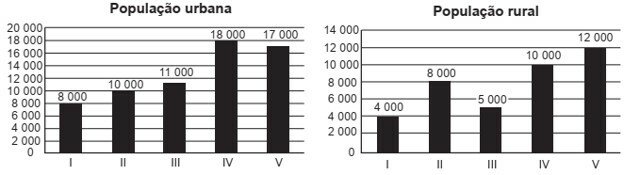
Segundo o acordo, qual município receberá o investimento extra?
A taxa de urbanização é dada por:
Verificando para cada município:
Município I
Município II
Município III
Município IV
Município V
Logo, a maior taxa de urbanização é a do município III.
Questão 19
A Lei da Gravitação, de Isaac Newton, estabelece a intensidade da força entre dois objetos. Ela é dada pela equaçao , sendo m1 e m2 as massas dos objetos, d a distância entre eles, g a constante universal da gravitação e F a intensidade da força gravitacional que um objeto exerce sobre o outro.
Considere um esquema que represente cinco satélites de mesma massa orbitando a Terra. Denote os satélites por A, B, C, D e E, sendo esta a ordem decrescente da distância da Terra (A o mais distante e E o mais próximo da Terra).
De acordo com a Lei da Gravitação Universal, a Terra exerce maior força sobre o satélite
Como na fórmula d está no denominador e quanto maior for seu valor, menor será a força, pois será uma divisão por um número maior. Desse modo, a força gravitacional diminui com o aumento da distância.
Assim, para um menor d, a força é maior.
Portanto, o satélite E e a Terra formam a maior força gravitacional.
Questão 20
Uma fábrica de tubos acondiciona tubos cilíndricos menores dentro de outros tubos cilíndricos. A figura mostra uma situação em que quatro tubos cilíndricos estão acondicionados perfeitamente em um tubo com raio maior.
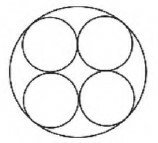
Suponha que você seja o operador da máquina que produzirá os tubos maiores em que serão colocados, sem ajustes ou folgas, quatro tubos cilíndricos internos.
Se o raio da base de cada um dos cilindros menores for igual a 6 cm, a máquina por você operada deverá ser ajustada para produzir tubos maiores, com raio da base igual a
Unindo os raios dos círculos menores formamos um quadrado:
O raio do círculo maior é a metade da diagonal deste quadrado mais um raio de um círculo menor.
Onde,
R é o raio do círculo maior.
d é a diagonal do quadrado.
r é o raio do círculo menor.
Para determinar a diagonal do quadrado, utilizamos o teorema de Pitágoras, onde a diagonal é a hipotenusa do triângulo com lados iguais a r + r = 12.
Substituindo o valor de d na equação de R, temos:
Igualando os denominadores,
Fatorando o 288, temos:
288 = 2 . 2² . 2² . 3²
A raíz de 288 fica:
Substituindo na equação do R:
Colocando o 12 em evidência e simplificando,
Questão 21
Uma pessoa produzirá uma fantasia utilizando como materiais: 2 tipos de tecidos diferentes e 5 tipos distintos de pedras ornamentais. Essa pessoa tem à sua disposição 6 tecidos diferentes e 15 pedras ornamentais distintas.
A quantidade de fantasias com materiais diferentes que podem ser produzidas é representada pela expressão
Pelo princípio multiplicativo temos que o número de possibilidades é o produto entre:
opções de tecidos x opções de pedras
Como serão escolhidos 2 tecidos entre 6, devemos saber de quantas formas podemos escolher 2 tecidos em um conjunto de 6 tecidos diferentes.
Em relação às pedras, iremos escolher 5 pedras em um conjunto de 15 diferentes, logo:
Sendo assim, a quantidade de fantasias com materiais diferentes que podem ser produzidas é representada pela expressão:
Questão 22
A probabilidade de um empregado permanecer em uma dada empresa particular por 10 anos ou mais é de 1/6.
Um homem e uma mulher começam a trabalhar nessa companhia no mesmo dia. Suponha que não haja nenhuma relação entre o trabalho dele e o dela, de modo que seus tempos de permanência na firma são independentes entre si.
A probabilidade de ambos, homem e mulher, permanecerem nessa empresa por menos de 10 anos é de
A probabilidade de permanecer mais de 10 anos é 1/6, logo, a probabilidade de permanecer menos de 10 anos é de 5/6, para cada funcionário.
Como queremos a probabilidade de que os dois saiam antes de 10 anos, temos:
Questão 23
Um vidraceiro é contratado para colocar uma porta de vidro que escorregará em uma canaleta de largura interna igual a 1,45 cm, como mostra a figura.
![]()
O vidraceiro precisa de uma placa de vidro de maior espessura possível, tal que deixe uma folga total de pelo menos 0,2 cm, para que o vidro possa escorregar na canaleta, e no máximo 0,5 cm para que o vidro não fique batendo com a interferência do vento após a instalação. Para conseguir essa placa de vidro, esse vidraceiro foi até uma loja e lá encontrou placas de vidro com espessuras iguais a: 0,75 cm; 0,95 cm; 1,05 cm; 1,20 cm; 1,40 cm.
Para atender às restrições especificadas, o vidraceiro deverá comprar a placa de espessura, em centímetro, igual a
Folga mínima
A espessura da canaleta, 1,45 cm, menos a espessura do vidro, devem permitir uma folga de pelo menos 0,20 cm.
1,45 - 0,20 = 1,25 cm
Folga máxima
A espessura da canaleta,1,45 cm, menos a espessura do vidro devem permitir uma folga de no máximo 0,50 cm.
1,45 - 0,50 = 0,95 cm
Assim, a espessura do vidro deve ser entre 0,95 e 1,25 cm, sendo a maior possível.
Conclusão
Dentre as opções, o vidro de 1,20 cm está no intervalo e é o maior disponível.
Questão 24
Um atleta produz sua própria refeição com custo fixo de R$ 10,00. Ela é composta por 400 g de frango, 600 g de batata-doce e uma hortaliça. Atualmente, os preços dos produtos para essa refeição são:

Em relação a esses preços, haverá um aumento de 50% no preço do quilograma de batata-doce, e os outros preços não serão alterados. O atleta deseja manter o custo da refeição, a quantidade de batata-doce e a hortaliça. Portanto, terá que reduzir a quantidade de frango.
Qual deve ser a redução percentual da quantidade de frango para que o atleta alcance seu objetivo?
Dados
Custo fixo
400 g de frango a R$12,50 o kg.
600 g batata-doce a R$ 5,00 kg.
1 hortaliça
Aumento de 50% no preço da batata-doce.
Objetivo
Determinar a redução percentual de frango na refeição que mantenha o preço após o aumento.
Custo atual
Transformando a massa de g para kg.
0,4 x 12,50 = R$ 5,00 de frango.
0,6 x 5,00 = R$ 3,00 de batata-doce.
R$ 2,00 da hortaliça.
Aumento no preço da batata-doce.
5,00 + 50% de 5,00
5,00 x 1,50 = R$ 7,50
Novo custo
0,6 x 7,5 = R$ 4,50 de batata-doce
R$ 2,00 da hortaliça.
O subtotal é de: 4,50 + 2,00 = 6,50.
Desse modo, sobram 10,00 - 6,50 = 3,50 para compra do frango.
Nova quantidade de frango
12,50 compram 1000g
3,50 comprar xg
Fazendo uma regra de três:
Redução percentual
Isto significa que houve uma redução de 0,30, pois, 1,00 - 0,70 = 0,30.
Conclusão
O atleta deverá reduzir a quantidade de frango em 30% para manter o preço da refeição.
Questão 25
Um técnico gráfico constrói uma nova folha a partir das medidas de uma folha A0. As medidas de uma folha A0 são 595 mm de largura e 840 mm de comprimento.
A nova folha foi construída do seguinte modo: acrescenta uma polegada na medida da largura e 16 polegadas na medida do comprimento. Esse técnico precisa saber a razão entre as medidas da largura e do comprimento, respectivamente, dessa nova folha.
Considere 2,5 cm como valor aproximado para uma polegada.
Qual é a razão entre as medidas da largura e do comprimento da nova folha?
Passando as medidas para milimetro:
Largura = 595 mm + (1 . 2,5 . 10) mm = 620 mm
Comprimento = 840 mm + (16 . 2,5 . 10) mm = 1 240 mm
A razão é:
620/1240
Questão 26
Na construção de um conjunto habitacional de casas populares, todas serão feitas num mesmo modelo, ocupando, cada uma delas, terrenos cujas dimensões são iguais a 20 m de comprimento por 8 m de largura. Visando a comercialização dessas casas, antes do início das obras, a empresa resolveu apresentá-las por meio de maquetes construídas numa escala de 1 : 200.
As medidas do comprimento e da largura dos terrenos, respectivamente, em centímetros, na maquete construída, foram de
Passando as medidas do terreno para centímetro:
20 m = 2000 cm
8 m = 800 cm
Como a escala é de 1:200 devemos dividir as medidas do terreno por 200.
2000 / 200 = 10
800 / 20 = 4
Conclusão
A resposta é: 10 e 4.
Questão 27
Para certas molas, a constante elástica (C) depende do diâmetro médio da circunferência da mola (D), do número de espirais úteis (N), do diâmetro (d) do fio de metal do qual é formada a mola e do módulo de elasticidade do material (G). A fórmula evidencia essas relações de dependência.
O dono de uma fábrica possui uma mola M1 em um de seus equipamentos, que tem características D1, d1, N1 e G1, com uma constante elástica C1. Essa mola precisa ser substituída por outra, M2, produzida com outro material e com características diferentes, bem como uma nova constante elástica C2, da seguinte maneira: I) D2 = D1/3 ; II) d2 = 3d1; III) N2 = 9N1. Além disso, a constante de elasticidade G2 do novo material é igual a 4 G1.
O valor da constante C2 em função da constante C1 é
A segunda mola é:
Os valores das constantentes 2 são:
D2 = D1/3
d2 = 3d1
N2 = 9N1
G2 = 4G1
Substituindo e fazendo os cálculos:
Passando os coeficientes para frente:
Podemos substituir por C1 e calcular o novo coeficiente.
Questão 28
O padrão internacional ISO 216 define os tamanhos de papel utilizados em quase todos os países. O formato-base é uma folha retangular de papel chamada de A0, cujas dimensões estão na razão 1 :√2 . A partir de então, dobra-se a folha ao meio, sempre no lado maior, definindo os demais formatos, conforme o número da dobradura. Por exemplo, A1 é a folha A0 dobrada ao meio uma vez, A2 é a folha A0 dobrada ao meio duas vezes, e assim sucessivamente, conforme figura.

Um tamanho de papel bastante comum em escritórios brasileiros é o A4, cujas dimensões são 21,0 cm por 29,7 cm.
Quais são as dimensões, em centímetros, da folha A0?
As dimensões da folha A0 são quatro vezes as dimensões da folha A4. Logo:
Questão 29
Um país decide investir recursos na educação em suas cidades que tenham um alto nível de analfabetismo. Os recursos serão divididos de acordo com a idade média da população que é analfabeta, conforme apresentado no quadro.
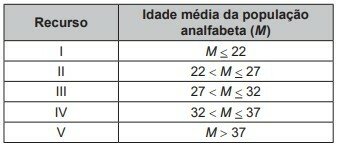
Uma cidade desse país possui 60/100 do total de analfabetos de sua população composto por mulheres. A média de idade das mulheres analfabetas é de 30 anos, e a média de idade dos homens analfabetos é de 35 anos.
Considerando a média de idade da população analfabeta dessa cidade, ela receberá o recurso
Trata-se de uma média ponderada.
De acordo com as opções, a resposta é a alternativa c.
Recurso III
Questão 30
Os alunos do curso de matemática de uma universidade desejam fazer uma placa de formatura, no formato de um triângulo equilátero, em que os seus nomes aparecerão dentro de uma região quadrada, inscrita na placa, conforme a figura.
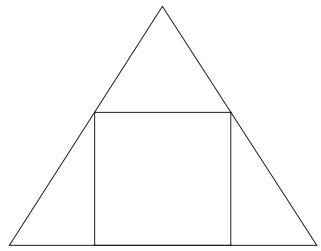
Considerando que a área do quadrado, em que aparecerão os nomes dos formandos, mede 1 m², qual é aproximadamente a medida, em metro, de cada lado do triângulo que representa a placa? (Utilize 1,7 como valor aproximado para √3 ).
Como o triângulo é equilátero os três lados são iguais e os ângulos internos iguais a 60º.
Como a área do quadrado é de 1 m², seus lados medem 1 m.
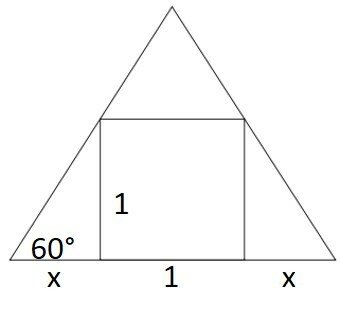
A base do triângulo é x + 1 + x, logo:
L = 2x + 1
Onde L é a medida do lado do triângulo.
A tangente de 60º é:
Como o enunciado fornece o valor aproximado da raiz de 3, vamos substituir na fórmula L = 2x + 1.
Questão 31
Uma construtora pretende conectar um reservatório central (Rc) em formato de um cilindro, com raio interno igual a 2 m e altura interna igual a 3,30 m, a quatro reservatórios cilíndricos auxiliares (R1, R2, R3 e R4), os quais possuem raios internos e alturas internas medindo 1,5 m.
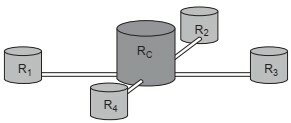
As ligações entre o reservatório central e os auxiliares são feitas por canos cilíndricos com 0,10 m de diâmetro interno e 20 m de comprimento, conectados próximos às bases de cada reservatório. Na conexão de cada um desses canos com o reservatório central há registros que liberam ou interrompem o fluxo de água.
No momento em que o reservatório central está cheio e os auxiliares estão vazios, abrem-se os quatro registros e, após algum tempo, as alturas das colunas de água nos reservatórios se igualam, assim que cessa o fluxo de água entre eles, pelo princípio dos vasos comunicantes.
A medida, em metro, das alturas das colunas de água nos reservatórios auxiliares, após cessar o fluxo de água entre eles, é
A altura da coluna de água será a mesma, incluindo no reservatório central.
Volume inicial no RC.
Uma parte deste volume irá escoar para os tubos e reservatórios menores, mas o volume no sistema continua o mesmo, antes e depois do escoamento.
Volume em Rc = 4 . volume nos canos + 4 . volume do reservatório + volume que sobrou em Rc
A altura pretendida é h.
Colocando em evidência, simplificando e resolvendo para h, temos:
Questão 32
Em um estudo realizado pelo IBGE em quatro estados e no Distrito Federal, com mais de 5 mil pessoas com 10 anos ou mais, observou-se que a leitura ocupa, em média, apenas seis minutos do dia de cada pessoa. Na faixa de idade de 10 a 24 anos, a média diária é de três minutos. No entanto, no grupo de idades entre 24 e 60 anos, o tempo médio diário dedicado à leitura é de 5 minutos. Entre os mais velhos, com 60 anos ou mais, a média é de 12 minutos.
A quantidade de pessoas entrevistadas de cada faixa de idade seguiu a distribuição percentual descrita no quadro.
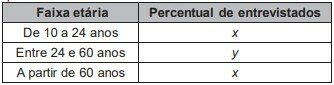
Disponível em: www.oglobo.globo.com. Acesso em: 16 ago. 2013 (adaptado).
Os valores de x e y do quadro são, respectivamente, iguais a
O percentual total de entrevistados é:
x + y + x = 100%
2x + y = 1 (equação I)
A média geral de leitura é de 6 min. Esta média é ponderada pelas quantidades x e y.
Substituindo na equação I
Substituindo o valor de x na equação I
Em termos percentuais,
x = 1/5 = 0,20 = 20%
y = 3/5 = 0,60 = 60%
Questão 33
Em março de 2011, um terremoto de 9,0 graus de magnitude na escala Richter atingiu o Japão matando milhares de pessoas e causando grande destruição. Em janeiro daquele ano, um terremoto de 7,0 graus na escala Richter atingiu a cidade de Santiago Del Estero, na Argentina. A magnitude de um terremoto, medida pela escala Richter, é , em que A é a amplitude do movimento vertical do solo, informado em um sismógrafo, A0 é uma amplitude de referência e log representa o logaritmo na base 10.
Disponível em: http://earthquake.usgs.gov. Acesso em: 28 fev. 2012 (adaptado).
A razão entre as amplitudes dos movimentos verticais dos terremotos do Japão e da Argentina é
O objetivo é determinar
Sendo a amplitude do terremoto do Japão e
a aplitude do terremoto na Argentina.
Da definição de logarítmo
Podemos escrever
Utilizando a definição de logarítmo na relação fornecida no enunciado:
Com,
b=10 (a base 10 não precisa estar escrita)
c = R
a = A/A0
Para o terremoto do Japão:
Para o terremoro da Argentina:
Igualando os valores de referência
Questão 34
Devido ao não cumprimento das metas definidas para a campanha de vacinação contra a gripe comum e o vírus H1N1 em um ano, o Ministério da Saúde anunciou a prorrogação da campanha por mais uma semana. A tabela apresenta as quantidades de pessoas vacinadas dentre os cinco grupos de risco até a data de início da prorrogação da campanha.
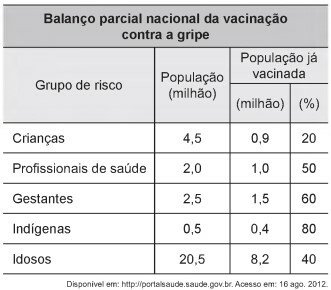
Qual é a porcentagem do total de pessoas desses grupos de risco já vacinadas?
O total da população de risco é: 4,5 + 2,0 + 2,5 + 0,5 + 20,5 = 30
O total já vacinado é: 0,9 + 1,0 + 1,5 + 0,4 + 8,2 = 12
Questão 35
Um ciclista quer montar um sistema de marchas usando dois discos dentados na parte traseira de sua bicicleta, chamados catracas. A coroa é o disco dentado que é movimentado pelos pedais da bicicleta, sendo que a corrente transmite esse movimento às catracas, que ficam posicionadas na roda traseira da bicicleta. As diferentes marchas ficam definidas pelos diferentes diâmetros das catracas, que são medidos conforme indicação na figura.
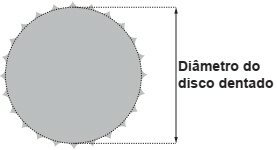
O ciclista já dispõe de uma catraca com 7 cm de diâmetro e pretende incluir uma segunda catraca, de modo que, à medida em que a corrente passe por ela, a bicicleta avance 50% a mais do que avançaria se a corrente passasse pela primeira catraca, a cada volta completa dos pedais.
O valor mais próximo da medida do diâmetro da segunda catraca, em centímetro e com uma casa decimal, é
O comprimento da circunferência é dado por:
O raio da primeira catraca é de 3,5 cm.
Para a primeira catraca temos: para uma volta.
Para a segunda, deve haver um aumento de 50% no avanço, ou, mais meia volta.
Se uma volta completa são , meia volta é
. Assim, uma volta e meia são
.
Com o mesmo gira de agora queremos que a bicicleta avance
.
Como o diâmetro são duas vezes o raio:
A alternativa mais próxima é a letra c) 4,7.
Questão 36
No desenvolvimento de um novo remédio, pesquisadores monitoram a quantidade Q de uma substância circulando na corrente sanguínea de um paciente, ao longo do tempo t. Esses pesquisadores controlam o processo, observando que Q é uma função quadrática de t. Os dados coletados nas duas primeiras horas foram:
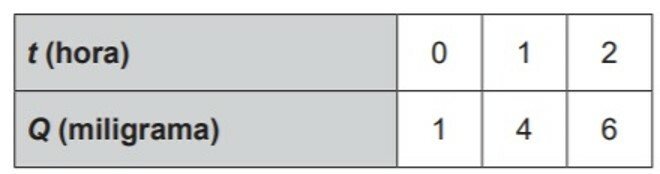
Para decidir se devem interromper o processo, evitando riscos ao paciente, os pesquisadores querem saber, antecipadamente, a quantidade da substância que estará circulando na corrente sanguínea desse paciente após uma hora do último dado coletado.
Nas condições expostas, essa quantidade (em miligrama) será igual a
Objetivo
Determinar a quantidade Q no instante t=3.
A função é do 2º grau
Para determinar os coeficientes a, b e c, substituimos pelos valores da tabela, para cada instante t.
Para t = 0, Q = 1
Para t = 1, Q = 4
Para t = 2, Q = 6
Isolando a na equação I
3 = a + b
a = 3 - b
Substituindo na equação II
5 = 4(3-b) + 2b
5 = 12 - 4b + 2b
5 = 12 -2b
2b = 12 - 5
2b = 7
b = 7/2
Uma vez que b foi determinado, substituimos novamente seu valor.
a = 3 - b
a = 3 - 7/2
a = -1/2
Substituindo os valores de a, b e c na fórmula geral e calculando para t = 3.
a = -1/2
b = 7/2
c = 1
Questão 37
O instrumento de percussão conhecido como triângulo é composto por uma barra fina de aço, dobrada em um formato que se assemelha a um triângulo, com uma abertura e uma haste, conforme ilustra a Figura 1.
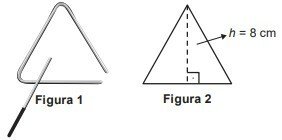
Uma empresa de brindes promocionais contrata uma fundição para a produção de miniaturas de instrumentos desse tipo. A fundição produz, inicialmente, peças com o formato de um triângulo equilátero de altura h, conforme ilustra a Figura 2. Após esse processo, cada peça é aquecida, deformando os cantos, e cortada em um dos vértices, dando origem à miniatura. Assuma que não ocorram perdas de material no processo de produção, de forma que o comprimento da barra utilizada seja igual a o perímetro do triângulo equilátero representado na Figura 2.
Considere 1,7 como valor aproximado para √3.
Nessas condições, o valor que mais se aproxima da medida do comprimento da barra, em centímetro, é
Objetivo
Determinar o comprimento da barra, que é o perímetro do triângulo.
Resolução
O perímetro do triângulo é 3L, pois L + L + L = 3L.
Da figura 2, considerando a metade do triângulo equilátero original, temos um triângulo retângulo.
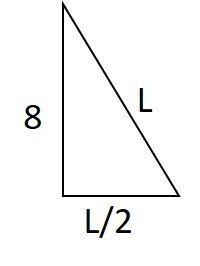
Utilizando o teorema de pitágoras:
Racionalizando para retirar a raíz do denominador:
Como o perímetro é igual a 3L
Questão 38
Devido aos fortes ventos, uma empresa exploradora de petróleo resolveu reforçar a segurança de suas plataformas marítimas, colocando cabos de aço para melhor afixar a torre central.
Considere que os cabos ficarão perfeitamente esticados e terão uma extremidade no ponto médio das arestas laterais da torre central (pirâmide quadrangular regular) e a outra no vértice da base da plataforma (que é um quadrado de lados paralelos aos lados da base da torre central e centro coincidente com o centro da base da pirâmide), como sugere a ilustração.
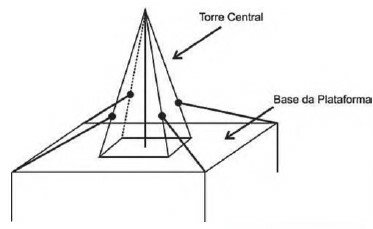
Se a altura e a aresta da base da torre central medem, respectivamente, 24 m e 6√2 m e o lado da base da plataforma mede 19√2 m, então a medida, em metros, de cada cabo será igual a
Objetivo
Determinar o comprimento de cada cabo.
Dados
O cabo está fixo no ponto médio da aresta da pirâmide.
Altura da torre 24 m.
Medida da aresta da base da pirâmide 6√2 m.
Medida da aresta do lado da plataforma 19√2 m.
Resolução
Para determinar o comprimento do cabo determinamos a altura do ponto de fixação em relação à base da pirâmide e a distância da projeção do cabo, até a fixação no vértice da plataforma.
Uma vez que temos às duas medidas, forma-se um triângulo retângulo e, o comprimento do cabo é determinado pelo teorema de Pitágoras.
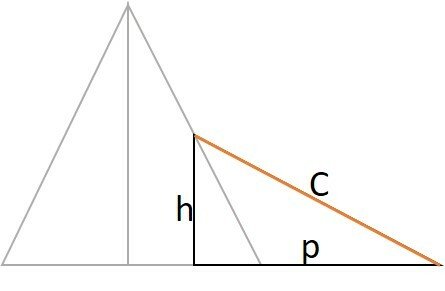
C é o comprimento do cabo (objetivo da questão)
h altura em relação à base da plataforma.
p é a projeção do cabo na base da plataforma.
Passo 1: altura do ponto de fixação em relação à base da plataforma.
Analisando a pirâmide em sua vista lateral podemos determinar a altura em que o cabo está fixo em relação à base da plataforma.
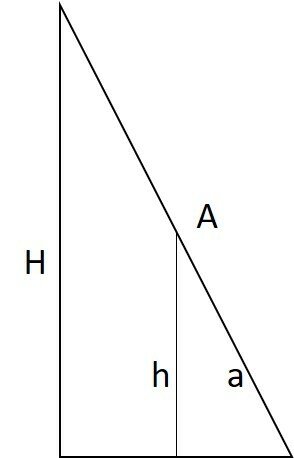
O triângulo menor é semalhante ao maior, visto que seus ângulos são iguais.
Vale a proporção:
Onde,
H é a altura da pirâmide = 24 m.
h é a altura do triângulo menor.
A a aresta da torre.
a é a hipotenusa do triângulo menor.
Como o cabo está no ponto médio de A, a hipotenusa do triângulo menor, é a metade de A.
Substituindo na proporção, temos:
Logo, h = 24/2 = 12 m
Passo 2: projeção p cabo em relação à base da plataforma.
Analisando a vista superior (olhando de cima para baixo), verifica-se que o comprimento p é composto de dois segmentos.
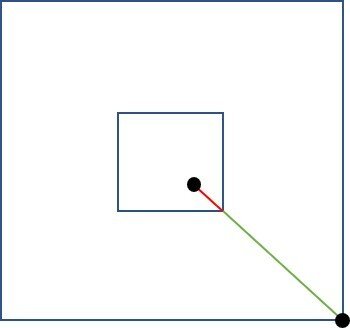
Os pontos pretos representam as fixações do cabo.
Para determinar o seguimento p, começamos calculando a diagonal do quadrado maior, que é a plataforma.
Para isto, utilizamos o teorema de Pitágoras.
Podemos descartar a metade da diagonal.
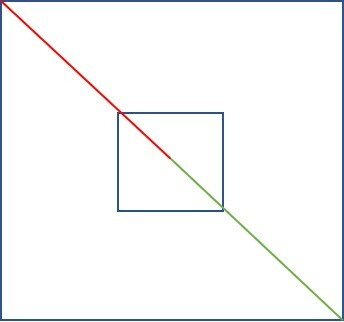
38 / 2 = 19 m
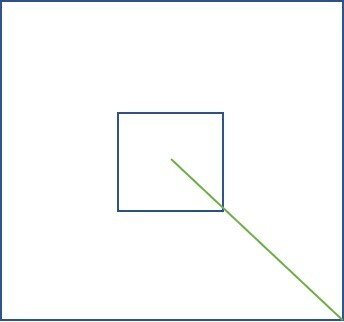
Agora descartamos mais 1/4 da diagonal do quadrado interno, que representa a torre.
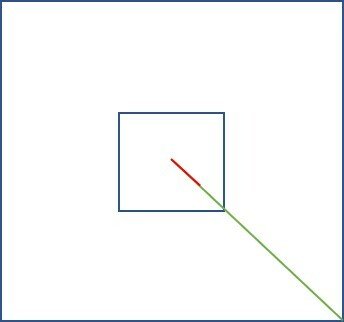
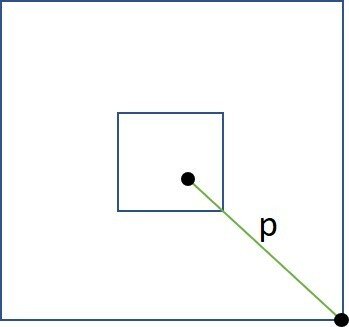
Os pontos destacados na última figura são as extremidades do cabo e p, a projeção do cabo sobre o piso da plataforma.
Para calcular a diagonal do quadrado interno, utilizamos o teorema de Pitágoras.
Logo,
Assim, a medida da projeção é:
Passo 3: cálculo do comprimento do cabo c
Voltando a figura inicial, determinamos p com o uso do teorema de Pitágoras.
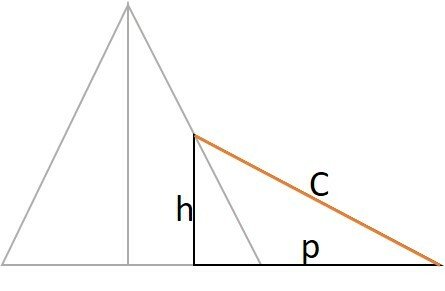
Conclusão
Cada cabo mede m. Esta é a forma como a resposta está apresentada. Também pode-se dizer que cada cabo mede 20 m.
Questão 39
A estimativa do número de indivíduos de uma população de animais frequentemente envolve a captura, a marcação e, então, a liberação de alguns desses indivíduos. Depois de um período, após os indivíduos marcados se misturarem com os não marcados, realiza-se outra amostragem. A proporção de indivíduos desta segunda amostragem que já estava marcada pode ser utilizada para estimar o tamanho da população, aplicando-se a fórmula:
Onde:
n1= número de indivíduos marcados na primeira amostragem;
n2= número de indivíduos marcados na segunda amostragem;
m2= número de indivíduos da segunda amostragem que foram marcados na primeira amostragem;
N= tamanho estimado da população total.
SADAVA, D. et al. Vida: a ciência da biologia. Porto Alegre: Artmed, 2010 (adaptado).
Durante uma contagem de indivíduos de uma população, na primeira amostragem foram marcados 120; na segunda amostragem foram marcados 150, dos quais 100 já possuíam a marcação.
O número estimado de indivíduos dessa população é
Objetivo
Determinar o número de indivíduos N.
Dados
n1 = 120
n2 = 150
m2 = 100
Substituindo na fórmula, temos:
Isolando N
Questão 40
Um casal e seus dois filhos saíram, com um corretor de imóveis, com a intenção de comprar um lote onde futuramente construiriam sua residência. No projeto da casa, que esta família tem em mente, irão necessitar de uma área de pelo menos 400 m². Após algumas avaliações, acaram de decidir entre os lotes 1 e 2 da figura, em forma de paralelogramos, cujos preços são R$ 100 000,00 e R$ 150 000,00, respectivamente.
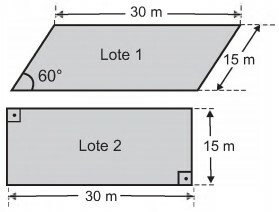
Para colaborarem na decisão, os envolvidos fizeram as seguintes argumentações:
Pai: Devemos comprar o Lote 1, pois como uma de suas diagonais é maior do que as diagonais do Lote 2, o Lote 1 também terá maior área;
Mãe: Se desconsiderarmos os preços, poderemos comprar qualquer lote para executar nosso projeto, pois tendo ambos o mesmo perímetro, terão também a mesma área;
Filho 1: Devemos comprar o Lote 2, pois é o único que tem área suficiente para a execução do projeto;
Filho 2: Devemos comprar o Lote 1, pois como os dois lotes possuem lados de mesma medida, terão também a mesma área, porém o Lote 1 é mais barato;
Corretor: Vocês devem comprar o Lote 2, pois é o que tem menor custo por metro quadrado.
A pessoa que argumentou corretamente para a compra do terreno foi o(a)
O projeto requer pelo menos 400 m².
Cálculo das áreas
Lote 2
Área = 30 x 15 = 450 m²
Lote 1
Temos que a base é 30 m e a altura podemos determinar utilizando o seno de 60º.
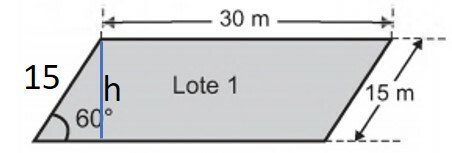
Utilizando o valor de = 1,7, fornecido pela questão:
A área do lote 1 é:
Sobre as argumentações:.
O filho 1 está correto.
Em relação ao corretor, de qualquer forma o lote 1 não satisfaz o projeto. Ainda:
Lote 1
Lote 2
O lote 2 tem o maior custo por metro quadrado.
Pai: ERRADO. A área não é determinada pela diagonal.
Mãe: ERRADA. A área não é determinada pelo perímetro.
Filho 2: ERRADO. A área não é determinada considerando apenas a medida dos lados em formas diferentes.
Questão 41
Considere que um professor de arqueologia tenha obtido recursos para visitar 5 museus, sendo 3 deles no Brasil e 2 fora do país. Ele decidiu restringir sua escolha aos museus nacionais e internacionais relacionados na tabela a seguir.
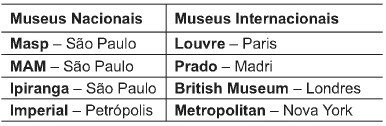
De acordo com os recursos obtidos, de quantas maneiras diferentes esse professor pode escolher os 5 museus para visitar?
Há quatro nacionais e quatro internacionais.
Serão visitados cindo ao total, sendo 3 nacionais e 2 internacionais.
De quantos modos pode-se escolher 3 opções entre 4 e, 2 opções entre 4.
Pelo princípio fundamental da contagem:
3 opções entre 4 . 2 opções entre 4
Trata-se de uma combinação para os nacionais e para os internacionais.
Para os museus nacionais:
Para os museus internacionais:
Fazendo o produto, temos:
6 . 4 = 24 opções
Questão 42
Um confeiteiro deseja fazer um bolo cuja receita indica a utilização de açúcar e farinha de trigo em quantidades fornecidas em gramas. Ele sabe que uma determinada xícara utilizada para medir os ingredientes comporta 120 gramas de farinha de trigo e que três dessas xícaras de açúcar correspondem, em gramas, a quatro de farinha de trigo.
Quantos gramas de açúcar cabem em uma dessas xícaras?
1 xícara de trigo = 120g
3 xícaras de açucar = 4 xícaras de trigo
3 xícaras de açucar = 4 . 120
3 xícaras de açucar = 480
Logo, 1 xícara de açucar = 480 / 3 = 160g
Questão 43
Os sistemas de cobrança dos serviços de táxi nas cidades A e B são distintos. Uma corrida de táxi na cidade A é calculada pelo valor fixo da bandeirada, que é de R$ 3,45, mais R$ 2,05 por quilômetro rodado. Na cidade B, a corrida é calculada pelo valor fixo da bandeirada, que é de R$ 3,60, mais R$ 1,90 por quilômetro rodado.
Uma pessoa utilizou o serviço de táxi nas duas cidades para percorrer a mesma distância de 6 km.
Qual o valor que mais se aproxima da diferença, em reais, entre as médias do custo por quilômetro rodado ao final das duas corridas?
Dados
6 km rodados nas duas cidades.
Custo total na cidade A
A = 3,45 + 2,05 . 6 = 15,75
Custo por km na cidade A (média por km)
15,75 / 6 = 2,625
Custo total na cidade B
B = 3,60 + 1,90 . 6 = 15
Custo por km na cidade B (média por km)
15 / 6 = 2,5
Diferença entre as médias
2,625 - 2,5 = 0,125
A resposta mais próxima é a letra e) 0,13.
Questão 44
Num campeonato de futebol de 2012, um time sagrou-se campeão com um total de 77 pontos (P) em 38 jogos, tendo 22 vitórias (V), 11 empates (E) e 5 derrotas (D). No critério adotado para esse ano, somente as vitórias e empates têm pontuações positivas e inteiras. As derrotas têm valor zero e o valor de cada vitória é maior que o valor de cada empate.
Um torcedor, considerando a fórmula da soma de pontos injusta, propôs aos organizadores do campeonato que, para o ano de 2013, o time derrotado em cada partida perca 2 pontos, privilegiando os times que perdem menos ao longo do campeonato. Cada vitória e cada empate continuariam com a mesma pontuação de 2012.
Qual a expressão que fornece a quantidade de pontos (P), em função do número de vitórias (V), do número de empates (E) e do número de derrotas (D), no sistema de pontuação proposto pelo torcedor para o ano de 2013?
Objetivo
Determinar a quantidade de pontos P em função do número de vitórias V, derrotas D e empates E, segundo o critério sugerido pelo torcedor.
Dados
Inicialmente:
- Vitórias e empates resultam positivo.
- Vitória vale mais que empate.
- Derrotas valem 0.
Sugestão do torcedor
- Derrota perde 2 pontos e vitória e empate continuam iguais.
Resolução
Inicialmente a função deve ser:
P = xV + yE - 2D
O termo -2D se refere a perda de 2 pontos a cada derrota.
Falta identificarmos os coeficientes: x para as vitórias e y, para os empates.
Por eliminação, restam apenas as opções b) e d).
Como na opção b) o termo E não aparece, significa que seu coeficiente é zero 0. Mas a regra diz que devem ser positivos, portanto, diferente de zero.
Desta forma, resta apenas a opção d) P = 3V + E - 2D.
Questão 45
Um laboratório realizou um teste para calcular a velocidade de reprodução de um tipo de bactéria. Para tanto, realizou um experimento para observar a reprodução de uma quantidade x dessas bactérias por um período de duas horas. Após esse período, constava no habitáculo do experimento uma população de 189 440 da citada bactéria. Constatou-se, assim, que a população de bactérias dobrava a cada 0,25 hora.
A quantidade inicial de bactérias era de
Objetivo
Determinar a quantidade inicial x.
Dados
Evolução durante duas horas.
Dobra a cada 0,25h
População final = 189 440
Resolução
0,25h = 15 min
2h = 120 min
120/15 = 8
Isto significa que a população dobra oito vezes.
Início x
1ª dobra: 2x
2ª dobra: 4x
3ª dobra: 8x
4ª dobra: 16x
5ª dobra: 32x
6ª dobra: 64x
7ª dobra: 128x
8ª dobra: 256x
256x = 189 440
x = 189 440/256
x = 740
Referências Bibliográficas
Inep - Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira
https://www.gov.br/inep/pt-br/areas-de-atuacao/avaliacao-e-exames-educacionais/enem
ASTH, Rafael. Simulado de Matemática e suas Tecnologias (ENEM). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/simulado-enem-de-matematica/. Acesso em:


