Soma dos ângulos internos de um polígono

Rafael C. Asth

Professor de Matemática e Física

A soma dos ângulos internos de um polígono convexo pode ser determinada conhecendo o número de lados (n), bastando subtrair este valor por dois (n - 2) e multiplicar por 180°.

Um polígono é uma superfície fechada formada por uma linha poligonal, ou seja, os lados são segmentos de reta, e o encontro entre dois lados forma um ângulo. No caso do polígono ser convexo, todos os ângulos internos são menores que 180°.

Soma dos ângulos internos de um polígono convexo

Para somar os ângulos internos de um polígono convexo ou conhecemos os valores de todos os ângulos e somamos, ou podemos determinar a soma conhecendo o número de lados deste polígono.

Conhecer o total de lados de um polígono é, em muitos casos, uma informação mais fácil de obter do que os valores de cada ângulo.

Fórmula da soma dos ângulos internos de um polígono

Para determinar a soma dos ângulos internos de um polígono convexo conhecendo apenas o número de lados, utilizamos a fórmula:

$começar estilo tamanho matemático 18px reto S com reto i subscrito igual a 180 sinal de grau sinal de multiplicação parêntese esquerdo reto n menos 2 parêntese direito fim do estilo$

Onde,
Si é a soma, o total de graus de todos os ângulos.
n é o número de lados.

Exemplo
A soma dos ângulos internos de um quadrilátero é:

Como um quadrilátero possui 4 lados, n será igual a 4.

$começar estilo tamanho matemático 14px reto S com reto i subscrito igual a 180 sinal de grau espaço sinal de multiplicação espaço parêntese esquerdo reto n menos 2 parêntese direito reto S com reto i subscrito igual a 180 sinal de grau espaço sinal de multiplicação espaço parêntese esquerdo 4 menos 2 parêntese direito reto S com reto i subscrito igual a 180 sinal de grau espaço sinal de multiplicação espaço 2 reto S com reto i subscrito igual a 360 sinal de grau fim do estilo$

Soma dos ângulos internos de um polígono regular

A soma dos ângulos internos de um polígono regular é calculada da mesma forma. Um polígono é regular quando possui todos os lados e ângulos com medidas iguais. O número de ângulos é sempre igual o número de lados.

Ângulo interno de um polígono regular

Como todos os ângulos possuem mesma medida, basta dividir a soma dos ângulos internos pelo número de ângulos, portanto, número de lados.

$reto a com reto i subscrito igual a reto S com reto i subscrito sobre reto n$

Onde,
Si é a soma, o total de graus de todos os ângulos.
n é o número de lados.

Exemplo
A medida dos ângulos internos de um pentágono regular é:

Primeiro determinamos a soma de seus ângulos internos usando n = 5.

$Error converting from MathML to accessible text.$

Agora, basta dividir pelo número de lados.

$reto a com reto i subscrito igual a reto S com reto i subscrito sobre reto n igual a numerador 540 sinal de grau sobre denominador 5 fim da fração igual a 108 sinal de grau$

Nome de polígonos em função dos lados

Nome de alguns polígonos em função da quantidade de lados.

Nº de lados	Nome
3	Triângulo
4	Quadrilátero
5	Pentágono
6	Hexágono
7	Heptágono
8	Octógono
9	Eneágono
10	Decágono
11	Undecágono
12	Dodecágono
20	Icoságono

Dedução da fórmula da soma dos ângulos internos de um polígono

Partimos da premissa de que todo triângulo possui 180° como soma de seus ângulos internos.

A partir de um vértice qualquer de um polígono convexo, podemos traçar diagonais e formar triângulos.

Dedução da fórmula — Polígono dividido em quatro triângulos.

Como a soma dos ângulos internos de cada triângulo é igual a 180°, basta multiplicar o número de triângulos formados por 180°.

$reto S com reto i subscrito igual a 180 sinal de grau espaço sinal de multiplicação espaço reto n º espaço de espaço triângulos.$

Podemos observar que a quantidade de triângulos formados é sempre igual ao número de lados menos 2.

Para um triângulo, n =3.
$parêntese esquerdo n menos 2 parêntese direito espaço igual a espaço parêntese esquerdo 3 menos 2 parêntese direito espaço igual a espaço 1$

Para um quadrilátero, n = 4.

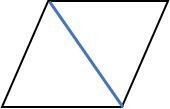
Há 2 triângulos:
$parêntese esquerdo n menos 2 parêntese direito espaço igual a espaço parêntese esquerdo 4 menos 2 parêntese direito igual a espaço 2$

Para um pentágono, n = 5.

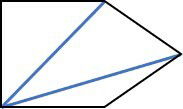
Há 3 triângulos:
$parêntese esquerdo n menos 2 parêntese direito espaço igual a espaço parêntese esquerdo 5 menos 2 parêntese direito espaço igual a espaço 3$

Desta forma, podemos generalizar e substituir o termo nº de triângulos por (n-2) e a fórmula fica assim:

$Error converting from MathML to accessible text.$

Aprenda mais sobre polígonos e ângulos.

Exercícios

Exercício 1

Determine a soma dos ângulos internos de um polígono convexo com 17 lados.

Ver Resposta

Resposta: 2 700º

$começar estilo tamanho matemático 16px reto S com reto i subscrito igual a 180 sinal de grau sinal de multiplicação parêntese esquerdo reto n menos 2 parêntese direito reto S com reto i subscrito igual a 180 sinal de grau sinal de multiplicação parêntese esquerdo 17 menos 2 parêntese direito reto S com reto i subscrito igual a 180 sinal de grau sinal de multiplicação espaço 15 reto S com reto i subscrito igual a 2 espaço 700 sinal de grau fim do estilo$

Exercício 2

Qual o nome de um polígono cuja soma dos ângulos internos é igual a 1 440°?

Ver Resposta

Resposta: O polígono cuja soma dos ângulos internos é 1 440° se chama decágono, e possui 10 lados.

$reto S com reto i subscrito igual a 180 sinal de grau sinal de multiplicação parêntese esquerdo reto n menos 2 parêntese direito 1 espaço 440 sinal de grau igual a 180 sinal de grau sinal de multiplicação espaço parêntese esquerdo reto n menos 2 parêntese direito numerador 1 espaço 440 sinal de grau sobre denominador 180 sinal de grau fim da fração igual a reto n menos 2 8 espaço igual a espaço reto n espaço menos espaço 2 8 espaço mais espaço 2 espaço igual a espaço reto n 10 espaço igual a espaço reto n$

Exercício 3

Determine o valor dos ângulos internos de um octógono regular.

Ver Resposta

Resposta: Em octógono regular, cada ângulo interno mede 135º.

Primeiro devemos determinar a soma dos ângulos internos de um octógono. Como possui oito lados, n = 8.

$reto S com reto i subscrito igual a 180 sinal de grau sinal de multiplicação parêntese esquerdo reto n menos 2 parêntese direito reto S com reto i subscrito igual a 180 sinal de grau sinal de multiplicação parêntese esquerdo 8 menos 2 parêntese direito reto S com reto i subscrito igual a 180 sinal de grau sinal de multiplicação espaço 6 reto S com reto i subscrito igual a 1 espaço 080 sinal de grau$

Como o polígono é regular, todos os ângulos internos possuem a mesma medida e, basta dividir o total por 8.

$reto a com reto i subscrito igual a reto S com reto i subscrito sobre reto n igual a numerador 1 espaço 080 sobre denominador 8 fim da fração igual a 135 sinal de grau$

Pratique mais exercícios sobre polígonos.

Veja também:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.