Soma dos ângulos internos de um triângulo

Rafael C. Asth

Professor de Matemática e Física

Uma das propriedades mais importantes dos triângulos é que a soma de seus ângulos internos é sempre igual a 180º. Essa propriedade é válida para qualquer triângulo, seja ele acutângulo, retângulo ou obtusângulo.

Os ângulos internos de um triângulo são os ângulos formados entre seus lados, no interior figura. Em qualquer triângulo, existem três ângulos internos.

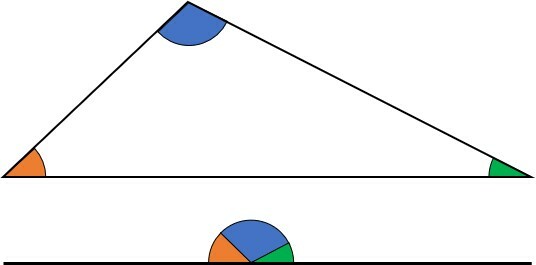
Soma dos ângulos de um triângulo — Os três ângulos juntos formam meio volta (180º)

Independente da configuração do triângulo e de quais sejam os valores de cada um de seus três ângulos internos, ao somá-los, o resultado será 180º. Esta propriedade é útil em situações em que um ângulo é desconhecido, podendo ser obtido facilmente. .

Exemplos de uso da propriedade da soma = 180º

Exemplo 1
Dado o triângulo da imagem, determine o valor em graus do ângulo desconhecido.

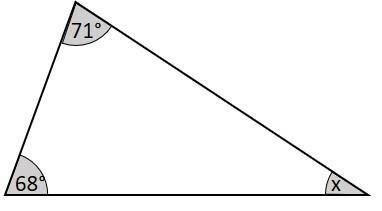
Resolução:

Pata determinar o valor do ângulo desconhecido x, utilizamos a propriedade da soma dos ângulos internos de um triângulo.

$71 espaço mais espaço 68 espaço mais espaço reto x espaço igual a espaço 180 reto x espaço igual a espaço 180 espaço menos espaço 71 espaço menos espaço 68 reto x espaço igual a 41$

Logo, a medida x do ângulo desconhecido é de 41º.

Exemplo 2
No triângulo isósceles a seguir, determine o valor em graus dos ângulos da base.

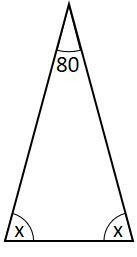
Resolução:

Em um triângulo isósceles, os ângulos da base são iguais. Nomeemos cada um como x. Como há dois iguais, somando os ângulos internos do triângulo, temos:

$reto x espaço mais espaço reto x espaço mais espaço 80 espaço igual a espaço 180 2 reto x espaço igual a espaço 180 espaço menos espaço 80 2 reto x espaço igual a espaço 100 reto x espaço igual a espaço 100 sobre 2 reto x espaço igual a espaço 50$

Assim, cada ângulo da base do triângulo possui 180º.

Exemplo 3
Determine o valor de cada ângulo no triângulo da imagem.

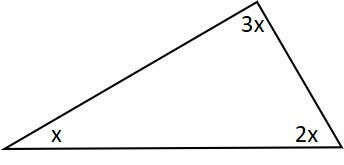
Resolução:

Somando os ângulos internos e igualando a 180º:

$reto x espaço mais espaço 2 reto x espaço mais espaço 3 reto x igual a 180 6 reto x igual a 180 reto x igual a 180 sobre 6 reto x igual a 30$

Temos que cada x é igual a 30º. Multiplicando, é possível determinar a medida de cada ângulo.

x = 30
2x = 2 . 30 = 60
3x = 3 . 30 = 90

Deste forma, os três ângulos internos do triângulo são: 30º, 60º e 90º.

Demonstração da soma igual a 180º

Para demostrar a propriedade da soma dos ângulos internos igual a 180º, utilizamos um triângulo ABC qualquer. Também traçamos sobre o vértice A, uma linha paralela ao lado BC.

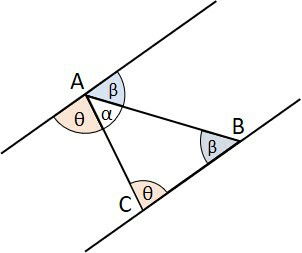
Os ângulos beta e teta formam ângulos alternos internos com a reta paralela que foi traçada, o que significa que eles são iguais aos ângulos formados pela reta no vértice A.

Fica fácil identificar que a união dos três ângulos forma o ângulo de meia volta ou, 180º.

Aprenda mais sobre os triângulos em:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações