Trigonometria no Triângulo Retângulo
A trigonometria no triângulo retângulo é o estudo sobre os triângulos que possuem um ângulo interno de 90°, chamado de ângulo reto.
Lembre-se que a trigonometria é a ciência responsável pelas relações estabelecidas entre os triângulos. Eles são figuras geométricas planas compostas de três lados e três ângulos internos.
O triângulo chamado equilátero possui os lados com medidas iguais. O isósceles possui dois lados com medidas iguais. Já o escaleno tem os três lados com medidas diferentes.
No tocante aos ângulos dos triângulos, os ângulos internos maiores que 90° são chamados de obtusângulos. Já os ângulos internos menores que 90° são denominados de acutângulos.
Além disso, a soma dos ângulos internos de um triângulo será sempre 180°.
Composição do Triângulo Retângulo
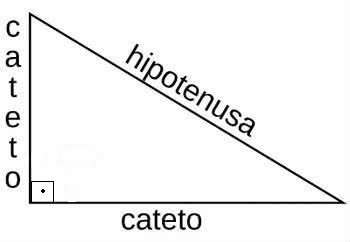
O triângulo retângulo é formado:
- Catetos: são os lados do triângulo que formam o ângulo reto. São classificados em: cateto adjacente e cateto oposto.
- Hipotenusa: é o lado oposto ao ângulo reto, sendo considerado o maior lado do triângulo retângulo.
Segundo o Teorema de Pitágoras, a soma dos quadrado dos catetos de um triângulo retângulo é igual ao quadrado de sua hipotenusa:
h2 = ca2 + co2
Leia também:
Relações Trigonométricas do Triângulo Retângulo
As razões trigonométricas são as relações existentes entre os lados de um triângulo retângulo. As principais são o seno, o cosseno e a tangente.
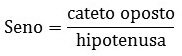
Lê-se cateto oposto sobre a hipotenusa.
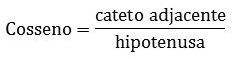
Lê-se cateto adjacente sobre a hipotenusa.
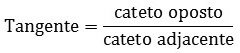
Lê-se cateto oposto sobre o cateto adjacente.
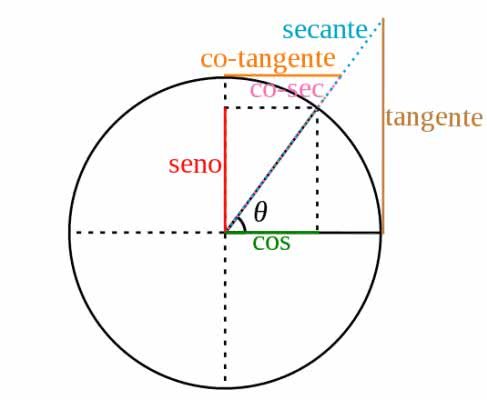
Círculo trigonométrico e as razões trigonométricas
O círculo trigonométrico é utilizado para auxiliar nas relações trigonométricas. Acima, podemos encontrar as principais razões, sendo que o eixo vertical corresponde ao seno e o eixo horizontal ao cosseno. Além delas, temos as razões inversas: secante, cossecante e cotangente.
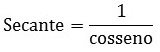
Lê-se um sobre o cosseno.
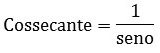
Lê-se um sobre o seno.
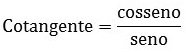
Lê-se cosseno sobre o seno.
Leia também:
- Seno, Cosseno e Tangente
- Círculo Trigonométrico
- Funções Trigonométricas
- Razões Trigonométricas
- Relações Métricas no Triângulo Retângulo
- Identidades trigonométricas
- Exercícios sobre razões trigonométricas
Ângulos Notáveis
Os chamados ângulos notáveis são aqueles que aparecem com mais frequência, a saber:
| Relações Trigonométricas | 30° | 45° | 60° |
|---|---|---|---|
| Seno | 1/2 | √2/2 | √3/2 |
| Cosseno | √3/2 | √2/2 | 1/2 |
| Tangente | √3/3 | 1 | √3 |
Saiba mais:
- Exercícios de Trigonometria no triângulo retângulo
- Exercícios de Trigonometria
- Lei dos Senos
- Lei dos Cossenos
- Relações Trigonométricas
- Tabela Trigonométrica
- Exercícios sobre funções trigonométricas com respostas
Exercício Resolvido
Num triângulo retângulo a hipotenusa mede 8 cm e um dos ângulos internos possui 30°. Qual o valor dos catetos oposto (x) e adjacente (y) desse triângulo?
De acordo com as relações trigonométricas, o seno é representado pela seguinte relação:
Sen = cateto oposto/hipotenusa
Sen 30° = x/8
½ = x/8
2x = 8
x = 8/2
x = 4
Logo, o cateto oposto desse triângulo retângulo mede 4 cm.
A partir disso, se o quadrado da hipotenusa é a soma dos quadrados de seus catetos, temos:
Hipotenusa2 = Cateto oposto2 + Cateto adjacente2
82 = 42+y2
82 - 42 = y2
64 - 16 = y2
y2 = 48
y = √48
Logo, o cateto adjacente desse triângulo retângulo mede √48 cm.
Assim, podemos concluir que os lados desse triângulo medem 8 cm, 4 cm e √48 cm. Já seus ângulos internos são de 30° (acutângulo), 90° (reto) e 60° (acutângulo), visto que a soma dos ângulos internos dos triângulos sempre será 180°.
Veja também:
Exercícios de Vestibular
1. (Vunesp) O cosseno do menor ângulo interno de um triângulo retângulo é √3/2. Se a medida da hipotenusa desse triângulo é 4 unidades, então é verdade que um dos catetos desse triângulo mede, na mesma unidade,
a) 1
b) √3
c) 2
d) 3
e) √3/3
2. (FGV) Na figura a seguir, o segmento BD é perpendicular ao segmento AC.
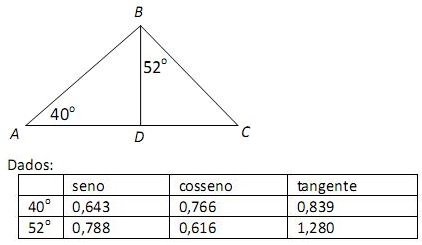
Se AB = 100m, um valor aproximado para o segmento DC é:
a) 76m.
b) 62m.
c) 68m.
d) 82m.
e) 90m.
3. (FGV) A plateia de um teatro, vista de cima para baixo, ocupa o retângulo ABCD da figura a seguir, e o palco é adjacente ao lado BC. As medidas do retângulo são AB = 15m e BC = 20m.
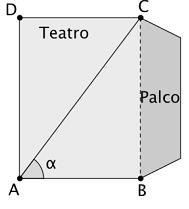
Um fotógrafo que ficará no canto A da plateia deseja fotografar o palco inteiro e, para isso, deve conhecer o ângulo da figura para escolher a lente de abertura adequada.
O cosseno do ângulo da figura acima é:
a) 0,5
b) 0,6
c) 0,75
d) 0,8
e) 1,33
4. (Unoesc) Um homem de 1,80 m encontra-se a 2,5 m de distância de uma árvore, conforme ilustração a seguir. Sabendo-se que o ângulo α é de 42°, determine a altura dessa árvore.
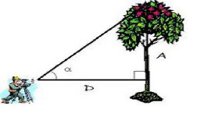
Use:
Seno 42° = 0,669
Cosseno 42° = 0,743
Tangente de 42° = 0,90
a) 2,50 m.
b) 3,47 m.
c) 3,65 m.
d) 4,05 m.
5. (Enem-2013) As torres Puerta de Europa são duas torres inclinadas uma contra a outra, construídas numa avenida de Madri, na Espanha. A inclinação das torres é de 15° com a vertical e elas têm, cada uma, uma altura de 114 m (a altura é indicada na figura como o segmento AB). Estas torres são um bom exemplo de um prisma oblíquo de base quadrada e uma delas pode ser observada na imagem.

Disponível em: www.flickr.com. Acesso em: 27 mar. 2012.
Utilizando 0,26 como valor aproximado para a tangente de 15° e duas casas decimais nas operações, descobre-se que a área da base desse prédio ocupa na avenida um espaço:
a) menor que 100m2.
b) entre 100 m2 e 300 m2.
c) entre 300 m2 e 500 m2.
d) entre 500 m2 e 700 m2.
e) maior que 700 m2.
GOUVEIA, Rosimar. Trigonometria no Triângulo Retângulo. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/trigonometria-no-triangulo-retangulo/. Acesso em:


