Acelere seu aprendizado

Volume da Esfera: fórmula, exemplo e exercícios

Rafael C. Asth

Professor de Matemática e Física

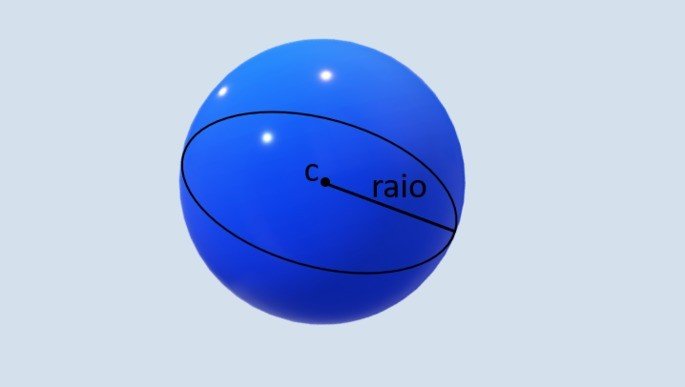
O volume de uma esfera é calculado com base no comprimento do seu raio, que corresponde à distância entre o centro da esfera e qualquer ponto de sua superfície.

A esfera é um sólido geométrico tridimensional formado por todos os pontos do espaço que estão a uma distância igual ou menor que o raio, em relação ao seu centro.

Esfera de raio r

Fórmula do volume da esfera

$começar estilo tamanho matemático 20px reto V espaço igual a espaço numerador 4. reto pi. espaço reto r ao cubo sobre denominador 3 fim da fração fim do estilo$

Onde:

V é o volume da esfera (m³);
r é raio (m);
π (Pi) é, aproximadamente, 3,1415. Sendo um número irracional, possui infinitas casas não periódicas.

Exemplo:
Um reservatório esférico possui um raio interno de 2 m. Qual a capacidade deste reservatório?
Utilize π = 3,14.

Resolução:

$V igual a espaço numerador 4. pi. espaço r ao cubo sobre denominador 3 fim da fração espaço V igual a espaço numerador 4. pi. espaço 2 ao cubo sobre denominador 3 fim da fração espaço V espaço igual a numerador 4. pi espaço. espaço 2 espaço. espaço 2 espaço. espaço 2 sobre denominador 3 fim da fração V espaço igual a numerador 4 espaço. espaço 3 vírgula 14 espaço. espaço 2 espaço. espaço 2 espaço. espaço 2 sobre denominador 3 fim da fração V espaço igual a numerador 100 vírgula 48 sobre denominador 3 fim da fração igual a 33 vírgula 49333 espaço... V espaço aproximadamente igual espaço 33 vírgula 50 espaço m ao cubo espaço$

Exercícios sobre volume da esfera

Exercício 1

(VUNESP) Considere uma pulseira formada por 22 esferas de hematita (Fe2O3 ), cada esfera com raio igual a 0,5 cm.

Remover anúncios

O fecho e o fio que unem as esferas dessa pulseira têm massas e volumes desprezíveis e a densidade da hematita é cerca de 5,0 g/cm³. Sabendo que o volume de uma esfera é calculado pela expressão 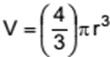, a massa, em gramas, dessa pulseira é próxima de

a) 110.
b) 82.
c) 58.
d) 136.
e) 150.

Ver Resposta

Resposta correta: c) 58.

Resolução

Dados
22 esferas
raio (r) = 0,5 cm
Densidade (d) = 5,0 g/cm³

Objetivo
Determinar a massa da pulseira, em gramas.

Passo 1: determinar o volume de todas as esferas do colar.

Volume de 1 esfera

$V espaço igual a espaço numerador 4 espaço. espaço pi espaço. espaço r ao cubo sobre denominador 3 fim da fração V espaço igual a numerador 4 espaço. espaço pi espaço. espaço 0 vírgula 5 ao cubo espaço sobre denominador 3 fim da fração V espaço igual a espaço numerador 4 espaço. espaço pi espaço. espaço 0 vírgula 125 sobre denominador 3 fim da fração V espaço igual a numerador 0 vírgula 5 espaço pi sobre denominador 3 fim da fração$

Volume das 22 esferas

$V com p u l s e i r a subscrito fim do subscrito espaço igual a espaço 22 espaço sinal de multiplicação espaço numerador 0 vírgula 5 pi sobre denominador 3 fim da fração espaço igual a espaço numerador 11 pi sobre denominador 3 fim da fração espaço c m ao cubo$

Passo 2: relacionar o volume da pulseira com a densidade.

A densidade é a relação entre a massa e o volume.

$d espaço igual a m sobre V$

Isolando a massa m, temos:

$d espaço. espaço V espaço igual a espaço m$

Passo 3: substituir os valores e calcular a massa.

$m espaço igual a espaço 5 vírgula 0 espaço numerador g sobre denominador riscado diagonal para cima sobre c m ao cubo fim do riscado fim da fração espaço sinal de multiplicação espaço numerador 11 pi sobre denominador 3 fim da fração espaço riscado diagonal para cima sobre c m ao cubo fim do riscado m espaço igual a numerador 55 pi sobre denominador 3 fim da fração espaço g$

Aproximando o valor de $reto pi$ para 3:

$m espaço igual a espaço numerador 55 espaço. espaço 3 sobre denominador 3 fim da fração espaço aproximadamente igual espaço 55 espaço g$

Conclusão
Das opções sugeridas, a alternativa c é a que mais se aproxima.

Observação
Se fizermos uma melhor aproximação para $reto pi espaço igual a espaço 3 vírgula 14$ , a massa será cerca de 57,57 g, se aproximando ainda mais da opção c = 58 g.

No entanto, mesmo fazendo $reto pi igual a 3$ , frente as outras opções, foi possível determinar a questão.

Remover anúncios

Exercício 2

(Prefeitura de São Leopoldo — RS 2016) Considerando que uma esfera amarela tenha o raio medindo 10 cm e uma esfera azul, 1 cm, pode-se afirmar que o volume da esfera amarela é ______ vezes maior que o volume da esfera azul. Utilize o valor de π = 3,14.

Assinale a alternativa que preenche corretamente a lacuna do trecho acima.

a) 2
b) 5
c) 10
d) 100
e) 1.000

Ver Resposta

Resposta correta: e) 1 000.

Resolução

Dados
Raio da esfera amarela 10 cm
Raio da esfera azul 1 cm
π = 3,14

Objetivo
Determinar quantas vezes maior a esfera amarela é em relação a azul.

Fórmula do volume da esfera

$V espaço igual a numerador 4 espaço. pi espaço. espaço r ao cubo sobre denominador 3 fim da fração$

Na fórmula do volume, o raio é o único parâmetro variável, o 4, o π e, o 3, são constantes.

Para resolver a comparação, vamos dividir o raio ao cubo da esfera amarela, pelo raio ao cubo da esfera azul, e descartar os outros parâmetros.

$r com a m a r e l a subscrito fim do subscrito ao cubo sobre r com a z u l ao cubo subscrito fim do subscrito igual a 10 ao cubo sobre 1 ao cubo igual a numerador 1 espaço 000 sobre denominador 1 fim da fração igual a 1 espaço 000$

Conclusão
O volume da esfera amarela é 1 000 vezes maior que o volume da esfera azul.

Remover anúncios

Exercício 3

(UECE 2013) Um círculo de raio R gira em torno de seu diâmetro, gerando uma esfera de volume V. Se o raio do círculo é aumentado em 50%, então o volume da esfera é aumentado em:

a) 100,0 %.
b) 125,0 %.
c) 215,0 %.
d) 237,5 %.

Ver Resposta

Resposta correta: d) 237,5%

Considerando o volume inicial, com raio R, igual a 100%

O raio foi aumentando em 50% ou seja, 50% + 100% = 150%. Por isso, basta multiplicar R por 1,5 pois:

$150 sinal de percentagem igual a 150 sobre 100 igual a 1 vírgula 5$

Desta forma, o raio aumentado é:

$1 vírgula 5 espaço R espaço$

Fazendo a comparação entre o volume final e inicial, temos:

$V com f subscrito sobre V com i subscrito igual a numerador começar estilo mostrar numerador 4 espaço pi espaço parêntese esquerdo 1 vírgula 5 espaço R parêntese direito ao cubo sobre denominador 3 fim da fração fim do estilo sobre denominador começar estilo mostrar numerador 4 espaço pi espaço espaço R ao cubo sobre denominador 3 fim da fração fim do estilo fim da fração igual a numerador começar estilo mostrar numerador riscado diagonal para cima sobre 4 espaço pi fim do riscado espaço parêntese esquerdo 1 vírgula 5 espaço R parêntese direito ao cubo sobre denominador diagonal para cima risco 3 fim da fração fim do estilo sobre denominador começar estilo mostrar numerador riscado diagonal para cima sobre 4 espaço pi fim do riscado espaço espaço R ao cubo sobre denominador diagonal para cima risco 3 fim da fração fim do estilo fim da fração igual a numerador 3 vírgula 375 espaço R ao cubo sobre denominador R ao cubo fim da fração igual a 3 vírgula 375$

Para escrever em porcentagem, multiplica-se por 100.

$3 vírgula 375 espaço sinal de multiplicação 100 espaço igual a espaço 337 vírgula 5 sinal de percentagem$

Como o volume inicial era 100% e o volume final 337,5% o volume foi aumentado em:

337,5% - 100% = 237,5%

Para praticar mais: Exercícios sobre volume da esfera (com gabarito resolvido)

Veja também:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações

Remover anúncios