Volume do Cilindro: fórmula e exercícios

O volume do cilindro está relacionado com a capacidade dessa figura geométrica. Lembre-se que o cilindro ou cilindro circular é um sólido geométrico alongado e arredondado.

Ele possui o mesmo diâmetro ao longo de todo o comprimento e duas bases: superior e inferior. As bases são dois círculos paralelos com raios de medidas iguais.

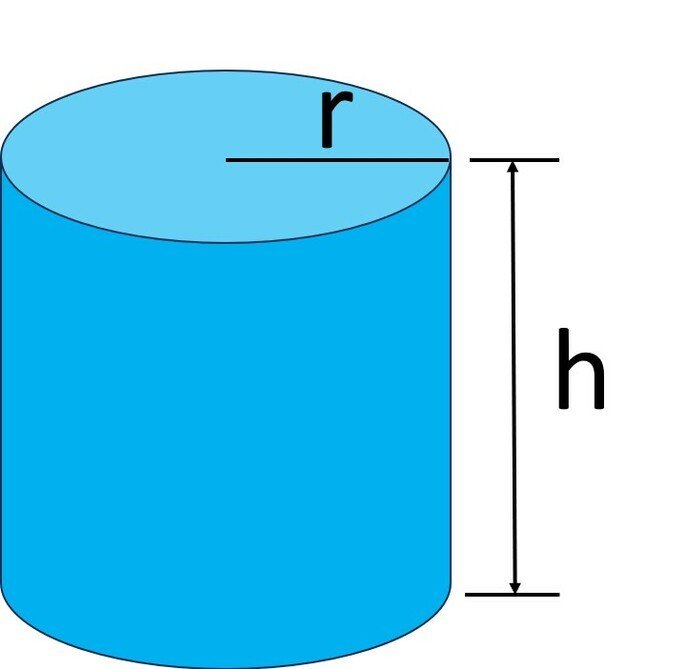
O raio do cilindro é a distância entre o centro da figura e a extremidade. Sendo assim, o diâmetro equivale duas vezes o raio (d=2r).

Muitas figuras de formato cilíndrico estão presentes no nosso cotidiano, por exemplo: pilhas, copos, latas de refrigerante, de achocolatados, de ervilhas, de milho, etc.

Importante notar que o prisma e o cilindro são sólidos geométricos semelhantes, sendo que o volume deles é calculado pela mesma fórmula.

Fórmula do volume do cilindro

A fórmula para encontrar o volume do cilindro corresponde ao produto da área de sua base pela medida da altura.

O volume do cilindro é calculado em cm³ ou m³:

ou

Onde:

V: volume
A_b: área da base
π (Pi): 3,14 (aproximadamente)
r: raio
h: altura

Quer saber mais sobre o tema? Leia os artigos:

• Cilindro
• Área do Cilindro
• Geometria Espacial
• Número Pi
• Volume do Cone
• Volume do Prisma: fórmula e exercícios
• Volume do Cubo

Exemplo 1
Calcule o volume de um cilindro cuja altura mede 10 cm e o diâmetro da base mede 6,2 cm. Utilize o valor de 3,14 para π.

Resolução

Primeiramente, vamos encontrar o valor do raio dessa figura. Lembre-se que o raio é duas vezes o diâmetro. Para tanto, dividimos o valor do diâmetro por 2:

6,2 : 2 = 3,1

Logo,

r: 3,1 cm
h: 10 cm

V = π.r².h
V = π . (3,1)² . 10
V = π . 9,61 . 10
V = π. 96,1
V = 3,14 . 96,1
V = 301,7 cm³

Exemplo 2
Um tambor cilíndrico tem uma base de 60 cm de diâmetro e a altura de 100 cm. Calcule a capacidade desse tambor. Utilize o valor de 3,14 para o π.

Resolução

Primeiramente, vamos encontrar o raio dessa figura, dividindo o valor do diâmetro por 2:

60 : 2 = 30 cm

Assim, basta colocar na fórmula os valores:

V = π.r².h
V = π . (30)² . 100
V = π . 900 . 100
V = 90.000 π
V = 282.600 cm³

Exercícios de volume do cilindro

Exercício 1

A figura abaixo mostra um reservatório de água na forma de cilindro circular reto, com 6 m de altura. Quando está completamente cheio, o reservatório é suficiente para abastecer, por um dia, 900 casas cujo consumo médio diário é de 500 litros de água. Suponha que, um certo dia, após uma campanha de conscientização do uso da água, os moradores das 900 casas abastecidas por esse reservatório tenham feito economia de 10% no consumo de água. Nessa situação:

a) a quantidade de água economizada foi de 4,5 m³.
b) a altura do nível da água que sobrou no reservatório, no final do dia, foi igual a 60 cm.
c) a quantidade de água economizada seria suficiente para abastecer, no máximo, 90 casas cujo consumo diário fosse de 450 litros.
d) os moradores dessas casas economizariam mais de R$ 200,00, se o custo de 1 m³ de água para o consumidor fosse igual a R$ 2,50.
e) um reservatório de mesma forma e altura, mas com raio da base 10% menor que o representado, teria água suficiente para abastecer todas as casas.

Exercício 2

(Enem/99) Uma garrafa cilíndrica está fechada, contendo um líquido que ocupa quase completamente seu corpo, conforme mostra a figura. Suponha que, para fazer medições, você disponha apenas de uma régua milimetrada.

Para calcular o volume do líquido contido na garrafa, o número mínimo de medições a serem realizadas é:

a) 1
b) 2
c) 3
d) 4
e) 5

Pratique com 13 exercícios sobre cilindros.