Volume do Prisma: fórmula e exercícios

O volume do prisma é calculado pela multiplicação entre a área da base e a altura.

O volume determina a capacidade que possui uma figura geométrica espacial. Vale lembrar que, geralmente, ele é dado em cm³ (centímetros cúbicos) ou m³ (metros cúbicos).

Fórmula do volume do prisma

Para calcular o volume do prisma utiliza-se a seguinte expressão:

Onde,

A_b: área da base
h: altura

Obs: Não se esqueça que para calcular a área da base é importante saber o formato que a figura apresenta. Por exemplo, num prisma quadrangular a área da base será um quadrado. Já num prisma triangular, a base é formada por um triângulo.

Você Sabia?

O paralelepípedo é um prisma de base quadrangular que tem como base os paralelogramos.

Leia também:

• Prisma
• Poliedro
• Polígonos
• Paralelogramo
• Paralelepípedo
• Geometria Espacial
• Sólidos Geométricos
• Volume do Cilindro
• Volume do Cubo

Exemplo

Calcule o volume de um prisma hexagonal cujo lado da base mede x e sua altura 3x. Note que x é um número dado.

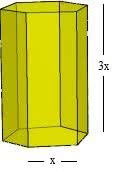
Inicialmente, vamos calcular a área da base para, em seguida, multiplicá-la pela sua altura.

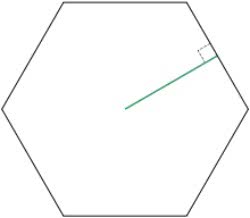
Para isso, precisamos saber do apótema do hexágono, que corresponde à altura do triângulo equilátero:

a = x√3/2

Lembre-se que o apótema é o segmento de reta que parte do centro geométrico da figura e é perpendicular a um dos seus lados.

Logo,

A_b= 3x . x√3/2
A_b = 3√3/2 x²

Por conseguinte, calcula-se o volume do prisma pela fórmula:

V = 3/2 x² √3 . 3x
V = 9√3/2 x³

Exercícios de volume do prisma

Exercício 1

(UE-CE) Com 42 cubos de 1 cm de aresta formamos um paralelepípedo cujo perímetro da base é 18 cm. A altura deste paralelepípedo, em cm, é:

a) 4
b) 3
c) 2
d)1

Exercício 2

(UF-BA) Em relação a um prisma pentagonal regular, é correto afirmar:

(01) O prisma tem 15 arestas e 10 vértices.
(02) Dado um plano que contém uma face lateral, existe uma reta que não intercepta esse plano e contém uma aresta da base.
(04) Dadas duas retas, uma contendo uma aresta lateral e outra contendo uma aresta da base, elas são concorrentes ou reversas.
(08) A imagem de uma aresta lateral por uma rotação de 72° em torno da reta que passa pelo centro de cada uma das bases é outra aresta lateral.
(16) Se o lado da base e a altura do prisma medem, respectivamente, 4,7 cm e 5,0 cm, então a área lateral do prisma é igual a 115 cm².
(32) Se o volume, o lado da base e a altura do prisma medem, respectivamente, 235,0 cm³, 4,7 cm e 5,0 cm, então o raio da circunferência inscrita na base desse prisma mede 4,0 cm.

Exercício 3

(Cefet-MG) De uma piscina retangular com 12 metros de comprimento por 6 metros de largura, foram retirados 10 800 litros de água. É correto afirmar que o nível de água baixou:

a) 15 cm
b) 16 cm
c) 16,5 cm
d) 17 cm
e) 18,5 cm

Exercício 4

(UF-MA) Conta uma lenda que a cidade de Delos, na Grécia Antiga, estava sendo assolada por uma peste que ameaçava matar toda a população. Para erradicar a doença, os sacerdotes consultaram o Oráculo e este ordenou que o altar do Deus Apolo tivesse seu volume duplicado. Sabendo-se que o altar tinha forma cúbica com aresta medindo 1 m, então o valor em que a mesmo deveria ser aumentado era:

a) ³√2
b) 1
c) ³√2 - 1
d) √2 -1
e) 1 - ³√2

Exercício 5

(UE-GO) Uma indústria deseja fabricar um galão no formato de um paralelepípedo retângulo, de forma que duas de suas arestas difiram em 2 cm e a outra meça 30 cm. Para que a capacidade desses galão não seja inferior a 3,6 litros, a menor de suas arestas deve medir no mínimo:

a) 11 cm
b) 10,4 cm
c) 10 cm
d) 9,6 cm

Princípio de Cavalieri

O Princípio de Cavalieri foi criado pelo matemático italiano (1598-1647) Bonaventura Cavalieri no século XVII. É utilizado até hoje para calcular áreas e volumes dos sólidos geométricos.

O enunciado do Princípio de Cavalieri é o seguinte:

“Dois sólidos nos quais todo plano secante, paralelo a um dado plano, determina superfícies de áreas iguais são sólidos de volume iguais.”

Segundo esse princípio, o volume de um prisma é calculado pelo produto da altura pela área da base.