Volume da Pirâmide

Rafael C. Asth

Professor de Matemática e Física

O volume da pirâmide é o espaço ocupado por ela, e sua medida pode ser determinada por cálculos.

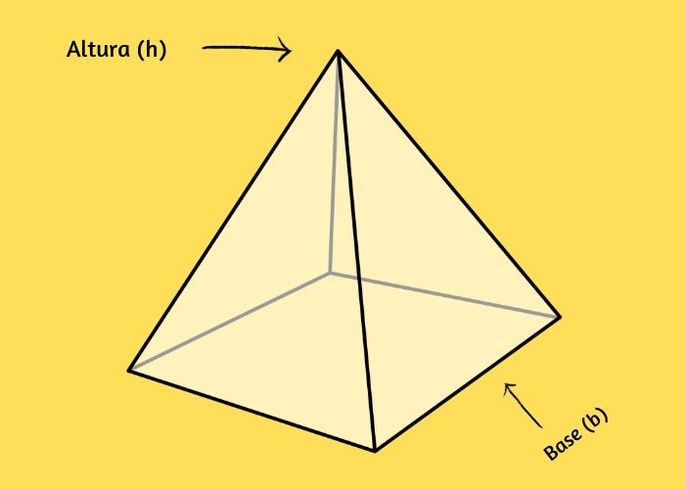
Uma pirâmide é um sólido geométrico de base poligonal com apenas um vértice fora de sua base. Sua altura é determinada pela distância ortogonal (90°) entre o vértice e sua base.

Em relação à base, ela pode ser triangular, pentagonal, quadrada, retangular ou mesmo um polígono não regular.

Para calcular o volume da pirâmide precisamos multiplicar a área da base, o que dependerá de sua forma, pela altura. O resultado desta divisão deve ser dividido por 3.

Fórmula do volume da pirâmide

Para calcular o volume da pirâmide utiliza-se a seguinte fórmula:

$V igual a numerador A com b subscrito. h sobre denominador 3 fim da fração$

Onde,
V: volume da pirâmide
A_b: Área da base
h: altura

Volume da pirâmide quadrada — A altura da pirâmide é calculada a partir da distância de seu vértice até a base

Volume da pirâmide de base triangular

O cálculo do volume de uma pirâmide triangular, também chamada de tetraedro, quando todos os lados são iguais, é feito a partir do cálculo da área do triângulo (base) que está no plano. Em seguida, multiplica-se pela altura e divide-se por três.

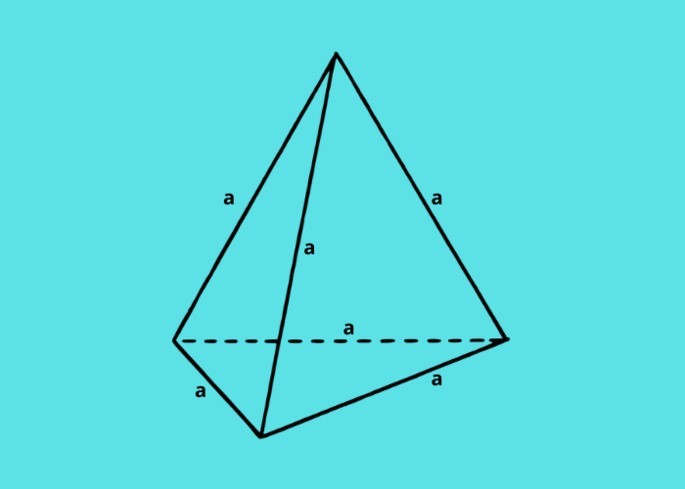
Pirâmide triangular regular (tetraedro) — Numa pirâmide triangular regular todas as arestas possuem a mesma medida

Aplicando o Teorema de Pitágoras duas vezes, para determinar a área da base e após, para a medida da altura, temos:

$V igual a numerador a ao cubo vezes raiz quadrada de 2 sobre denominador 12 fim da fração$

Volume da pirâmide de base quadrada

Em uma pirâmide com base retangular resolve-se, inicialmente a área do retângulo (lado menor x lado maior), multiplica-se pela altura e divide por três.

No caso de uma pirâmide quadrada, a base será um quadrado e a área do quadrado o lado ao quadrado (l²).

Assim sendo:

Pirâmide quadrada

$v igual a numerador l ao quadrado vezes h sobre denominador 3 fim da fração$

Pirâmide retangular

$v igual a numerador l. L. h sobre denominador 3 fim da fração$

3. Pirâmide hexagonal

Do mesmo modo, o volume da pirâmide hexagonal começa a ser resolvido a partir da área de sua base. Relembrando que a fórmula da área de um hexágono é:

$A com h e x subscrito fim do subscrito igual a numerador 3 a ao quadrado raiz quadrada de 3 sobre denominador 2 fim da fração$

Assim sendo, a fórmula do volume da pirâmide hexagonal pode ser compreendida como:

$V igual a numerador l ao quadrado raiz quadrada de 3 sobre denominador 2 fim da fração vezes h$

Exercícios Resolvidos

1. Determine o volume de uma pirâmide regular hexagonal de altura 30 cm e aresta de base de 20 cm.

Resolução:

Primeiramente, temos de encontrar a área da base dessa pirâmide. Nesse exemplo, ela é um hexágono regular de lado l = 20 cm. Logo,

A_b = 6 . l²√3/4
A_b = 6 . 20²√3/4
A_b= 600√3 cm²

Feito isso, podemos substituir o valor da área da base na fórmula do volume:

V = 1/3 A_b.h
V = 1/3 . 600√3 . 30
V = 6000√3 cm³

2. Qual o volume de uma pirâmide regular com 9 m de altura e base quadrada com perímetro de 8 m?

Resolução:

Para resolver esse problema, temos que estar atento ao conceito de perímetro. Ele é a soma de todos os lados de uma figura. Já que se trata de um quadrado, temos que cada lado tem medida de 2 m.

Assim, podemos encontrar a área da base:

A_b= 2² = 4 m

Feito isso, vamos substituir o valor na fórmula do volume da pirâmide:

V = 1/3 A_b.h
V = 1/3 4 . 9
V = 1/3 . 36
V = 36/3
V = 12 m³

Leia mais:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações