ASSINAR TODA MATÉRIA+

Exercícios sobre área e perímetro

Rafael C. Asth
Revisão por Rafael C. Asth
Professor de Matemática e Física

Na Geometria, a área corresponde à medida da superfície, geralmente, calculada pela multiplicação da base pela altura. Já o perímetro é resultado da soma dos lados de uma figura.

Teste seus conhecimentos com 15 questões que criamos sobre o tema e tire suas dúvidas com a resolução após o gabarito.

Questão 1

Calcule o perímetro das figuras planas a seguir segundo as medidas dadas em cada alternativa.

a) Quadrado com lado de 20 cm.

Resposta correta: 80 cm

P = 4.L
P = 4. 20
P = 80 cm

b) Triângulo com dois lados de 6 cm e um lado com 11 cm.

Resposta correta: 23 cm

P = 6 + 6 + 11
P = 23 cm

c) Retângulo com 20 cm de base e 10 cm de altura

Resposta correta: 60 cm

P = 2(b + h)
P = 2(20 + 10)
P = 2.30
P = 60 cm

d) Losango com 8 cm de lado.

Resposta correta: 32 cm

P = 4.L
P = 4 . 8
P = 32 cm

e) Trapézio com base maior de 8 cm, base menor de 4 cm e lados de 6 cm.

Resposta correta: 24 cm

P = B + b + L1 + L2
P = 8 + 4 + 6 + 6
P = 24 cm

f) Círculo com raio de 5 cm.

Resposta correta: P = 10 π cm

P = 2 π . r
P = 2 π . 5
P = 10 π cm

Questão 2

Calcule a área das figuras planas a seguir conforme as medidas dadas em cada alternativa.

a) Quadrado com lado de 20 cm.

Resposta correta: A = 400 cm2

A = L2
A = (20 cm)2
A = 400 cm2

b) Triângulo com 6 cm de base e 12 cm de altura.

Resposta correta: A = 36 cm2

A = b.h/2
A = 6.12/2
A = 72/2
A = 36 cm2

c) Retângulo com 15 cm de base e 10 cm de altura

Resposta correta: 150 cm2

A = b.h
A = 15 . 10
A = 150 cm2

d) Losango com diagonal menor de 7 cm e diagonal maior de 14 cm.

Resposta correta: 49 cm2

A = D.d/2
A = 14 . 7/2
A = 98/2
A = 49 cm2

e) Trapézio com base menor de 4 cm, base maior de 10 cm e altura de 8 cm.

Resposta correta: 56 cm2

A = (B + b) . h/2
A = (10 + 4) . 8/2
A = 14 . 8/2
A = 112/2
A = 56 cm2

f) Círculo com raio de 12 cm.

Resposta correta: 144.π cm2

A = π . r2
A = π . 122
A = 144.π cm2

Questão 3

Juliana possui dois tapetes de mesma área. O tapete quadrado possui lado de 4 m e o tapete retangular tem altura de 2 m e base de 8 m. Qual tapete apresenta o maior perímetro?

a) O tapete quadrado
b) O tapete retangular
c) Os perímetros são iguais

Resposta correta: b) O tapete retangular.

Para saber qual o maior perímetro devemos efetuar o cálculo com os valores dados para os dois tapetes.

Tapete quadrado:

P = 4.L
P = 4.4 m
P = 16 m

Tapete retangular:

P = 2(b+h)
P = 2(8+2)
P = 2.10
P = 20 m

Portanto, o tapete retangular possui o maior perímetro.

Questão 4

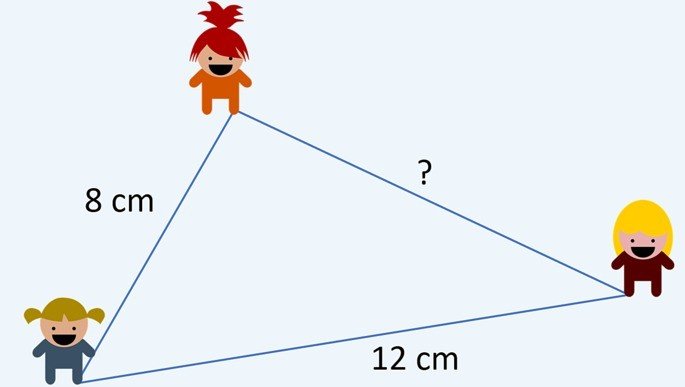
Carla, Ana e Paula estão prontas para iniciar um jogo. Observando a maneira como se organizaram, podemos notar que suas posições formam um triângulo.

Sabendo que o triângulo tem 30 cm de perímetro e Carla está a 8 cm de distância de Ana e Ana está a 12 cm de distância de Paula, qual a distância de Carla e Paula?

Exercícios sobre perímetro

a) 10 cm
b) 11 cm
c) 12 cm
d) 13 cm

Resposta correta: a) 10 cm.

O perímetro de uma figura é a soma dos seus lados. Como o enunciado nos dá o valor do perímetro e de dois lados do triângulo, substituímos na fórmula e encontramos a distância entre Carla e Paula, que corresponde ao terceiro lado do triângulo.

P = a + b + c
30 cm = 8 cm + 12 cm + c
30 cm = 20 cm + c
c = 30 cm – 20 cm
c = 10 cm

Portanto, a distância entre Carla e Paula é de 10 cm.

Questão 5

Seu João resolveu fazer um cercado em sua fazenda com o intuito de plantar algumas verduras. Para impedir que os animais comam seu plantio, ele decidiu cercar a região com arame.

Sabendo que a parte do terreno que seu João utilizou forma um quadrilátero com os lados 50 m, 18 m, 42 m e 16 m, quantos metros de arame seu João precisa comprar para cercar o terreno?

a) 121 m
b) 138 m
c) 126 m
d) 134 m

Resposta correta: c) 126 m.

Se a parte do terreno escolhida para plantar verduras é um quadrilátero de lados 50 m, 18 m, 42 m e 16 m, então a quantidade de arame utilizada pode ser calculada achando o perímetro da figura, pois ele corresponde ao seu contorno.

Como o perímetro é a soma dos lados de uma figura, basta somar os valores dados na questão.

P = 50 m + 18 m + 42 m + 16 m
P = 126 m

Portanto, seu João precisa de 126 metros de arame.

Questão 6

Márcia decidiu pintar uma das paredes de seu quarto com uma cor diferente. Para isso, ela escolheu uma lata de tinta rosa, cujo rótulo diz que o rendimento do conteúdo é 20 m2.

Se a parede que Márcia pretende pintar é retangular, com as medidas de 4 m de comprimento e 3 m de altura, quantas latas de tinta Márcia precisará comprar?

a) uma lata
b) duas latas
c) três latas
d) quatro latas

Resposta correta: a) uma lata.

Para saber a área que será pintada devemos multiplicar a base pela altura.

A = 4 m x 3 m
A = 12 m2

Observe que a parede de Márcia tem uma área de 12 m2 e uma lata de tinta é suficiente para pintar 20 m2, ou seja, mais do que ela precisa.

Portanto, Márcia deverá comprar apenas uma lata de tinta para pintar a parede do seu quarto.

Questão 7

Laura comprou uma peça retangular de tecido e cortou 10 retângulos iguais com altura de 1,5 m e base de 2 m. Qual a área a peça original?

a) 15 m2
b) 25 m2
c) 30 m2
d) 40 m2

Resposta correta: c) 30 m2.

Com os valores dados no enunciado, vamos primeiramente calcular a área de um dos retângulos formados por Laura.

A = b . h
A = 2 m . 1,5 m
A = 3 m2

Já que foram feitos 10 retângulos iguais, então a área da peça inteira é 10x a área de um retângulo.

A = 10 . 3 m2
A = 30 m2

Portanto, a área da peça original é 30 m2.

Questão 8

Pedro está pintando o muro de sua casa, que mede 14,5 m2. Sabendo que Pedro pintou 24 500 cm2 hoje e pretende deixar o restante para amanhã, qual a área, em metros quadrados, que Pedro falta pintar?

a) 10,05 m2
b) 12,05 m2
c) 14, 05 m2
d) 16,05 m2

Resposta correta: b) 12,05 m2.

Para resolver essa questão devemos iniciar convertendo a unidade de área de cm2 para m2.

Se 1 metro tem 100 cm, então 1 metro quadrado tem 100 . 100 cm, que é igual a 10 000 cm2. Sendo assim, dividindo a área dada por 10000 encontraremos o valor em m2.

A = 24 500/10 000 = 2,45 m2

Agora, subtraímos a área pintada da área total do muro para encontrar a região que ainda falta pintar.

14,5 m2 – 2,45 m2 = 12,05 m2

Sendo assim, resta para Pedro pintar 12,05 m2 do muro.

Questão 9

Lucas decidiu vender seu carro e, para conseguir um comprador rapidamente, resolveu colocar um anúncio no jornal da cidade. Sabendo que é pedido R$ 1,50 por centímetro quadrado de publicidade, quanto Lucas teve que pagar por um anúncio retangular de base 5 cm e altura de 4 cm?

a) R$ 15,00
b) R$ 10,00
c) R$ 20,00
d) R$ 30,00

Resposta correta: d) R$ 30,00.

Primeiramente, devemos calcular a área do anúncio criado por Lucas.

A = b.h
A = 5 cm . 4 cm
A = 20 cm2

O preço pago pode ser encontrado multiplicando a área pelo preço pedido.

Preço = 20 . R$ 1,50 = R$ 30,00

Sendo assim, o anúncio de Lucas custará R$ 30,00.

Questão 10

Paulo decidiu aproveitar o espaço não utilizado do seu quarto para construir um banheiro. Conversando com um arquiteto, Paulo descobriu que para o cômodo com vaso sanitário, pia e chuveiro ele precisaria de uma área mínima de 3,6 m2.

Respeitando as indicações do arquiteto, qual das figuras abaixo representa a planta correta para o banheiro de Paulo?

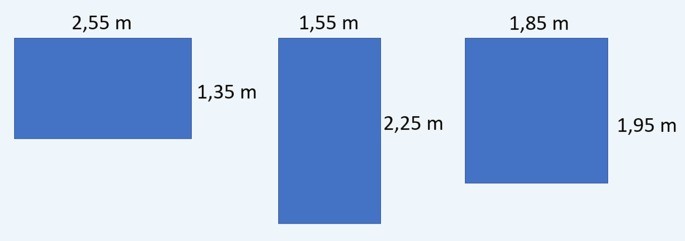
Exercício sobre área

a) 2,55 m x 1,35 m
b) 1,55 m x 2,25 m
c) 1,85 m x 1,95 m

Resposta correta: c) 1,85 m x 1,95 m.

Para responder a essa pergunta vamos calcular a área das três figuras

A = 2,55 x 1,35
A = 3,4425 m2

A = 1,55 x 2,25
A = 3,4875 m2

A = 1,85 x 1,95
A = 3,6075 m2

Sendo assim, a melhor escolha para o banheiro de Paulo é a opção com 1,85 m x 1,95 m.

Questão 11

Para produzir uma escultura em aço, uma placa retangular com medidas de 0,8 m de largura e 1,2 m de comprimento foi cortada nas linhas tracejadas. Um corte foi realizado entre os pontos médios da largura e do comprimento, o outro, de um vértice até a metade da largura. A área cinza da placa da escultura possui quantos centímetros quadrados?

Imagem associada a questão.

Resposta: 6 000 cm²

Para calcular a área cinza podemos calcular a área total do retângulo e subtrair a área dos triângulos.

Área do retângulo em centímetros quadrados.

A = largura x comprimento = 80 cm x 120 cm = 9 600 cm²

Área do triângulo de cima.

Como a linha tracejada foi desenhada a partir dos pontos médios, altura e base do triângulos são as metades das medidas do retângulo.

reto A igual a numerador reto b. reto h sobre denominador 2 fim da fração reto A igual a numerador 60 espaço. espaço 40 sobre denominador 2 fim da fração igual a 1 espaço 200 espaço cm ao quadrado

Área do retângulo de baixo.

reto A igual a numerador reto b espaço. espaço reto h sobre denominador 2 fim da fração reto A espaço igual a espaço numerador 120 espaço. espaço 40 sobre denominador 2 fim da fração reto A espaço igual a 2 espaço 400 espaço cm ao quadrado

Cálculo da área final

Área do retângulo - área do triângulo de cima - área do triângulo de baixo.

9 600 - 1 200 - 2 400 = 6 000 cm²

Questão 12

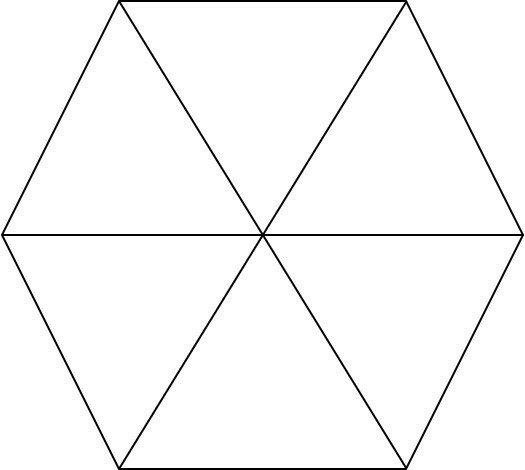
Um hexágono regular foi construído pelo arranjo de seis triângulos equiláteros de área 8 cm². Determine o perímetro do hexágono. Considere raiz quadrada de 3 aproximadamente igual 1 vírgula 73.

Resposta: 25,8 cm

Um hexágono regular pode ser obtido por seis triângulos equiláteros (três lados iguais), assim:

Imagem associada a questão.

Para determinar seu perímetro, precisamos determinar a medida do lado do triângulo e, por fim, multiplicar por seis.

Como a área do triângulo é de 8 cm², usando a fórmula da área do triângulo equilátero:

reto A igual a numerador reto L ao quadrado. raiz quadrada de 3 sobre denominador 4 fim da fração

Substituindo a área por 8 e resolvendo para L, temos:

8 igual a numerador reto L ao quadrado. raiz quadrada de 3 sobre denominador 4 fim da fração 32 igual a reto L ao quadrado. raiz quadrada de 3 numerador 32 sobre denominador raiz quadrada de 3 fim da fração igual a reto L ao quadrado

Substituindo o valor da raiz de 3 para 1,73:

numerador 32 sobre denominador raiz quadrada de 3 fim da fração igual a reto L ao quadrado numerador 32 sobre denominador 1 vírgula 73 fim da fração igual a reto L ao quadrado 18 vírgula 49 igual a reto L ao quadrado raiz quadrada de 18 vírgula 49 fim da raiz igual a reto L 4 vírgula 3 aproximadamente igual reto L

Para determinar o perímetro, é preciso multiplicar o resultado por 6.

P igual a 4 vírgula 3 espaço. espaço 6 espaço igual a espaço 25 vírgula 8 espaço c m

Questão 13

Conteúdo exclusivo para assinantes Toda Matéria+
Além de mais exercícios, tenha acesso a mais recursos para dar um up nos seus estudos.
Corretor de Redação para o Enem
Exercícios exclusivos
Estude sem publicidade
Assinar Toda Matéria+

Continue praticando com:

Estude mais sobre:

Rafael C. Asth
Revisão por Rafael C. Asth
Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.
Veja também
Leitura Recomendada
Tópicos Relacionados
Exercícios Exercícios de Matemática Matemática Geometria 1º ano (Ensino Médio)
Que tal um up?
Toda Matéria+
Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo
Exercícios exclusivos Acesso a centenas de questões com gabaritos
Estude sem publicidade Navegação limpa e focada para evitar distrações
Assinar Toda Matéria+
Toda Matéria no YouTube
Thumbnail Toda Matéria no Youtube
Toda Matéria Inscreva-se