Exercícios de cone (com respostas explicadas)
Os cones são sólidos geométricos de revolução que têm como características uma base circular e um vértice. Pratique este tema com esta lista de exercícios sobre cones e tire suas dúvidas com as respostas explicadas.
Questão 1
Determine o volume de um cone com raio da base de 6 cm e altura de 5 cm.
Utilize .
Questão 2
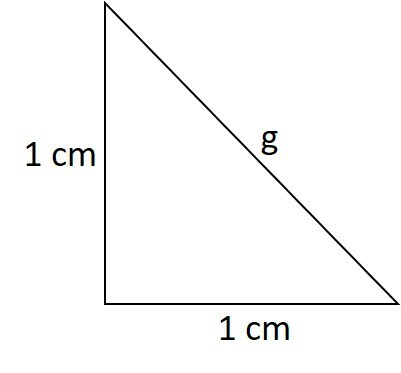
Determine a área total de um sólido de revolução formado a partir de um triângulo retângulo isósceles de catetos iguais a 1 cm.
Questão 3
Em um cone com volume de cm³ e raio da base de 3 cm, determine a medida de sua geratriz. Utilize
.
Questão 4
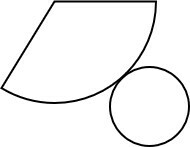
Em festas de aniversário é comum o uso de um chapéu em forma de um cone. Para sua fabricação é utilizado uma folha plana de papel, como no molde a seguir.
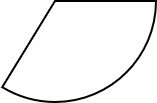
Para produzir um chapéu na forma de cone com raio da base com 10 cm e altura de 15 cm, qual deve ser a área do molde?
Questão 5
(EsPCEx 2014) Um cone de revolução tem altura 4 cm e está circunscrito a uma esfera de raio 1 cm. O volume desse cone (em cm³) é igual a
a)
b)
c)
d)
e) 3
Para determinar o volume do cone, é necessário obter o raio da base.
A vista lateral da figura é:
imagem
Identificamos um par de triângulos semelhantes. Pela proporção de seus lados, obtemos o raio da base.
No triângulo retângulo maior, a base é o raio R e a altura é 4 cm.
No triângulo retângulo menor a altura é x, a hipotenusa é 3 cm e a base 1 cm. Pelo teorema de Pitágoras:
Montando a proporção entre lados correspondentes:
Racionalizando:
Substituindo o raio na fórmula de volume:
Questão 6
(UFU-MG 2017) Um recipiente cônico utilizado em experiências de química deve ter duas marcas horizontais circulares, uma situada a 1 centímetro do vértice do cone, marcando um certo volume v, e outra marcando o dobro deste volume, situada H a centímetros do vértice, conforme figura.
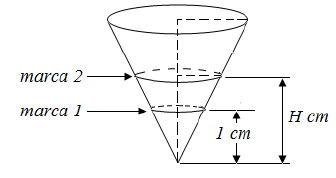
Nestas condições, a distância H, em centímetros, é igual a:
a)
b) √3
c) 4/3
d) 3/2
A relação entre os volumes é igual à relação cúbica das alturas.
Questão 7
(Enem 2021) No desenho técnico, é comum representar um sólido por meio de três vistas (frontal, perfil e superior), resultado da projeção do sólido em três planos, perpendiculares dois a dois.
A figura representa as vistas de uma torre.
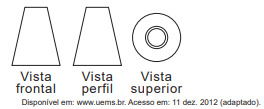
Com base nas vistas fornecidas, qual figura melhor representa essa torre?
a) 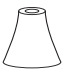
b) 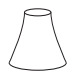
c) 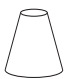
d) 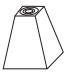
e) 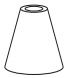
As vistas frontal e de perfil são iguais, sendo troncos de cone. Ainda, a vista superior mostra uma dupla circunferência, sendo o gabarito a opção e.
Questão 8
(Enem 2021) Nas empresas em geral, são utilizados dois tipos de copos plásticos descartáveis, ambos com a forma de troncos de cones circulares retos:
• copos pequenos, para a ingestão de café: raios das bases iguais a 2,4 cm e 1,8 cm e altura igual a 3,6 cm;
• copos grandes, para a ingestão de água: raios das bases iguais a 3,6 cm e 2,4 cm e altura igual a 8,0 cm.
Uma dessas empresas resolve substituir os dois modelos de copos descartáveis, fornecendo para cada um de seus funcionários canecas com a forma de um cilindro circular reto de altura igual a 6 cm e raio da base de comprimento igual a y centímetros. Tais canecas serão usadas tanto para beber café como para beber água.
Sabe-se que o volume de um tronco de cone circular reto, cujos raios das bases são respectivamente iguais a R e r e a altura é h, é dado pela expressão:
O raio y da base dessas canecas deve ser tal que y² seja, no mínimo, igual a
a) 2,664 cm.
b) 7,412 cm.
c) 12,160 cm.
d) 14,824 cm.
e) 19,840 cm.
O raio da base der possuir uma medida mínima que permita o consumo da água, equivalente ao copo em forma de tronco de cone maior.
Satisfazendo esta condição, a do café já está automaticamente atendida.
O volume da caneca em forma de cilindro deve ser, pelo menos, igual ao do copo grande.
Veja também:
Siga praticando com:
- Índice de exercícios de matemática do 2º ano do Ensino Médio
- Exercícios sobre cilindros (com respostas)
ASTH, Rafael. Exercícios de cone (com respostas explicadas). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-de-cone/. Acesso em: