Exercícios de Desvio Padrão (com questões explicadas)

Rafael C. Asth

Professor de Matemática e Física

Estude e tire suas dúvidas sobre desvio padrão com os exercícios respondidos e explicados.

Questão 1

Uma escola está organizando uma olimpíada onde uma das provas é uma corrida. Os tempos que cinco alunos levaram para completar a prova, em segundos, foram:

23, 25, 28, 31, 32, 35

O desvio padrão dos tempos de prova dos alunos foi:

Ver Resposta

Resposta: Aproximadamente 3,91.

O desvio padrão pode ser calculado pela fórmula:

$DP igual a raiz quadrada de numerador começar estilo mostrar soma de reto i igual a 1 para reto n de fim do estilo parêntese esquerdo reto x com reto i subscrito menos MA parêntese direito ao quadrado sobre denominador reto n fim da fração fim da raiz$

Sendo,

∑: símbolo de somatório. Indica que temos que somar todos os termos, desde a primeira posição (i=1) até a posição n.
x_i: valor na posição i no conjunto de dados.
M_A: média aritmética dos dados.
n: quantidade de dados.

Vamos resolver cada passo da fórmula separadamente, para tornar mais fácil a compreensão.

Para o cálculo do desvio padrão é necessário calcular a média aritmética.

$MA igual a numerador 23 espaço mais espaço 25 espaço mais espaço 28 espaço mais espaço 31 espaço mais espaço 32 espaço mais espaço 35 sobre denominador 6 fim da fração igual a 174 sobre 6 igual a 29$

Fazemos agora a soma da subtração de cada termo pela média, elevado ao quadrado.

$parêntese esquerdo 23 espaço menos espaço 29 parêntese direito ao quadrado mais parêntese esquerdo 25 menos 29 parêntese direito ao quadrado mais parêntese esquerdo 28 menos 29 parêntese direito ao quadrado mais parêntese esquerdo 31 menos 29 parêntese direito ao quadrado mais parêntese esquerdo 32 menos 29 parêntese direito ao quadrado mais parêntese esquerdo 35 menos 29 parêntese direito ao quadrado igual a espaço parêntese esquerdo menos 6 parêntese direito ao quadrado mais parêntese esquerdo menos 4 parêntese direito ao quadrado mais parêntese esquerdo menos 1 parêntese direito ao quadrado mais 2 ao quadrado mais 3 ao quadrado mais 6 ao quadrado igual a 36 mais 16 mais 1 mais 4 mais 9 mais 36 igual a 102$

Dividimos o valor desta soma pelo número de elementos somados.

$102 sobre 6 igual a 17$

Por último, retiramos a raiz quadrada deste valor.

$raiz quadrada de 17 aproximadamente igual 4 vírgula 12$

Questão 2

Uma mesma avaliação foi aplicada à quatro grupos com quantidades diferentes de pessoas. As notas mínima e máxima de cada grupo estão dispostas na tabela.

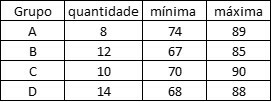
Considerando a média de cada grupo como a média aritmética entre a nota mínima e a máxima, determine o desvio padrão das notas em relação aos grupos.

Considerar até a segunda casa decimal, para simplificação dos cálculos.

Ver Resposta

Resposta: aproximadamente 1,03.

O desvio padrão pode ser calculado pela fórmula:

Como as quantidades são diferentes em cada grupo, fazemos a média aritmética de cada um, depois a ponderada entre os grupos.

Médias aritméticas

$A dois pontos espaço parêntese esquerdo 89 menos 74 parêntese direito dividido por 2 igual a 7 vírgula 5 B dois pontos espaço parêntese esquerdo 85 menos 67 parêntese direito dividido por 2 igual a 9 C dois pontos espaço parêntese esquerdo 90 menos 70 parêntese direito dividido por 2 igual a 10 D dois pontos espaço parêntese esquerdo 88 menos 68 parêntese direito dividido por 2 igual a 10$

Média ponderada entre os grupos

$M P igual a espaço numerador 7 vírgula 5 espaço. espaço 8 espaço mais espaço 9 espaço. espaço 12 espaço mais espaço 10 espaço. espaço 10 espaço mais espaço 10 espaço. espaço 14 sobre denominador 8 mais 12 mais 10 mais 14 fim da fração M P igual a numerador 60 mais 108 mais 100 mais 140 sobre denominador 44 fim da fração M P igual a 408 sobre 44 aproximadamente igual 9 vírgula 27$

Cálculo do termo:

$soma de reto i igual a 1 para reto n de parêntese esquerdo reto x com reto i subscrito menos M P parêntese direito ao quadrado$ , onde xi é a média de cada grupo.

$parêntese esquerdo 7 vírgula 5 menos 9 vírgula 27 parêntese direito ao quadrado mais parêntese esquerdo 9 menos 9 vírgula 27 parêntese direito ao quadrado mais parêntese esquerdo 10 menos 9 vírgula 27 parêntese direito ao quadrado mais parêntese esquerdo 10 menos 9 vírgula 27 parêntese direito ao quadrado igual a espaço abre parênteses menos 1 vírgula 77 fecha parênteses ao quadrado mais parêntese esquerdo menos 0 vírgula 27 parêntese direito ao quadrado mais parêntese esquerdo 0 vírgula 73 parêntese direito ao quadrado mais parêntese esquerdo 0 vírgula 73 parêntese direito ao quadrado igual a espaço 3 vírgula 13 mais 0 vírgula 07 mais 0 vírgula 53 mais 0 vírgula 53 igual a 4 vírgula 26$

Dividindo o valor da soma pelo número de grupos:

$numerador 4 vírgula 26 sobre denominador 4 fim da fração igual a 1 vírgula 06$

Retirando a raiz quadrada

$raiz quadrada de 1 vírgula 06 fim da raiz aproximadamente igual 1 vírgula 03$

Questão 3

Afim de implantar um controle de qualidade, uma indústria que produz cadeados realizou um monitoramento de sua produção diária por uma semana de trabalho. Eles registraram o número de cadeados defeituosos produzidos a cada dia. Os dados foram os seguintes:

segunda-feira: 5 peças defeituosas
terça-feira: 8 peças defeituosas
quarta-feira: 6 peças defeituosas
quinta-feira: 7 peças defeituosas
sexta-feira: 4 peças defeituosas

Calcule o desvio padrão do número de peças defeituosas produzidas durante essa semana.

Considere até a segunda casa decimal.

Ver Resposta

Resposta: Aproximadamente 1,41.

Para o cálculo do desvio padrão vamos calcular a média entre os valores.

$MA igual a numerador 5 mais 8 mais 6 mais 7 mais 4 sobre denominador 5 fim da fração igual a 30 sobre 5 igual a 6$

Utilizando a fórmula do desvio padrão:

$DP igual a raiz quadrada de numerador começar estilo mostrar soma de reto i igual a 1 para reto n de parêntese esquerdo reto x com reto i subscrito menos MA parêntese direito ao quadrado fim do estilo sobre denominador reto n fim da fração fim da raiz DP igual a raiz quadrada de numerador começar estilo mostrar parêntese esquerdo 5 menos 6 parêntese direito ao quadrado mais parêntese esquerdo 8 menos 6 parêntese direito ao quadrado mais parêntese esquerdo 6 menos 6 parêntese direito ao quadrado mais parêntese esquerdo 7 menos 6 parêntese direito ao quadrado mais parêntese esquerdo 4 menos 6 parêntese direito ao quadrado fim do estilo sobre denominador 5 fim da fração fim da raiz DP igual a raiz quadrada de numerador começar estilo mostrar parêntese esquerdo menos 1 parêntese direito ao quadrado mais 2 ao quadrado mais 0 ao quadrado mais 1 ao quadrado mais parêntese esquerdo menos 2 parêntese direito ao quadrado fim do estilo sobre denominador 5 fim da fração fim da raiz DP igual a raiz quadrada de numerador começar estilo mostrar 1 mais 4 mais 0 mais 1 mais 4 fim do estilo sobre denominador 5 fim da fração fim da raiz DP igual a raiz quadrada de numerador começar estilo mostrar 10 fim do estilo sobre denominador 5 fim da fração fim da raiz igual a raiz quadrada de 2 aproximadamente igual 1 vírgula 41$

Questão 4

Uma loja de brinquedos fez um levantamento sobre o faturamento da empresa ao longo de um ano e obteve os seguintes dados, em milhares de reais.

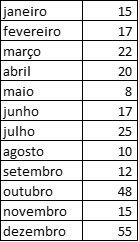
Determine o desvio padrão do faturamento da empresa ao longo deste ano.

Ver Resposta

Resposta: aproximadamente 14,04.

Calculando a média aritmética:

$MA igual a numerador 15 mais 17 mais 22 mais 20 mais 8 mais 17 mais 25 mais 10 mais 12 mais 48 mais 15 mais 55 sobre denominador 12 fim da fração MA igual a 264 sobre 12 igual a 22$

Aplicando na fórmula do desvio padrão:

Para o cálculo do somatório:

$parêntese esquerdo 15 menos 22 parêntese direito ao quadrado igual a 49 parêntese esquerdo 17 menos 22 parêntese direito ao quadrado igual a 25 parêntese esquerdo 22 menos 22 parêntese direito ao quadrado igual a 0 parêntese esquerdo 20 menos 22 parêntese direito ao quadrado igual a 4 parêntese esquerdo 8 menos 22 parêntese direito ao quadrado igual a 196 parêntese esquerdo 17 menos 22 parêntese direito ao quadrado igual a 25 parêntese esquerdo 25 menos 22 parêntese direito ao quadrado igual a 9 parêntese esquerdo 10 menos 22 parêntese direito ao quadrado igual a 144 parêntese esquerdo 12 menos 22 parêntese direito ao quadrado igual a 100 parêntese esquerdo 48 menos 22 parêntese direito ao quadrado igual a 676 parêntese esquerdo 15 menos 22 parêntese direito ao quadrado igual a 49 parêntese esquerdo 55 menos 22 parêntese direito ao quadrado igual a 1089$

Somando todas as parcelas temos 2366.

Aplicando na fórmula do desvio padrão:

$DP igual a raiz quadrada de numerador começar estilo mostrar 2366 fim do estilo sobre denominador 12 fim da fração fim da raiz aproximadamente igual raiz quadrada de 197 vírgula 16 fim da raiz aproximadamente igual 14 vírgula 04$

Questão 5

Uma pesquisa está sendo realizada visando conhecer a melhor variedade de uma planta para produção agrícola. Cinco amostras de cada variedade foram plantadas nas mesmas condições. A regularidade nos seus desenvolvimentos é uma característica importante para produção em escala.

Suas alturas após um determinado tempo estão abaixo e, a variedade da planta com maior regularidade será escolhida para produção.

Variedade A:

Planta 1: 50 cm
Planta 2: 48 cm
Planta 3: 52 cm
Planta 4: 51 cm
Planta 5: 49 cm

Variedade B:

Planta 1: 57 cm
Planta 2: 55 cm
Planta 3: 59 cm
Planta 4: 58 cm
Planta 5: 56 cm

É possível chegar a uma escolha através do cálculo do desvio padrão?

Ver Resposta

Resposta: Não é possível, pois ambas as variedades apresentam o mesmo desvio padrão.

Média aritmética de A

$MA igual a numerador 50 mais 48 mais 52 mais 51 mais 49 sobre denominador 5 fim da fração igual a 250 sobre 5 igual a 50$

Desvio padrão de A

$DP igual a raiz quadrada de numerador começar estilo mostrar soma de reto i igual a 1 para reto n de parêntese esquerdo reto x com reto i subscrito menos MA parêntese direito ao quadrado fim do estilo sobre denominador reto n fim da fração fim da raiz DP igual a raiz quadrada de numerador começar estilo mostrar parêntese esquerdo 50 menos 50 parêntese direito ao quadrado mais parêntese esquerdo 48 menos 50 parêntese direito ao quadrado mais parêntese esquerdo 52 menos 50 parêntese direito ao quadrado mais parêntese esquerdo 51 menos 50 parêntese direito ao quadrado mais parêntese esquerdo 49 menos 50 parêntese direito ao quadrado fim do estilo sobre denominador 5 fim da fração fim da raiz DP igual a raiz quadrada de numerador começar estilo mostrar 0 ao quadrado mais parêntese esquerdo menos 2 parêntese direito ao quadrado mais 2 ao quadrado mais 1 ao quadrado mais parêntese esquerdo menos 1 parêntese direito ao quadrado fim do estilo sobre denominador 5 fim da fração fim da raiz DP igual a raiz quadrada de numerador começar estilo mostrar 0 mais 4 mais 4 mais 1 mais 1 fim do estilo sobre denominador 5 fim da fração fim da raiz DP igual a raiz quadrada de numerador começar estilo mostrar 10 fim do estilo sobre denominador 5 fim da fração fim da raiz igual a raiz quadrada de 2 aproximadamente igual 1 vírgula 41$

Média aritmética de B

$M A igual a numerador 57 mais 55 mais 59 mais 58 mais 56 sobre denominador 5 fim da fração igual a 285 sobre 5 igual a 57$

Desvio padrão de B

$DP igual a raiz quadrada de numerador começar estilo mostrar soma de reto i igual a 1 para reto n de parêntese esquerdo reto x com reto i subscrito menos MA parêntese direito ao quadrado fim do estilo sobre denominador reto n fim da fração fim da raiz DP igual a raiz quadrada de numerador começar estilo mostrar parêntese esquerdo 57 menos 57 parêntese direito ao quadrado mais parêntese esquerdo 55 menos 57 parêntese direito ao quadrado mais parêntese esquerdo 59 menos 57 parêntese direito ao quadrado mais parêntese esquerdo 58 menos 57 parêntese direito ao quadrado mais parêntese esquerdo 56 menos 57 parêntese direito ao quadrado fim do estilo sobre denominador 5 fim da fração fim da raiz DP igual a raiz quadrada de numerador começar estilo mostrar 0 mais abre parênteses menos 2 fecha parênteses ao quadrado mais 2 ao quadrado mais 1 ao quadrado mais parêntese esquerdo menos 1 parêntese direito ao quadrado fim do estilo sobre denominador 5 fim da fração fim da raiz DP igual a raiz quadrada de numerador começar estilo mostrar 0 mais 4 mais 4 mais 1 mais 1 fim do estilo sobre denominador 5 fim da fração fim da raiz DP igual a raiz quadrada de numerador começar estilo mostrar 10 fim do estilo sobre denominador 5 fim da fração fim da raiz igual a raiz quadrada de 2 igual a 1 vírgula 41$

Questão 6

Em um certo teste para concorrer a um papel em uma peça de teatro, dois candidatos participaram e foram avaliados por quatro jurados, onde cada um forneceu as seguintes notas:

Candidato A: 87, 69, 73, 89
Candidato B: 87, 89, 92, 78

Determine o candidato com a maior média e o menor desvio padrão.

Ver Resposta

Resposta: O candidato B teve a maior média e o menor desvio padrão.

Média do candidato A

$MA igual a numerador 87 mais 69 mais 73 mais 89 sobre denominador 4 fim da fração MA igual a 318 sobre 4 MA igual a 79 vírgula 5$

Média do candidato B

$MB igual a numerador 87 mais 89 mais 92 mais 78 sobre denominador 4 fim da fração MB igual a 346 sobre 4 MB igual a 86 vírgula 5$

Desvio padrão de A

$DP igual a raiz quadrada de numerador começar estilo mostrar soma de reto i igual a 1 para reto n de parêntese esquerdo reto x com reto i subscrito menos MA parêntese direito ao quadrado fim do estilo sobre denominador reto n fim da fração fim da raiz DP igual a raiz quadrada de numerador começar estilo mostrar parêntese esquerdo 87 menos 79 vírgula 5 parêntese direito ao quadrado mais parêntese esquerdo 69 menos 89 parêntese direito ao quadrado mais parêntese esquerdo 73 menos 92 parêntese direito ao quadrado mais parêntese esquerdo 89 menos 75 parêntese direito ao quadrado fim do estilo sobre denominador 4 fim da fração fim da raiz DP igual a raiz quadrada de numerador 56 vírgula 25 mais 400 mais 361 mais 196 sobre denominador 4 fim da fração fim da raiz DP igual a raiz quadrada de numerador 1.013 vírgula 25 sobre denominador 4 fim da fração fim da raiz DP igual a raiz quadrada de 506 vírgula 62 fim da raiz DP igual a 22 vírgula 5$

Desvio padrão de B

$DP igual a raiz quadrada de numerador começar estilo mostrar soma de reto i igual a 1 para reto n de parêntese esquerdo reto x com reto i subscrito menos MB parêntese direito ao quadrado fim do estilo sobre denominador reto n fim da fração fim da raiz DP igual a raiz quadrada de numerador começar estilo mostrar parêntese esquerdo 87 menos 86 vírgula 5 parêntese direito ao quadrado mais abre parênteses 89 menos 86 vírgula 5 fecha parênteses ao quadrado mais abre parênteses 92 menos 86 vírgula 5 fecha parênteses ao quadrado mais abre parênteses 78 menos 86 vírgula 5 fecha parênteses ao quadrado fim do estilo sobre denominador 4 fim da fração fim da raiz DP igual a raiz quadrada de numerador 0 vírgula 25 mais 6 vírgula 25 mais 30 vírgula 25 mais 72 vírgula 25 sobre denominador 4 fim da fração fim da raiz DP igual a raiz quadrada de 109 sobre 4 fim da raiz DP igual a raiz quadrada de 27 vírgula 25 fim da raiz DP aproximadamente igual 5 vírgula 22$

Questão 7

(UFBA) Durante um dia de trabalho, um pediatra atendeu, em seu consultório, cinco crianças com sintomas compatíveis a gripe. Ao fim do expediente, ele produziu um quadro com o número de dias que cada uma das crianças teve febre, antes da consulta

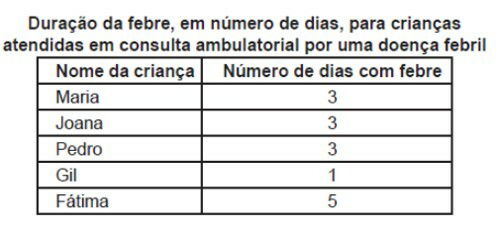
Com base nesses dados, pode-se afirmar:

O desvio padrão para o número de dias de febre para essas crianças foi maior do que dois.

Certo

Errado

Questão 8

(UNB)

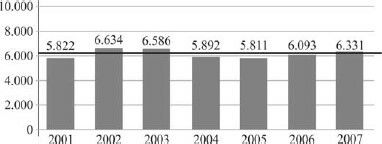
O gráfico acima mostra a quantidade de internações de usuários de drogas com até 19 anos de idade, no Brasil, no período de 2001 a 2007. O número médio de internações no período, indicado pela linha em negrito, foi igual a 6.167.

Assinale a opção que apresenta a expressão que permite determinar-se corretamente o desvio-padrão — R — da série de dados indicados no gráfico.

a) $7 reto R ao quadrado espaço igual a espaço 345 ao quadrado espaço mais espaço 467 ao quadrado espaço mais espaço 419 à potência de 2 espaço fim do exponencial mais espaço 275 ao quadrado espaço mais espaço 356 ao quadrado espaço mais espaço 74 ao quadrado espaço mais espaço 164 ao quadrado$

b) $7 reto R espaço igual a espaço √ 345 espaço mais espaço √ 467 espaço mais espaço √ 419 espaço mais espaço √ 275 espaço mais espaço √ 356 espaço mais espaço √ 74 espaço mais espaço √ 164$

c) $espaço 6.167 R ao quadrado igual a 5.822 ao quadrado espaço mais espaço 6.634 ao quadrado espaço mais espaço 6.586 ao quadrado espaço mais espaço 5.892 ao quadrado espaço mais espaço 5.811 ao quadrado mais espaço 6.093 ao quadrado espaço mais espaço 6.331 ao quadrado$

d) $6.167 reto R igual a √ 5.822 mais √ 6.634 mais √ 6.586 mais √ 5.892 mais √ 5.811 mais √ 6.093 mais √ 6.331$

Questão 9

(Enem 2019) Um fiscal de certa empresa de ônibus registra o tempo, em minuto, que um motorista novato gasta para completar certo percurso. No Quadro 1 figuram os tempos gastos pelo motorista ao realizar o mesmo percurso sete vezes. O Quadro 2 apresenta uma classificação para a variabilidade do tempo, segundo o valor do desvio padrão.

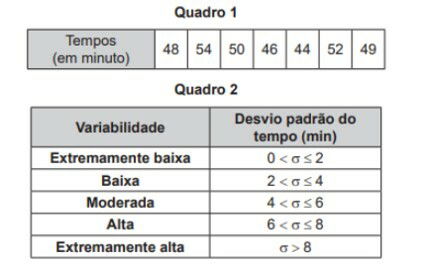
Com base nas informações apresentadas nos quadros, a variabilidade do tempo é

a) extremamente baixa.

b) baixa.

c) moderada.

d) alta.

e) extremamente alta.

Questão 10

(Enem 2021) Um zootecnista pretende testar se uma nova ração para coelhos é mais eficiente do que a que ele vem utilizando atualmente. A ração atual proporciona uma massa média de 10 kg por coelho, com um desvio padrão de 1 kg, alimentado com essa ração durante um período de três meses.

O zootecnista selecionou uma amostra de coelhos e os alimentou com a nova ração pelo mesmo período de tempo. Ao final, anotou a massa de cada coelho, obtendo um desvio padrão de 1,5 kg para a distribuição das massas dos coelhos dessa amostra.

Para avaliar a eficiência dessa ração, ele utilizará o coeficiente de variação (CV) que é uma medida de dispersão definida por CV = $numerador reto S sobre denominador reto X em moldura superior fim da fração$ , em que s representa o desvio padrão e $reto X em moldura superior$ , a média das massas dos coelhos que foram alimentados com uma determinada ração.

O zootecnista substituirá a ração que vinha utilizando pela nova, caso o coeficiente de variação da distribuição das massas dos coelhos que foram alimentados com a nova ração for menor do que o coeficiente de variação da distribuição das massas dos coelhos que foram alimentados com a ração atual.

A substituição da ração ocorrerá se a média da distribuição das massas dos coelhos da amostra, em quilograma, for superior a

a) 5,0

b) 9,5

c) 10,0

d) 10,5

e) 15,0

Aprenda mais sobre desvio padrão.

Pratique com:

Siga aprendendo e praticando com:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.