Exercícios de Matemática 9º ano com respostas
Pratique com os exercícios de matemática para o 9º ano com gabarito. Veja as matérias que você estuda na escola e tire suas dúvidas com os exercícios resolvidos passo a passo.
Os professores podem utilizá-los em suas aulas e atividades. Todos os exercícios são baseados na BNCC e estão com o código da habilidade.
Exercício 1 (Potências com expoentes negativos e fracionários)
Habilidade BNCC EF09MA03
Resolva a expressão que envolve potências com expoente negativo e fracionário.
Exercício 2 (Notação científica)
Habilidade BNCC EF09MA04
Em uma distribuidora de material para escritório, há 120 pilhas de folhas A4 com 1 m de altura cada. Estas folhas estão em resmas (quinhentas folhas). Na embalagem, o fornecedor indica que a espessura de uma folha é 0,4 mm. O gerente da distribuidora fez um levantamento e identificou que o número de folhas e de resmas são, respectivamente,
a) 600 000 folhas e 1 200 resmas.
b) 120 000 folhas e 240 resmas.
c) 300 000 folhas e 600 resmas.
d) 100 000 folhas e 200 resmas.
Objetivo
Número de folhas e de resmas.
Dados
120 pilhas
1 m de altura cada pilha.
Espessura da folha igual a 0,4 mm.
Resolução
Como as unidades estão em múltiplos diferentes, é preciso igualá-las.
1 m = 1 000 mm
O número de folhas em uma pilha é a divisão entre 1 000 mm e 0,4 mm. Para facilitar o cálculo podemos transformar as medidas em notação científica.
Como há 120 pilhas, basta multiplicar.
Há 300 000 folhas no depósito.
Para calcular o número de resmas, basta dividir por 500.
Havendo 600 resmas no depósito.
Exercício 3 (Porcentagem)
Habilidade BNCC EF09MA05
Um serviço de filmes e séries por assinatura lançou uma promoção visando conquistar mais clientes. Caso um cliente indique um novo, recebe um desconto de 10% em suas mensalidades. Para o segundo cliente indicado que fechar uma assinatura, o indicador recebe mais 10% em relação ao preço que pagava, após a primeira indicação.
Se o preço inicial da assinatura era de R$35,00, após duas indicações, o cliente indicador pagará
a) R$28,00
b) R$28,35
c) R$17,00
d) R$30,00
Descontar 10% é multiplicar por 0,90, pois:
Como os descontos ocorrem em duas etapas, temos:
Assim, o cliente pagará R$28,35 após a segunda indicação.
Exercício 4 (Funções)
Habilidade BNCC EF09MA06
Em uma cooperativa de artesanato são fabricadas cestas feitas de Capim Dourado. Um dia de trabalho tem um custo fixo de R$150,00, mais R$36,00 por cesta fabricada. Um único artesão consegue produzir um número máximo de nove cestas em um dia de trabalho. O custo total de um dia de trabalho depende do número de cestas fabricadas.
A expressão algébrica que descreve a relação entre o número de cestas, o custo de um dia de trabalho e o custo da produção de nove cestas é de
a) C(n) = 150 + n; R$ 186,00
b) C(n) = 36n; R$ 1 296,00
c) C(n) = 150 + 36n; R$ 474,00
d) C(n) = 36 + 9n; R$ 360,00
O custo depende da quantidade de cestas produzidas, sendo R$36,00 a cada unidade mais o custo fixo.
Sendo n o número de cestas e C(n) o custo em função do número de cestas produzidas:
Considerando n = 9,
Em um dia de trabalho no qual nove cestas foram produzidas, o custo é de:
R$ 474,00
Exercício 5 (Grandezas diretamente proporcionais e regra de três simples)
Habilidade BNCC EF09MA08
Um caminhão-pipa é um veículo que transporta um reservatório com capacidade para guardar grandes quantidades de líquido. Em uma empresa fornecedora de água, há dois modelos destes veículos. Um motorista que geralmente trabalha com um destes caminhões com capacidade para transportar 3 000 L sabe que, no posto de abastecimento da empresa, o reservatório estará cheio em 12 min.
Este motorista foi escalado para levar outro modelo para abastecer, com capacidade para 8 500 L. No mesmo posto de abastecimento, o tempo necessário para abastecer este modelo será de
a) 34 min
b) 36 min
c) 30 min
d) 24 min
As grandezas envolvidas no problema são: a quantidade de litros e o tempo.
Ao aumentar a capacidade do reservatório, mais tempo será necessário para enchê-lo, sendo as grandezas diretamente proporcionais.
| capacidade em litros | tempo |
|---|---|
| 3000 l | 12 min |
| 8500 l | x |
Montando a proporção,
Para resolver a proporção, multiplicamos os meios pelos extremos (multiplicar cruzado).
Considerando a mesma vazão (quantidade de água por unidade de tempo), pois a estação de abastecimento é a mesma, para abastecer 8500 L serão necessários 34 minutos.
Exercício 6 (Grandezas inversamente proporcionais e regra de três composta)
Habilidade BNCC EF09MA08
Uma empresa que produz camisas recebeu uma encomenda de 7 020 unidades que deve estar pronta para entrega em cinco dias. Atualmente a confecção conta com 18 costureiras que produzem 1080 camisas em um dia de trabalho. Para conseguir atender o pedido, quantas costureiras devem ser contratadas nos próximos cinco dias?
a) 4 costureiras
b) 99 costureiras
c) 6 costureiras
d) 100 costureiras
As grandezas envolvidas na situação são:
Número de costureiras;
Quantidade produzida;Dias de trabalho.Como o número desconhecido está na coluna das costureiras, comparamos esta grandeza com as outras.
Mais costureiras aumentam a produção. Sendo um par de grandezas diretamente proporcionais.
Mais costureiras produzem uma mesma quantidade em menos dias. Sendo um par de grandezas inversamente proporcionais.
Trazendo os dados e organizando na forma de tabela:
| costureiras | produção | dias |
|---|---|---|
| 18 | 1080 | 1 |
| x | 7020 | 5 |
Montando a proporção:
Como a grandeza dias é inversamente proporcional a costureiras, devemos inverter esta razão.
Para solucionar, primeiro multiplicamos as duas frações ao lado direito da igualdade.
Multiplicando cruzado:
Como o próximo número inteiro é 24, deve-se contratar mais 6 costureiras. Pois,
24 - 18 = 6
Exercício 7 (Expressões algébricas: fatoração)
Habilidade BNCC EF09MA09
Fatore as expressões.
a)
b)
c)
Exercício 8 (Expressões algébricas: produtos notáveis)
Habilidade BNCC EF09MA09
Desenvolva os produtos notáveis.
a)
b)
c)
Exercício 9 (Retas paralelas cortadas por uma transversal)
Habilidade BNCC EF09MA10
Na imagem, r e s são retas paralelas e t é uma reta transversal. Determine o valor de x.
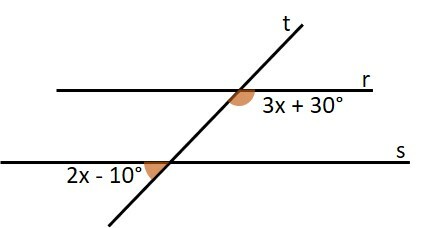
Exercício 10 (Arcos, ângulos centrais e ângulos inscritos na circunferência)
Habilidade BNCC EF09MA11
Determine os ângulos x, y e z referentes à circunferência abaixo.

a) x=60º, y=45º e z=15º
b) x=60º, y=30º e z=22,5º
c) x=45º, y=30º e z=15º
d) x=30º, y=45º e z=60º
x é um ângulo central e seu valor é igual ao do arco que ele determina, 60º.
y é um ângulo inscrito e seu valor é igual à metade do arco que ele determina.
z é um ângulo externo que determina dois arcos, o de 15º e 60º. Seu valor é a metade da diferença entre os dois.
Exercício 11 (Semelhança de triângulos)
Habilidade BNCC EF09MA12
Determine a medida do segmento DE.

a) 2 cm
b) 15 cm
c) 3,75 cm
d) 5,25 cm
O segmento DE pode ser determinado por DC - EC.
Cálculo de DC
O segmento DB está dividindo o retângulo em dois triângulos retângulos de altura 8 cm e hipotenusa 17 cm. Utilizando o teorema de Pitágoras podemos determinar o lado DC.
Cálculo de EC
Os triângulos BCD e FCE são semelhantes pelo caso AAA. Podemos nos utilizar das proporções dos segmentos entre alturas e bases para determinar EC.
Cálculo de DE
Exercício 12 (Relações métricas no triângulo retângulo)
Habilidade BNCC EF09MA13
Na imagem abaixo, as medidas de h, c e b são, respectivamente,
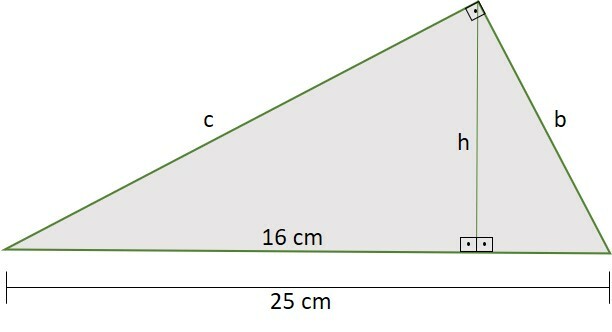
a) h = 20 cm, c = 15 cm e b = 12 cm
b) h = 8 cm, c = 10 cm e b = 5 cm
c) h = 10 cm, c = 5 cm e b = 8 cm
d) h = 12 cm, c = 20 cm e b = 15 cm
A imagem é formada por três triângulos retângulos. Subtraindo da base maior, de 25 cm, os 16 cm, temos que a base do menor triângulo é de 9 cm.
Há algumas relações importantes:
Onde,
a = 25 cm é a base maior;
n = 9 cm é a projeção de b;
m = 16 cm é a projeção de c.
Substituindo os valores, temos:
Cálculo de c.
Cálculo de b.
Cálculo de h.
Exercício 13 (Teorema de Pitágoras)
Habilidade BNCC EF09MA14
Para trocar uma lâmpada em um poste, uma escada de 5 m de comprimento foi utilizada, e uma de suas extremidades ficou apoiada no topo do poste. As bases da escada e do poste ficaram distantes 1 m entre si. Desta forma, a altura do poste é de
a) 4,89 m
b) 5,09 m
c) 3,97 m
d) 4,00 m
A escada de 5 m, o poste e a distância no solo de 1m formam um triângulo retângulo. Para determinar a altura do poste, utilizamos o teorema de Pitágoras.
No triângulo formado, a escada é a hipotenusa, lado oposto ao ângulo de 90º. A distância de 1 m entre a escada e o poste é um cateto e o poste é o outro.
Assim, o poste possui, aproximadamente, 4,89 m de altura.
Exercício 14 (Polígonos regulares)
Habilidade BNCC EF09MA15
As medidas dos ângulos central, interno e externo de um pentágono regular são, respectivamente,
a) Central = 72º, interno = 108º e externo = 72º.
b) Central = 360º, interno = 72º e externo = 252º.
c) Central = 360º, interno = 108º e externo = 72º.
d) Central = 72º, interno = 252º e externo = 72º.
Ângulo central
A partir do centro do pentágono, traçando segmentos até os vértices, formam-se cinco ângulos iguais, que, somados, completam uma volta.
Ângulo externo
O ângulo externo segue o mesmo raciocínio anterior.
Ângulo interno
Para determinar a medida de um ângulo interno, determinamos o total e, depois, dividimos pela quantidade de ângulos.
A soma dos ângulos internos de um polígono regular é dada por:
Sendo n o número de lados do polígono.
Como em um pentágono há 5 ângulos internos, basta dividir 540 por 5.
Exercício 15 (Distância entre pontos no plano cartesiano)
Habilidade BNCC EF09MA16
No plano cartesiano, determine a distância entre os pontos A e B.
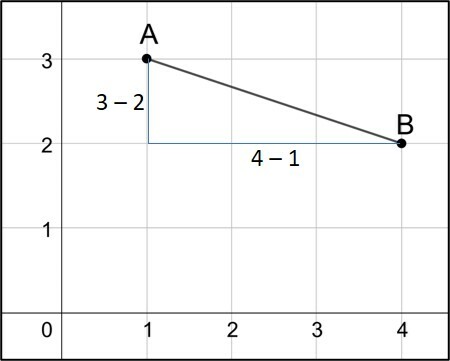
a) 3 unidades
b) unidades
c) 5 unidades
d) unidades
Para determinar o comprimento do segmento AB devemos, antes, determinar os pares ordenados de cada ponto.
A(1, 3), 1 no eixo horizontal x e 3 no eixo vertical y.
B(4,2), 4 no eixo horizontal x e 2 no eixo vertical y.
AB é a hipotenusa de um triângulo retângulo de catetos 1 e 4.

Utilizamos o teorema de Pitágoras:
Exercício 16 (Vistas ortogonais de figuras espaciais)
Habilidade BNCC EF09MA17
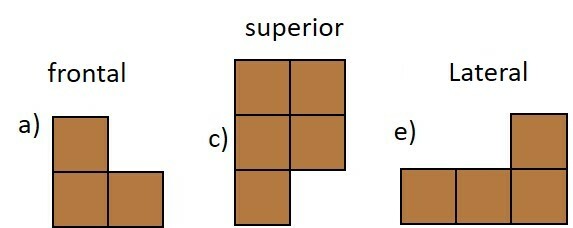
Uma empresa que vende pela internet está encaixotando produtos para entrega. Relacione as vistas ortogonais da pilha de caixas.
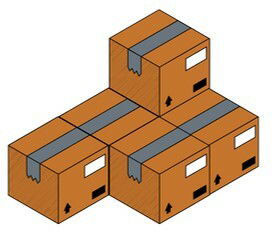
Das opções abaixo, relacione as vistas superior, lateral e frontal das caixas.
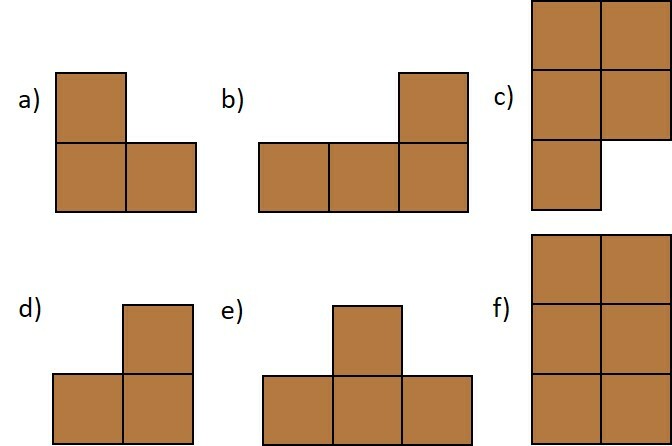
Exercício 17 (Volume e área de prismas)
Habilidade BNCC EF09MA19
Uma caixa de papelão na forma de paralelepípedo reto retângulo está sendo projetada para embalar determinado produto. É preciso conhecer a quantidade de papelão utilizado para a produção de 1 caixa. Uma de suas medidas ainda não foi determinada, mas sabe-se que seu volume deve possuir 1 000 cm³ e que há dois lados cujas medidas são iguais a 5 cm. Desconsiderando dobras, a quantidade de papelão necessária para produzir uma caixa, em cm², é de
a) 900 cm²
b) 40 cm²
c) 425 cm²
d) 850 cm²
Objetivo
Determinar a área total da superfície.
Dados
Forma de um paralelepípedo.
Duas medidas são iguais a 5 cm.
O volume é igual a 1000 cm³.
Resolução
A quantidade de papelão é igual à medida da área total. Para determinar a área, precisamos das três medidas: comprimento, altura e largura.
Passo 1: determinar a medida que está faltando.
Como o volume é calculado pelo produto das três medidas, temos:
Passo 2: calcular a área total.
Um paralelepípedo possui seis faces, duas a duas paralelas e iguais. Como os lados são retângulos, multiplicamos uma medida pela outra, em cada lado.
Ainda, como há dois lados iguais, multiplicamos a área de cada lado por dois.
Exercício 18 (Volume de cilindros)
Habilidade BNCC EF09MA19
Um cilindro possui altura de 1 m e volume igual a 27 m³. A área total da superfície deste cilindro é
Use .
a) 18 m²
b) 64 m²
c) 72 m²
d) 54 m²
A área total da superfície de um cilindro é sua área lateral mais as áreas das bases.
As bases, de baixo e de cima, são duas circunferências, e a área lateral é um retângulo.
Se imaginarmos uma superfície flexível, abrirmos o cilindro ao longo de sua altura e esticá-lo, teremos um retângulo de altura h. O seu comprimento é o mesmo da circunferência.
Assim, a área da superfície total do cilindro é:
A = área da base + área da base + área lateral
A = 2 . área da base + área lateral
Temos o valor de e a altura, fornecidos no enunciado. Precisamos determinar o raio r. Temos a informação de que o volume é igual a 27 m³. Escrevendo a fórmula do volume:
Podemos determinar o raio isolando r na fórmula do volume.
Substituindo os valores na fórmula da área, temos:
Exercício 19 (Probabilidade)
Habilidade BNCC EF09MA20
Em um jogo de tabuleiro, deve-se arremessar dois dados, um amarelo e um azul, onde os números nas faces voltadas para cima são multiplicados. Os jogadores que tiverem como resultado um produto menor ou igual a 16 são eliminados. A probabilidade de se manter no jogo após a primeira rodada é de
a) 73%
b) 22%
c) 10%
d) 27%
Os produtos entres os resultados dos dois dados são:

Dentre os resultados possíveis estão marcados os maiores de 16:
{18, 18, 20, 20, 24, 24, 25, 30, 30, 36}
Estamos considerando que a ordem dos resultados nos dados é diferente. Por exemplo:
Sair 4 no amarelo e 6 no azul, será uma possibilidade diferente de 4 no azul e 6 no amarelo.
São 10 resultados possíveis, favoráveis a continuar no jogo, entre 36 diferentes.
O cálculo da probabilidade é:
Exercício 20 (Gráficos)
Habilidade BNCC EF09MA21
O seguinte gráfico de linhas mostra a evolução do IPCA de 1996 a 2016, com o acumulado de cada ano. O IPCA, Índice de Preços ao Consumidor Amplo, é um índice que mede a inflação de produtos consumidos no Brasil. Na prática, ele indica se os preços aumentaram, diminuíram ou permaneceram estáveis.
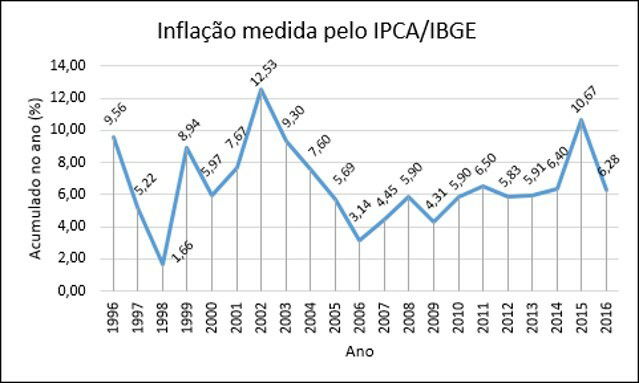
a) Qual foi o ano que apresentou o maior IPCA? Quanto foi seu valor?
b) Entre quais anos ocorreu a maior queda do índice e de quanto foi esta variação?
c) Em qual ano o índice apresentou o valor mais baixo e de quanto foi este valor?
d) Qual foi a variação do índice entre os anos de 2009 e 2011?
Exercício 21 (Pesquisa amostral)
Habilidade BNCC EF09MA23
Em uma disputa nos jogos olímpicos estudantis, uma das modalidades disputada foi o salto a distância. Nove atletas mirins participaram. Por ordem dos saltos, os resultados foram, em metros:
| 1º | 2º | 3º | 4º | 5º | 6º | 7º | 8º | 9º |
| 3,75 | 3,86 | 3,46 | 4,35 | 4,15 | 3,94 | 3,82 | 4,15 | 4,08 |
Em relação aos resultados na prova de salto a distância, a média simples, a moda e a mediana foram, nesta ordem:
a) 3,95 m, 3,94 m e 4,15 m.
b) 3,95 m, 4,15 m e 3,94 m.
c) 3,95 m, 4,35 m e 4,15 m.
d) 3,94 m, 4,15 m e 3,95 m.
Cálculo da média aritmética
Para o cálculo da média aritmética, devemos somar os valores e dividir pela quantidade de saltos, no caso, 9.
A média aritmética foi de, aproximadamente, 3,95 m.
Cálculo da moda
A moda é o valor que mais se repete. Neste caso, o valor 4,15 se repete duas vezes, sendo a moda do conjunto.
Cálculo da mediana
Para o cálculo de mediana, organizamos os dados em ordem crescente, no que chamamos de Rol.
| 3,46 | 3,75 | 3,82 | 3,86 | 3,94 | 4,08 | 4,15 | 4,15 | 4,35 |
A mediana é o valor central do Rol de dados. Como há nove elementos no conjunto, a mediana é o 5º termo, no caso, 3,94.
Veja também:
- Exercícios de Matemática 6º ano
- 27 exercícios de Matemática Básica
- 23 exercícios de Matemática 7º ano
- Exercícios de Matemática 8º ano
ASTH, Rafael. Exercícios de Matemática 9º ano com respostas. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-de-matematica-9-ano/. Acesso em: