Exercícios sobre a soma dos ângulos internos de um polígono
Os polígonos podem ter a soma dos seus ângulos internos determinados por procedimentos simples. Pratique com estes exercícios e acompanhe as resoluções comentadas para tirar suas dúvidas.
Exercício 1
Um arquiteto está projetando uma sala de reuniões com o formato de um polígono regular de 12 lados. Ele precisa calcular a soma dos ângulos internos desse polígono para, assim, determinar a medida de cada ângulo. Qual é a soma dos ângulos internos dessa sala e a medida de cada ângulo em graus?
a) 1440° e 120º.
b) 1620° e 135º.
c) 1800° e 150º.
d) 1980° e 165º.
e) 2160° e 180º.
A soma dos ângulos internos pode ser obtida pela equação:
Para determinar a medida de cada ângulo, basta dividir pelo número de lados, 12.
Conclusão
A soma dos ângulos internos de todos os ângulos é 1800° e, cada ângulo individual, 150º.
Exercício 2
Um polígono possui como soma de todos seus ângulos internos 1260º. Pode-se afirmar que este polígono é um
a) Quadrado
b) Pentágono
c) Octógono
d) Eneágono
e) Decágono
A soma dos ângulos de um polígono é dada por:
Onde n é o número de lados do polígono.
Substituindo o Si por 1260 na equação acima:
Conclusão
Como n=9, o polígono é um eneágono.
Exercício 3
Um engenheiro civil está projetando uma estrutura com o formato de um polígono de 15 lados. Ele precisa saber a soma dos ângulos internos desse polígono para calcular corretamente os ângulos de inclinação das vigas. Qual é a soma dos ângulos internos dessa estrutura em graus?
a) 1980°
b) 2160°
c) 2340°
d) 2520°
e) 2700°
A soma dos ângulos internos de um polígono é dada por:
Onde n é o número de lados.
Substituindo n por 15 na equação acima, temos:
Exercício 4
A medida de um único ângulo interno de um dodecágono regular é
a) 130.
b) 150º.
c) 180º.
d) 210.
e) 225.
Um dodecágono é um polígono com 12 lados. Sendo regular, todos os lados e ângulos são iguais.
Ao dividirmos a soma dos valores dos ângulos internos pelo número de lados, determinamos o valor de um único ângulo.
A soma é obtido por:
Para determinar o valor de um único ângulo, basta dividir por 12.
Conclusão:
O valor de um único ângulo interno de um dodecágono regular é 150º.
Exercício 5
Analise a figura abaixo:
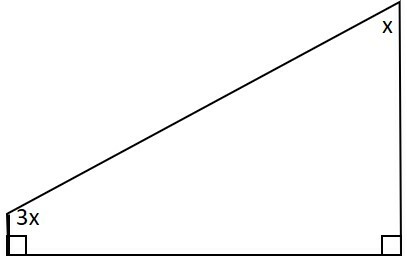
Em ordem crescente, a opção que descreve os ângulos internos no trapézio é
a) 10º, 90º, 90º e 170º.
b) 36º, 90º, 90º e 144º.
c) 72º, 90º, 90º e 108º.
d) 45º, 90º, 90 e 135º.
e) 60º, 90º, 90º e 120º.
O trapézio da figura é retângulo por possuir dois ângulos retos.
Calculemos a soma dos ângulos internos de um polígono com quatro lados.
A figura nos mostra que um ângulo desconhecido é três vezes maior que o outro. Somando os quatro valores:
Assim, o menor ângulo é de 45º, os intermediários são iguais a 90º e o maior, três vezes 45º, possui 135º.
Logo, a resposta correta é a letra d) 45º, 90º, 90º e 135º.
Exercício 6
Suponha um polígono convexo regular que possua seus ângulos externos com medida de 20º. Neste caso, o número de lados deste polígono será
a) 13.
d) 16.
c) 18.
d) 20.
e) 23.
Ideia inicial: o número de lados é igual ao número de ângulos.
Passo 1: determinar o ângulo interno.
Sabemos que um ângulo externo somado ao interno resulta em 180º, o que nos possibilita descobrir o valor de seu ângulo interno.
180–20 = 160
Logo, como o polígono é regular, todos seus ângulos internos são iguais.
Passo 2: escrever a relação entre ângulo interno e a soma dos ângulos internos deste polígono.
Um ângulo interno em um polígono regular é determinado ao dividir a soma de todos pelo número de lados.
Onde:
é a medida do ângulo interno;
é a soma das medidas de todos os ângulos internos;
n é o número de lados.
Passo 3: utilizar a fórmula dos ângulos internos de um polígono e resolver a equação para n.
Substituindo o valor de :
Abrindo a fórmula :
Resolvendo para n:
Conclusão
O número de lados do polígono é 18.
Aprenda mais sobre o tema com:
Para mais exercícios sobre ângulos e polígonos:
- Exercícios sobre ângulos (com questões respondidas)
- Exercícios sobre polígonos (com gabarito explicado)
ASTH, Rafael. Exercícios sobre a soma dos ângulos internos de um polígono. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-a-soma-dos-angulos-internos-de-um-poligono/. Acesso em:


