Exercícios sobre ângulos (com questões respondidas)
Pratique seu conhecimento sobre ângulos com nossos exercícios resolvidos e explicados. Aprenda de vez como classificar, medir e utilizar os ângulos para resolver problemas escolares e reais.
Exercício 1
Qual opção fornece um par de ângulos complementar um ao outro?
a) 40º e 20º
b) 60º e 40º
c) 75º e 15º
d) 120º e 60º
e) 300º e 60º
Ângulos complementares são aqueles que somados resultam em 90º. Assim,
75º + 15º = 90º
Exercício 2
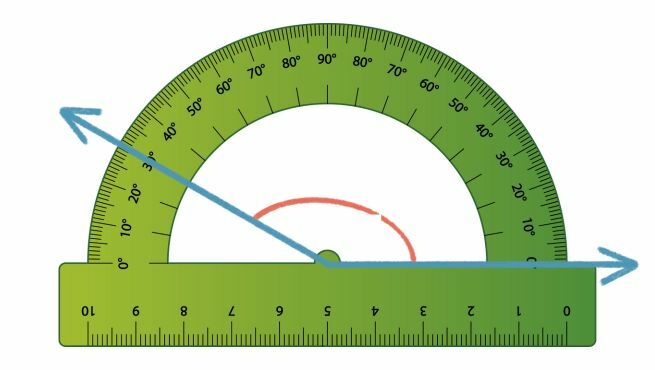
Classifique o ângulo abaixo de acordo com sua medida:
a) Agudo
b) Reto
c) Obtuso
d) Raso
e) Não é possível determinar apenas pela figura
Os ângulos obtusos são maiores que 90º.
Na imagem temos um ângulo de 150º.
90º + (90º - 30º) = 90º + 60º = 150º
Exercício 3
Sabendo que dois ângulos x e y são suplementares e, que o ângulo x possui 36º, a medida do ângulo y é igual a
a) 24º.
b) 54º.
c) 64º.
d) 144º.
e) 324º.
Dois ângulos são suplementares quando somam 180º. Assim:
36º + 144º = 180º
Exercício 4
Na imagem abaixo as retas são concorrentes no ponto O. Com respeito aos ângulos formados, podemos afirmar que
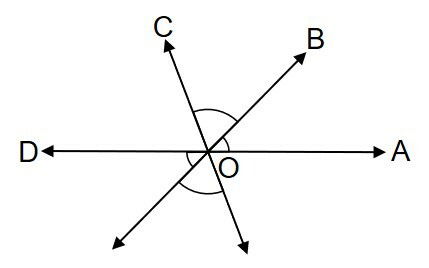
a) AÔB e BÔC são suplementares.
b) AÔB e BÔC são opostos pelo vértice.
c) AÔB e CÔD são adjacentes.
d) BÔC e CÔD são consecutivos.
e) DÔC e BÔA são opostos pelo vértice.
Exercício 5
Observe a imagem do transferidor onde estão determinados os ângulos A, P, V, L e R.
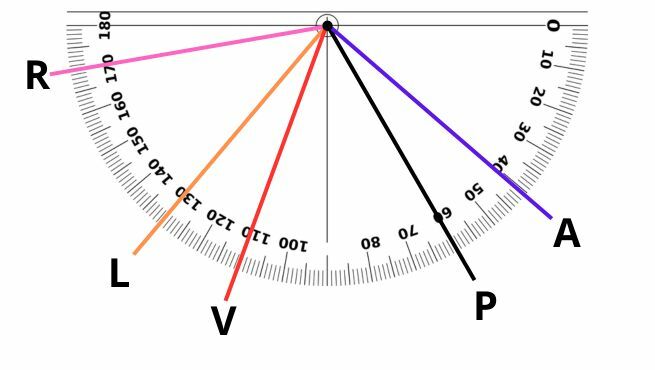
Marque a opção que fornece o resultado da seguinte expressão:
a) 3A + 2P - L = 100º
b) P - A + V - L = 10º
c) 2V - 3A = 70º
d) R - L - (L-V) = 20º
e) R + 2A = 360º
R - L - (L-V) = 20º
170 - 130 - (130 - 110) =
40 - 20 =
20
Exercício 6
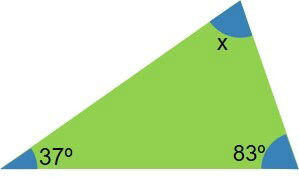
Um triângulo é um polígono com três lados e três ângulos. Sabendo que ao somar os três ângulos de qualquer triângulo o resultado é sempre o ângulo raso, no triângulo abaixo o ângulo que está faltando é de
a) 29º.
b) 40º.
c) 47º.
d) 53º.
e) 60º
Ângulo raso é um ângulo de 180º, ou meia volta.
Como os três ângulos somados devem ser iguais a 180º, basta terminar quantos graus faltam para 180º no terceiro ângulo, o ângulo x.
37 + 83 = 120
Assim, para 180 faltam:
180 - 120 = 60
Exercício 7
Sendo o ângulo AÔC reto, os ângulos AÔB e BÔC valem, respectivamente

a) 20° e 70º.
b) 30° e 60º
c) 40° e 50º
d) 50° e 40º.
e) 60º e 30°.
Passo 1: determinar o valor de x.
Passo 2: determinar o valor dos ângulos.
AÔB = x + 50
AÔB = 10 + 50
AÔB = 60º
Para o ângulo BÔC, basta verificar quantos graus faltam para completar 90º, no caso:
90 - 60 = 30
BÔC = 30º
Exercício 8
Paulo é um estudante curioso e observador. Ele estava analisando o movimento dos ponteiros de um relógio analógico e ficou intrigado com os ângulos formados entre eles em diferentes horários. Paulo percebeu que ao longo do dia, os ponteiros do relógio se movem e formam ângulos distintos, indicando diferentes horas. Ele decidiu investigar esses ângulos para aprimorar seus conhecimentos matemáticos.
Qual é o ângulo formado pelos ponteiros do relógio quando ele marca 6 h e 30 min?
a) 5°
b) 15°
c) 30°
d) 60°
e) 120°
Um relógio de ponteiros possui marcações a cada 5 min, dividindo uma circunferência em 12 partes iguais.
Como uma circunferência possui 360°, cada parte de 5 min possui:
360° / 12 = 30°
Às 6 h e 30 min, o ponteiro dos minutos está exatamente no meio da circunferência. Enquanto este ponteiro percorreu a metade da circunferência a partir das 6 h, o ponteiro das horas também se moveu.
Em meia hora, ou trinta minutos, o ponteiro das horas percorreu a metade do caminho entre 6h e 7h.
Como a passagem entre às 6h e 7h possui 30° e, o ponteiro das horas está na metade deste percurso, o ângulo entre eles é de 15°.
Exercício 9
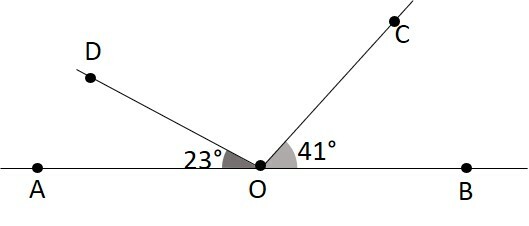
Na imagem abaixo, AÔB é um ângulo raso, assim, o ângulo DÔC possui
64°
90°
100º
116°
141°
Um ângulo raso possui 180°. Retirando 23° e 41°:
180° - 23° - 41° = 116°.
Exercício 10
Um pentágono é um polígono com cinco lados. Na malha triangular abaixo, um pentágono foi destacado, como mostra a imagem.
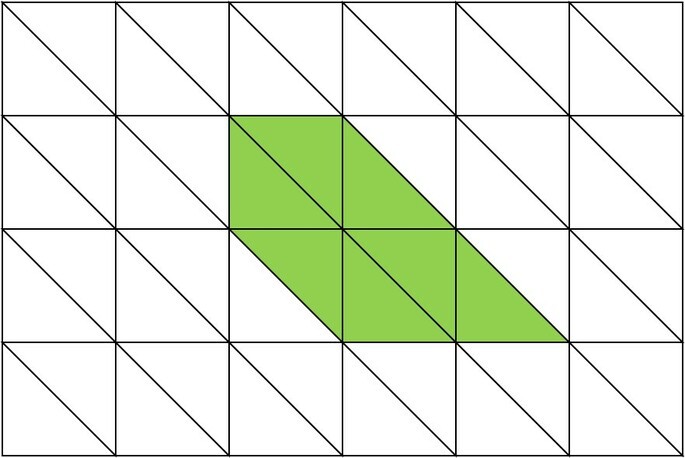
Cada triângulo nesta imagem é retângulo, ou seja, possui um ângulo reto. Como também são isósceles, os outros dois ângulos são iguais a 45° cada.
Observando a imagem, é possível concluir que a soma dos ângulos internos deste pentágono é de
a) 180º
b) 360°
c) 450°
d) 540°
e) 675°
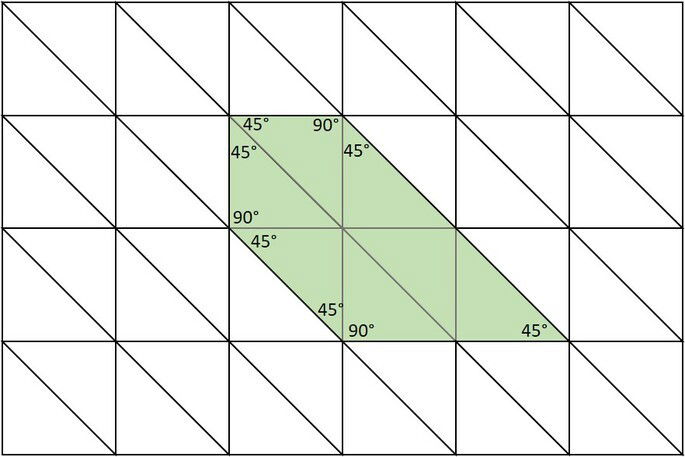
Marcando na imagem os ângulos de 90° e 45°, podemos somá-los:
Aprenda mais sobre ângulos em:
- Ângulos: definição, tipos, como medir e exercícios
- Ângulos Complementares: como calcular e exercícios
- Exercícios sobre retas paralelas cortadas por uma transversal
- Exercícios sobre triângulos (com respostas explicadas)
- Exercícios sobre a soma dos ângulos internos de um polígono
Você pode se interessar por:
Caso queira mais atividades e exercícios de matemática para o sexto ano:
ASTH, Rafael. Exercícios sobre ângulos (com questões respondidas). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-angulos/. Acesso em:


