Exercícios sobre área de retângulos (respostas explicadas)

Rafael C. Asth

Professor de Matemática e Física

Para treinar exercícios sobre área do retângulo, estude com os que preparamos para você, todos com respostas explicadas.

O retângulo é um polígono, uma figura plana e fechada, formada por segmentos de reta. Recorrente nas aulas de matemática e em aplicações no mundo real, é importante compreender bem suas propriedades, como o cálculo de sua área.

Questão 1

Calcule a área de um retângulo que possui uma base de 6 metros e uma altura de 4 metros.

Ver Resposta

Resposta correta: 24 m²

A área de um retângulo é determinada pelo produto entre a medida de sua base e sua altura.

$reto A igual a reto b espaço. espaço reto h$

Onde,

A é a área,
b é a medida da base,
h é a medida da altura.

$reto A igual a reto b espaço. espaço reto h reto A igual a 6 espaço reto m espaço sinal de multiplicação espaço 4 espaço reto m reto A espaço igual a espaço 6 espaço sinal de multiplicação espaço 4 espaço reto m espaço sinal de multiplicação espaço reto m reto A espaço igual a espaço 24 espaço reto m ao quadrado$

Questão 2

Um retângulo possui área de 204 metros quadrados e um dos lados mede 12 metros. Qual é a medida do outro lado?

Ver Resposta

Resposta correta: 17 metros.

A área do retângulo é dada por:

$reto A igual a reto b espaço. espaço reto h$

Como o enunciado não especifica qual lado mede 12 metros, podemos utilizar qualquer um, b ou h.

$reto A espaço igual a espaço reto b espaço. espaço reto h 204 espaço igual a espaço 12 espaço. espaço reto h numerador 204 espaço sobre denominador 12 fim da fração igual a reto h 17 espaço igual a espaço reto h$

Questão 3

Um retângulo possui área de 1200 metros quadrados. Se a razão entre a largura e o comprimento do retângulo é de $1 terço$ , qual é a medida do comprimento e da largura do retângulo?

Ver Resposta

Resposta correta: 60 metros de comprimento e 20 metros de largura.

A área do retângulo é calculada por pela multiplicação da medida se sua base pela altura ou, comprimento pela largura.

Sendo l a largura e c o comprimento, temos:

$reto A igual a reto l espaço. espaço reto c 1200 igual a reto l espaço. espaço reto c$

O enunciado também diz que a razão entre a largura e comprimento é de 1/3.

$reto l sobre reto c igual a 1 terço$

Podemos isolar uma medida desconhecida e substituir na equação da área.

$reto l sobre reto c igual a 1 terço reto l igual a reto c sobre 3$

Substituindo na equação da área:

$1200 igual a reto l espaço. espaço reto l sobre 3 1200 espaço. espaço 3 espaço igual a espaço reto l espaço. espaço reto l 3600 espaço igual a espaço reto l ao quadrado raiz quadrada de 3600 igual a reto l 60 espaço igual a espaço reto l$

Para o comprimento:

$reto A igual a reto l espaço. espaço reto c 1200 espaço igual a espaço 60 espaço. espaço reto c 1200 sobre 60 igual a reto c 20 espaço igual a espaço reto c$

Questão 4

Uma sala retangular possui as seguintes dimensões: largura de 6 metros e comprimento de 4,8 metros. Você decidiu realizar uma reforma na sala, onde será instalado um piso quadrado em todo o chão.

Os pisos quadrados disponíveis para instalação têm medidas de lado de 0,6 metros. Quantos pisos quadrados serão necessários para cobrir todo o chão da sala, considerando que não haverá cortes nos pisos?

Ver Resposta

Resposta correta: 80 pisos

Área da sala:

$reto A igual a 6 espaço sinal de multiplicação espaço 4 vírgula 8 reto A igual a 28 vírgula 8 espaço reto m ao quadrado$

Área de cada piso:

$reto A igual a 0 vírgula 6 espaço sinal de multiplicação espaço 0 vírgula 6 reto A igual a 0 vírgula 36 espaço reto m ao quadrado$

Dividindo a área da sala pela área de cada piso:

$n º espaço d e espaço p i s o s espaço igual a espaço numerador á r e a espaço d a espaço s a l a sobre denominador á r e a espaço d o espaço p i s o fim da fração n º espaço d e espaço p i s o s espaço igual a espaço numerador 28 vírgula 8 sobre denominador 0 vírgula 36 fim da fração n º espaço d e espaço p i s o s espaço igual a espaço 80$

Questão 5

Um retângulo possui suas medidas na seguinte forma: a base mede (x - 5) e a altura (x - 3). Sabe-se que o valor de sua área deve ser de 3 m². Sendo assim, quais são os possíveis valores de x?

Ver Resposta

Resposta correta: 2 e 6 metros.

Como a área de um retângulo é determinada pelo produto de seus lados e, a área deste retângulo é igual a 3 m², fazemos:

$parêntese esquerdo x menos 5 parêntese direito. parêntese esquerdo x menos 3 parêntese direito igual a 3 x ao quadrado menos 3 x espaço menos 5 x espaço mais espaço 15 igual a 3 x ao quadrado menos 8 x mais 15 igual a 3 x ao quadrado menos 8 x mais 12 igual a 0$

Resolvendo a equação do segundo grau:

$incremento igual a b ao quadrado menos 4. a. c incremento igual a parêntese esquerdo menos 8 parêntese direito ao quadrado menos 4.1.12 incremento igual a 64 menos 48 incremento igual a 16$

Calculando as raízes:

$reto x com 1 subscrito igual a numerador menos reto b mais raiz quadrada de incremento sobre denominador 2. reto a fim da fração igual a numerador menos parêntese esquerdo menos 8 parêntese direito mais raiz quadrada de 16 sobre denominador 2.1 fim da fração igual a numerador 8 mais 4 sobre denominador 2 fim da fração igual a 12 sobre 2 igual a 6 reto e reto x com 2 subscrito igual a numerador menos reto b menos raiz quadrada de incremento sobre denominador 2. reto a fim da fração igual a numerador menos parêntese esquerdo menos 8 parêntese direito menos raiz quadrada de 16 sobre denominador 2.1 fim da fração igual a numerador 8 menos 4 sobre denominador 2 fim da fração igual a 4 sobre 2 igual a 2$

Conferindo

Sendo x = 6m:

$parêntese esquerdo x menos 5 parêntese direito. parêntese esquerdo x menos 3 parêntese direito igual a parêntese esquerdo 6 menos 5 parêntese direito. parêntese esquerdo 6 menos 3 parêntese direito igual a 1 espaço. espaço 3 espaço igual a 3$

Sendo x = 2m:

$parêntese esquerdo x menos 5 parêntese direito. parêntese esquerdo x menos 3 parêntese direito igual a parêntese esquerdo 2 menos 5 parêntese direito. parêntese esquerdo 2 menos 3 parêntese direito igual a menos 3 espaço. espaço parêntese esquerdo menos 1 parêntese direito igual a 3$

Questão 6

Uma piscina em forma de paralelepípedo tem comprimento de 9 m, largura de 7 m e profundidade de 2 m. Um revestimento será aplicado em todas as superfícies que compõem a piscina, sendo necessário conhecer sua área total.

Este valor em metros quadrados será:

Ver Resposta

Resposta correta: 127 m²

Área do fundo

O fundo da piscina é um retângulo de lados 9 e 7 m.

A = 9 . 7 = 63 m²

Área de um par de lados paralelos

Como a piscina tem a forma de um paralelepípedo, há dois pares de lados paralelos.

A = 9 . 2 = 18 m²

Assim, o par terá 18 . 2 = 36 m².

Área do outro par de lados paralelos:

A = 7 . 2 = 14 m²

Assim, o par terá 28 m²

Somando, temos:

Área total = 63 + 36 + 28 = 127 m²

Questão 7

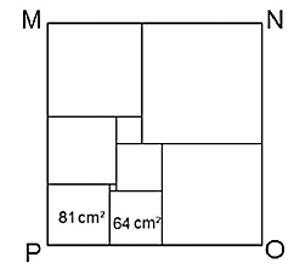
(Esamc 2015) A figura a seguir apresenta um quadrilátero MNOP que foi dividido em 9 quadrados menores. As áreas de dois desses quadrados (64 cm² e 81 cm²) estão indicadas na figura. Nessas condições, a área do quadrilátero MNOP é igual a:

a) 1056 cm²

b) 1024 cm²

c) 992 cm²

d) 960 cm²

e) 928 cm²

Questão 8

(UFRGS 2016) Na figura abaixo, três discos P, Q e R, de mesmo raio, são construídos de maneira que P e R são tangentes entre si e o centro de Q é ponto de tangência entre P e R. O quadrilátero sombreado ABCD têm vértices nos centros dos discos P e R e em dois pontos de interseção de Q com P e R.

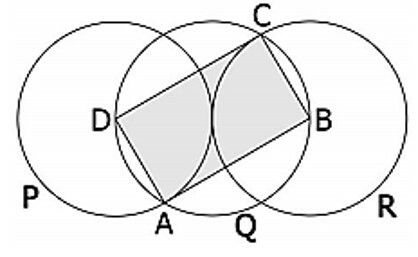
Se o raio do disco P é 5, a área do quadrilátero ABCD é

a) 5√3.

b) 25.

c) 50.

d) 25√3.

e) 75.

Para mais exercícios:

Veja também retângulo : tudo sobre este polígono.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.