Exercícios de circunferência e círculo com respostas explicadas
Os exercícios sobre circunferência e círculo sempre estão em avaliações e vestibulares. Pratique com esta lista de exercícios e tire suas dúvidas com as resoluções explicadas passo a passo.
Questão 1
Para organizar o fluxo de veículos no trânsito, muitas vezes os engenheiros e projetistas utilizam rotatórias ao invés de semáforos, solução que pode ser mais eficiente em muitos casos. Em uma rotatória, o segmento que liga o meio da pista em dois extremos é de 100 m. Um motorista que completar uma volta percorrerá
Dados: utilize =3.
a) 100 m.
b) 150 m.
c) 300 m.
d) 200 m.
O segmento que liga o meio da pista em dois extremos é o diâmetro da rotatória.
Para calcular o comprimento da rotatória, utilizamos:
Onde,
C é o comprimento,
r é o raio
Como o diâmetro é igual a duas vezes o raio, temos:
Assim, o comprimento será:
Em uma volta completa, o motorista irá percorrer 300 metros.
Questão 2
Disco de freio é uma peça circular de metal que faz parte do sistema de frenagem de um veículo. Ele tem a função de retardar ou parar a rotação das rodas.

Para fabricar um lote de 500 discos de freio com 20 cm de diâmetro e uma área central vazia para acoplar o cubo de roda, de 12 cm de diâmetro, um fabricante utilizará, em metros quadrados, um total de chapa metálica de cerca de:
Dados: utilize .
a) 1 m.
b) 10 m.
c) 100 m
d) 1 000
Podemos calcular a área maior e diminuir a central.
A área de um círculo é calculada por:
Área maior
Como o diâmetro é igual a 20 cm, o raio é 10 cm. Em metros, 0,1 m.
Área central
Área do disco = área maior - área menor
Área do disco =
Como são 500 discos:
Substituindo pelo valor de 3,14 informado no enunciado:
Questão 3
Um parque de diversões está construindo uma roda gigante com 22 metros de diâmetro. Uma estrutura de aço na forma de circunferência está sendo construída para fixar os assentos. Se cada assento está a 2 m de distância do próximo e considerando = 3, o número máximo de pessoas que poderão brincar de uma só vez neste brinquedo é
a) 33.
b) 44.
c) 55.
d) 66.
Primeiro devemos calcular o comprimento da circunferência.
Como os assentos estão espaçados por 2 m, temos:
66 / 2 = 33 assentos
Questão 4
Uma bicicleta está equipada com rodas de 26 polegadas, medida do diâmetro. A distância percorrida em metros após dez giros completos das rodas é de
1 polegada = 2,54 cm
a) 6,60 m
b) 19,81 m
c) 33,02 m
d) 78,04 m
Para calcular um giro completo em polegadas, fazemos:
Em centímetros:
C = 78 . 2,54 = 198,12 cm
Em metros:
C = 1,9812 m
Em dez voltas
19,81 m
Questão 5
Um clube está construindo um quiosque circular de 10 m de diâmetro para atender os clientes que chegam de todas as direções. Os dutos e encanamentos já foram instalados, agora uma base com 10 cm de espessura de concreto será construída. Quantos metros cúbicos de concreto serão necessários para preencher esta área?
Considere .
a) 3,10 m³
b) 4,30 m³
c) 7,85 m³
d) 12,26 m³
Calcular quantos metros cúbicos serão necessários, é calcular o volume da base.
Dados:
- Diâmetro de 10 m, portanto, raio de 5 m.
- Espessura de 10 cm = 0,1 m.
Para o cálculo do volume, determinamos a área e multiplicamos pela altura, no caso 10 cm.
Multiplicando pela altura de 10 cm ou 0,1 m:
Substituindo por 3,14:
Questão 6
O Planeta Terra possui um raio aproximado de 6 378 km. Suponha que um navio esteja em trajetória retilínea se deslocando no Oceano Pacífico entre os pontos B e C.

Tomando a Terra como uma circunferência perfeita, considere que o deslocamento angular do navio foi de 30º. Nestas condições e considerando = 3, a distância em quilômetros percorrida pelo navio foi de
a) 1 557 km
b) 2 364 km
c) 2 928 km
d) 3 189 km
1 volta completa = 360º
Com um raio de 6 378 km, o comprimento da circunferência é de:
Fazendo uma regra de três:
Questão 7
(Enem 2016) No projeto de arborização de uma praça está prevista a construção de um canteiro circular. Esse canteiro será constituído de uma área central e de uma faixa circular ao seu redor, conforme ilustra a figura.
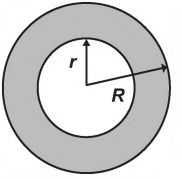
Deseja-se que a área central seja igual à área da faixa circular sombreada.
A relação entre os raios do canteiro (R) e da área central (r) deverá ser
a) R = 2r
b) R = r√2
c)
d)
e)
Área central
Área da faixa circular
Como a área central deve ser igual à área circular sombreada:
Questão 8
A figura representa um círculo λ de centro C. Os pontos A e B pertencem à circunferência de λ e o ponto P pertence a . Sabe-se que PC = PA = k e que PB = 5, em unidades de comprimento.
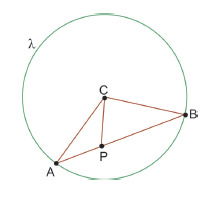
A área de λ, em unidades de área, é igual a
a) π(25 - k²)
b) π(k² + 5k)
c) π(k² + 5)
d) π(5k² + k)
e) π(5k² + 5)
Dados
- CA = CB = raio
- PC = PA = k
- PB = 5
Objetivo: calcular a área circular.
A área circular é , onde o raio é o segmento CA ou CB.
Como as respostas estão em função de k, devemos escrever o raio em função de k.
Resolução
Podemos identificar dois triângulos isósceles.
Como PC = PA, o triângulo é isósceles e, os ângulos da base
e
, são iguais.
Como CA = CB, o triângulo é isósceles e, os ângulos da base
e
, são iguais.
Assim, os dois triângulos são semelhantes devido o caso AA (ângulo-ângulo).
Escrevendo a proporção entre as razões dois lados semelhantes, , temos:
Como queremos a área circular:
Questão 9
(UNICAMP-2021) A figura abaixo exibe três círculos tangentes dois a dois e os três tangentes a uma mesma reta. Os raios dos círculos maiores têm comprimento R e o círculo menor tem raio de comprimento r.
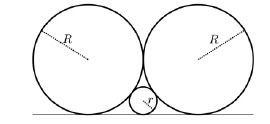
A razão R/r é igual a
3.
√10.
4.
2√5.
Ajustando os raios formamos um triângulo retângulo de hipotenusa R+r e catetos R e R - r.
Aplicando o Teorema de Pitágoras:
Questão 10 (geometria analítica)
(Enem) Considere que os quarteirões de um bairro tenham sido desenhados no sistema cartesiano, sendo a origem o cruzamento das duas ruas mais movimentadas desse bairro. Nesse desenho, as ruas têm suas larguras desconsideradas e todos os quarteirões são quadrados de mesma área e a medida de seu lado é a unidade do sistema.
A seguir há uma representação dessa situação, em que os pontos A, B, C e D representam estabelecimentos comerciais desse bairro.
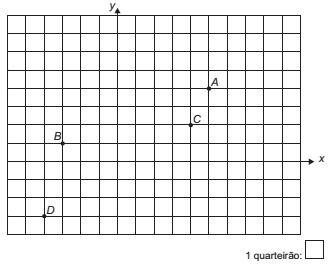
Suponha que uma rádio comunitária, de fraco sinal, garante área de cobertura para todo estabelecimento que se encontre num ponto cujas coordenadas satisfaçam à inequação: x² + y² – 2x – 4y - 31 ≤ 0
A fim de avaliar a qualidade do sinal, e proporcionar uma futura melhora, a assistência técnica da rádio realizou uma inspeção para saber quais estabelecimentos estavam dentro da área de cobertura, pois estes conseguem ouvir a rádio enquanto os outros não.
a) A e C.
b) B e C.
c) B e D.
d) A, B e C.
e) B, C e D.
A equação da circunferência é:
A equação do problema é:
O centro de uma circunferência é o ponto C(a, b). Para determinarmos as coordenadas, igualamos os coeficientes dos termos semelhantes.
Para os termos em x:
Para os termos em y:
O centro da circunferência é o ponto C(1, 2)
Para determinar o raio igualamos os termos livres de x e y:
O sinal da rádio irá atender os estabelecimentos na área da circunferência de centro C(1, 2) e raio menor ou igual a 6. Marcando o desenho no plano:
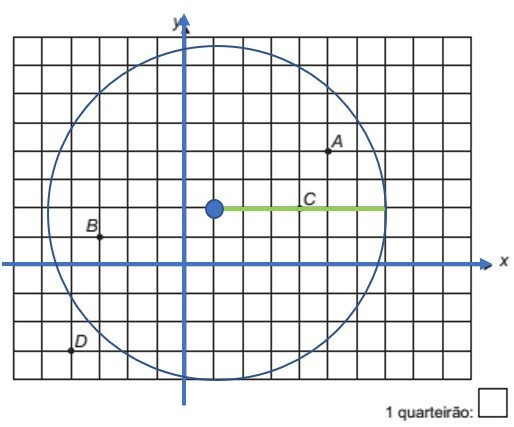
Os estabelecimentos A, B e C receberão o sinal da rádio.
Questão 11
Aprenda mais sobre circunferência em
- O que é Circunferência?
- Comprimento da Circunferência
- Como Calcular a Área do Círculo?
- Área do setor circular
- Número PI (π): valor, origem, como calcular e para que serve
Pratique mais com este Índice de exercícios de matemática do 1º ano do Ensino Médio.
ASTH, Rafael. Exercícios de circunferência e círculo com respostas explicadas. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-circunferencia/. Acesso em:


