Exercícios sobre domínio, contradomínio e imagem (com respostas explicadas)
A compreensão do domínio, do contradomínio e imagem no é fundamental para o estudo das funções. Pratique com a lista de exercícios com respostas comentadas.
Questão 1
Considere a definição de uma função f como uma regra que associa cada elemento do conjunto A a um único elemento do conjunto B. Sobre as definições de domínio, contradomínio e imagem de uma função, analise as alternativas a seguir e assinale a correta:
a) O domínio de uma função é o conjunto de todos os valores possíveis que a variável dependente y pode assumir.
b) O contradomínio de uma função é o conjunto de todos os valores possíveis que a variável independente x pode assumir.
c) A imagem de uma função é o conjunto de todos os valores que y pode assumir a partir dos elementos de x no domínio.
d) O domínio de uma função f é sempre maior que sua imagem.
e) A imagem de uma função é o conjunto de todos os valores que podem ser relacionados à variável independente x.
O domínio de uma função é o conjunto de todos os valores possíveis que a variável independente x pode assumir (alternativa incorreta na letra a).
O contradomínio é o conjunto de todos os valores possíveis que y pode assumir, mas isso não significa que todos os valores serão de fato assumidos (alternativa incorreta na letra b).
A imagem é o subconjunto do contradomínio formado pelos valores que y efetivamente assume, a partir dos valores de x no domínio (alternativa correta na letra c).
O domínio e a imagem de uma função podem ser iguais, dependendo da função (alternativa incorreta na letra d).
A imagem está relacionada aos valores de y, não de x (alternativa incorreta na letra e).
Questão 2
Dado os conjuntos A={0,2,4,6} e B={0,4,8,16,24,36}, determine o domínio, o contradomínio e o conjunto imagem da função f, definida pela correspondência y=x², com x ∈ A e y ∈ B.
A) O domínio de f é {0,2,4,6}, o contradomínio é {0,4,8,16,24,36} e a imagem é {0,4,16,36}.
B) O domínio de f é {0,4,16,36}, o contradomínio é {0,4,8,16,24,36} e a imagem é {0,2,4,6}.
C) O domínio de f é {0,2,4,6} o contradomínio é {0,4,16,36} e a imagem é {0,4,16}.
D) O domínio de f é {0,2,4,6}, o contradomínio é {0,4,8,24} e a imagem é {0,4,36}.
E) O domínio de f é {0,2,4,6}, o contradomínio é {0,4,8,16,36} e a imagem é {0,4,24,36}.
Para auxiliar a visualização, coloquemos os valores em uma tabela:
| x | x² | y |
|---|---|---|
| 0 | 0 | 0 |
| 2 | 4 | 4 |
| 4 | 16 | 16 |
| 6 | 36 | 36 |
x é a variável independente e seus valores pertencem ao conjunto A, por isso, A é o domínio.
y possui seus elementos no conjunto B, sendo o contradomínio.
A imagem são os valores de y associados pela lei da função, y=x².
Questão 3
Considere a função f:R→R definida por .
Analise as seguintes afirmativas:
I. O domínio de f(x) é o conjunto dos números reais, exceto x=2.
II. O contradomínio de f(x) é o conjunto dos números reais R.
III. A imagem de f(x) é o conjunto dos números reais, exceto y=0.
Com base nas afirmativas, qual a alternativa correta?
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Somente as afirmativas I e III são verdadeiras.
E) Todas as afirmativas são verdadeiras.
Domínio: A função está definida para todos os valores de x, exceto x=2, pois para x=2, o denominador se anula e a função não existe. Logo, o domínio é R−{2}.
Contradomínio: O contradomínio foi definido como R, mas a função nunca atinge y=0 (não há valor de x que faça f(x)=0). Portanto, o contradomínio não é R, mas sim R−{0}, tornando a afirmativa II falsa.
Imagem: A imagem da função é o conjunto dos números reais, exceto y=0, pois a função nunca atinge o valor zero.
Questão 4
Considere a função f:R→R definida por .
Analise as seguintes afirmativas:
I. O domínio de f(x) é o conjunto dos números reais R.
II. O contradomínio de f(x) é o conjunto dos números reais.
III. A imagem de f(x) é o conjunto [−4,∞).
Com base nas afirmativas acima, qual a alternativa correta?
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Somente as afirmativas I e II são verdadeiras.
E) Todas as afirmativas são verdadeiras.
Domínio: Como é uma função quadrática, ela está definida para todos os números reais. Logo, o domínio é R.
Contradomínio: O contradomínio é o conjunto dos números reais R, pois a função foi definida assim na questão.
Imagem: A função tem imagem [−4,∞), pois o valor mínimo de f(x) ocorre quando x=0, e f(0)=−4, logo, os valores da função são sempre maiores ou iguais a -4.
Questão 5
Seja a função quadrática , definida com domínio R e contradomínio R. A quantidade de números naturais do domínio (considere o zero), que apresentam imagens positivas nessa função é igual a:
Considere .
A) 10.
B) 8.
C) 7.
D) 9.
E) 6.
Devemos considerar o domínio e o contradomínio sendo o conjunto dos números reais.
O objetivo é determinar os valores de x que pertençam ao domínio que, quando naturais, transformados pela função, produzam h(x) > 0.
Uma função quadrática é determinada pela fórmula: .
O coeficiente a < 0 determina a parábola com concavidade para baixo. Já o parâmetro c = 18, que a parábola corta o eixo y na ordenada 18.
Acompanhe o gráfico:
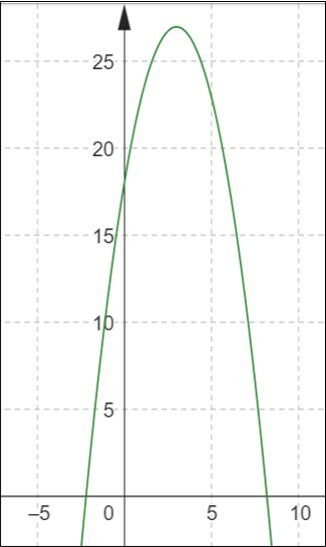
Assim, cogitamos obter os valores naturais de x que vão do zero até o natural mais próximo da raiz.
Para determinar a raiz, utilizamos a fórmula de bhaskara.
Para as raízes:
Como a primeira raiz, x1, é menor que zero, vamos desconsiderá-la. Desta forma, o conjunto dos números naturais que produzem imagens positivas são:
{0, 1, 2, 3, 4, 5, 6, 7, 8}
Portanto, 9 números naturais produzem imagens positivas.
Questão 6
Seja a função f:A→V, dada pela lei . Determine o domínio A que torne f uma função real.
A) A=R-{−2}
B) A=R-{3}
C) A=R-{−3}
D) A=R-{−2,3}
E) A=R-{2}
O domínio da função são os valores de x que a tornem real. Como há um denominador com o termo x + 2, este não pode ser igual a zero, pois não há divisão por zero.
Assim:
Desta forma, o domínio da função são os números reais, exceto o −2.
A=R-{−2}
Questão 7
A seguinte figura representa uma função quadrática real.
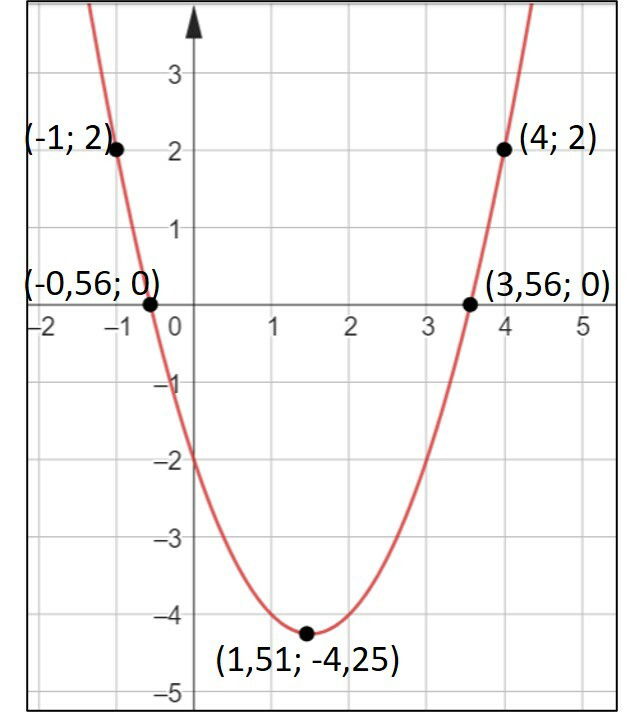
Com base na figura e na definição de função quadrática, o domínio, contradomínio e a imagem são, respectivamente,
a) D= [-0,56; 3,56], CD=[-4,25; 2] e Im=(-;
)
b) D= [-1, 2], CD=() e Im=[-4,25;
)
c) D= [], CD= [
], Im=
d) D= , CD=
; Im= [-4,25;
)
e) CD= [-1; 4], CD=[-0,56; 3,56] e Im= [-4,25; )
Uma função quadrática é da forma , com a, b e c sendo coeficientes reais.
Não há nenhuma restrição para o domínio, sendo o domínio o conjunto dos números reais.
()
O contradomínio também são os números reais.
()
No entanto, a função só possui valores no eixo y acima do seu ponto de mínimo: (1,51, -4,25). Desta forma, a imagem é:
. ou
Questão 8
Aprofunde seus conhecimentos sobre domínio, contradomínio e imagem.
Aprenda mais sobre funções matemáticas:
- Função Injetora
- Função Sobrejetora
- Função Bijetora
- Função Inversa
- Função Composta
- Função par e função ímpar
- Exercícios de Função Afim (Função do 1º Grau)
Referências Bibliográficas
IEZZI, Gelson; BIANCINI, Edwaldo; DOLCE, Osvaldo; FERNANDES, Samuel. Fundamentos da Matemática Elementar - Volume 1: Conjuntos e Funções. 11. ed. São Paulo: Editora Atual, 2015.
ASTH, Rafael. Exercícios sobre domínio, contradomínio e imagem (com respostas explicadas). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-dominio-contradominio-e-imagem/. Acesso em:


