Exercícios sobre funções trigonométricas (com respostas explicadas)
Pratique funções trigonométricas com os exercícios que preparamos para você aprimorar seus conhecimentos e habilidades nessa importante área da matemática.
Questão 1
Uma função periódica se repete ao longo do eixo x. No gráfico abaixo temos a representação de uma função do tipo . O produto A .
é:

a) 2
b) 6
c) .
d) 4.
A amplitude é o módulo da medida entre a linha de equilíbrio (y = 0), e uma crista (ponto mais alto) ou vale (ponto mais baixo).
Assim, A = 2.
O período é o comprimento em x de uma onda completa, que no gráfico, é .
O coeficiente de x pode ser obtido da relação:
O produto entre A e é:
Questão 2
A função real definida por tem período 3
e imagem [-5,5]. A lei da função é
a) f(x) = 5.sen(2/3.x)
b) f(x) = 10sen(9.x)
c) f(x) = 10.sen(3.x)
d) f(x) = 5.sen(5/2.x)
Na função trigonométrica sen x ou cos x, os parâmetros A e w modificam suas características.
Determinação de A
A é a amplitude e altera a imagem da função, ou seja, os pontos máximos e mínimos que a função alcançará.
Nas funções senx e cos x, a imagem é [-1, 1]. O parâmetro A é um aplificador ou compressor da imagem, pois multiplacamos por ele, o resultado da função.
Sendo a imagem [-5, 5], A deve ser 5, pois: -1 . 5 = -5 e 1 . 5 = 5.
Determinação de
está multiplicando x, logo, modifica a função no eixo x. Ele comprime ou estica a função de forma inversamente proporcional. Isso siginifica que ele altera o período.
Se for maior que 1 ele comprime, se for menor que 1 estica.
Ao multiplicar por 1, o período é sempre 2, ao multiplicar por
, o período se tornou 3
. Escrevendo a proporção e resolvendo a regra de três:
A função é:
f(x) = 5.sen(2/3.x)
Questão 3
Dentre os gráficos abaixo, qual representa corretamente a função é
a) 
b) 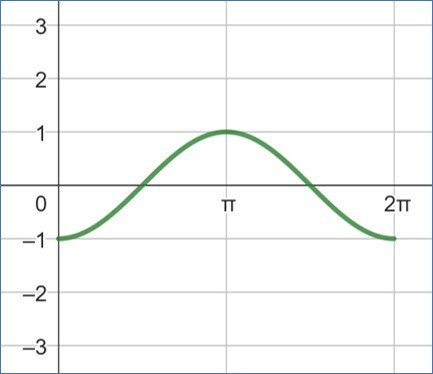
c) 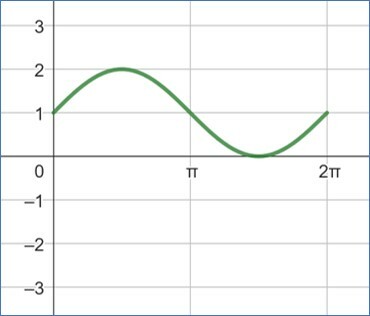
d) 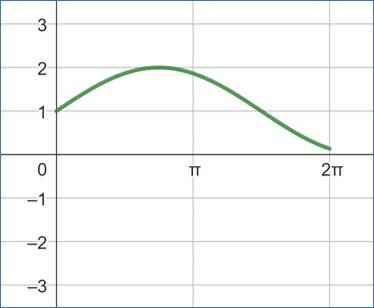
Questão 4
Um cometa com órbita elíptica passa próximo à Terra em intervalos regulares descritos pela função onde t representa o intervalo entre suas aparições em dezenas de anos. Suponha que a última aparição do cometa foi registrada em 1982. Este cometa passará pela Terra novamente em
2015
2035
2075.
2095
Precisamos determinar o período, tempo para um ciclo completo. Esta é o tempo em dezenas de anos para o cometa completar sua órbita e retornar para a Terra.
O período pode ser determinado pela relação:
Explicitando T:
O valor é o coeficiente de t, ou seja, o número que multiplica t, que na função dada pelo problema é
.
Considerando e substituindo os valores na fórmula, temos:
9,3 dezenas é igual a 93 anos.
Como a última aparição ocorreu em 1982, temos:
1982 + 93 = 2075
Conclusão
O cometa passará novamente em 2075.
Questão 5
(Enem 2021) Uma mola é solta da posição distendida conforme a figura. A figura à direita representa o gráfico da posição P (em cm) da massa m em função do tempo t (em segundo) em um sistema de coordenadas cartesianas. Esse movimento periódico é descrito por uma expressão do tipo P(t) = ± A cos (ωt) ou P(t) = ± A sen (ωt), em que A > 0 é a amplitude de deslocamento máximo e ω é a frequência, que se relaciona com o período T pela fórmula ω = 2π/T.
Considere a ausência de quaisquer forças dissipativas.
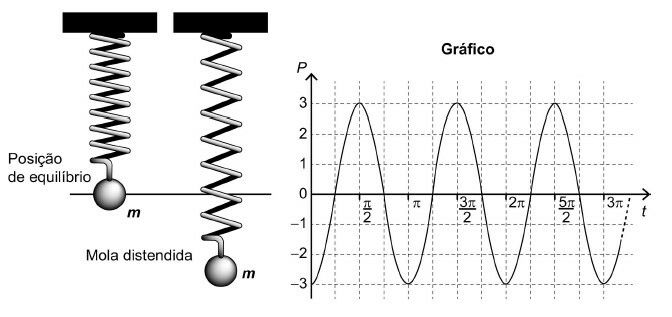
A expressão algébrica que representa as posições P(t) da massa m, ao longo do tempo, no gráfico, é
a) – 3 cos (2t)
b) – 3 sen (2t)
c) 3 cos (2t)
d) – 6 cos (2t)
e) 6 sen (2t)
Analisando o instante inicial t = 0, vemos que a posição é -3. Testaremos este par ordenado (0, -3) nas duas opções de função fornecidas no enunciado.
Para
Temos que seno de 0 é 0. Esta informação é obtida do círculo trigonométrico.
Assim, teríamos:
Esta informação é falsa, pois no tempo 0 a posição é -3. Ou seja, P(0) = -3. Assim, descartamos as opções com a função seno.
Testando para a função cosseno:
Mais uma vez, sabemos por meio do círculo trigonométrico que o cosseno de 0 é 1.
Do gráfico, vimos que a posição no tempo 0 é -3, por isso, A = -3.
Combinando estas informações, temos:
O período T é retirado do gráfico, ele é o comprimento entre dois picos ou dois vales, sendo T = .
A expressão para a frequência é fornecida pelo enunciado, sendo:
A resposta final é:
Questão 6
(Enem 2018) Em 2014 foi inaugurada a maior roda-gigante do mundo, a High Roller, situada em Las Vegas. A figura representa um esboço dessa roda-gigante, no qual o ponto A representa uma de suas cadeiras:
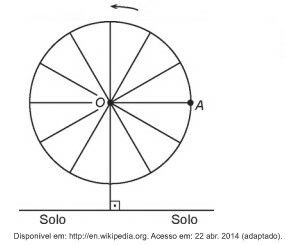
A partir da posição indicada, em que o segmento OA se encontra paralelo ao plano do solo, rotaciona-se a High Roller no sentido anti-horário, em torno do ponto O. Sejam t o ângulo determinado pelo segmento OA em relação à sua posição inicial, e f a função que descreve a altura do ponto A, em relação ao solo, em função de t.
Após duas voltas completas, f em o seguinte gráfico:
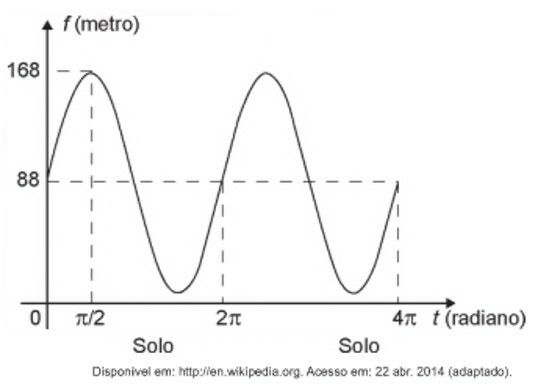
A expressão da função altura é dada por
a) f(t) = 80sen(t) + 88
b) f(t) = 80cos(t) + 88
c) f(t) = 88 cos(t)+168
d) f(t) = 168sen(t) + 88 cos(t)
e) f(t) = 88 sen(t)+ 168cos(t)
Para t = 0 a posição é 88.
cos(0) = 1
sen(0) = 0
Substituindo estes valores, na opção a, temos:
Questão 7
(CEDERJ 2014) O valor máximo da função real f(x) = 1 /(2+cos(x)) é:
a) 1/3
b) 1/2
c) 1
d) 3
O valor máximo ocorre quando o valor do denominador é o menor possível.
O termo 2 + cos(x) deve ser o menor possível. Assim, devemos pensar no menor valor possível que cos(x) pode assumir.
A função cos(x) varia entre -1 e 1. Substituindo o menor valor na equação:
Questão 8
(UECE 2021) No plano, com o sistema de coordenadas cartesianas usual, a interseção dos gráficos das funções reais de variável real f(x)=sen(x) e g(x)=cos(x) são, para cada número inteiro k, os pontos P(xk, yk). Então, os possíveis valores para yk são
a) √2/2 e – √2/2.
b) √2/3 e – √2/3.
c) √3/2 e – √3/2.
d) √3/3 e – √3/3.
Queremos determinar os valores de interseção das funções seno e cosseno que, como são periódicas, irão se repetir.
Os valores de seno e cosseno são iguais para os ângulos de 45° e 315°. Com a ajuda de uma tabela dos ângulos notáveis, para 45°, os valores de seno e cosseno de 45° são .
Para 315° estes valores são simétricos, ou seja, .
A opção correta é a letra a: e
.
Questão 9
Veja mais em:
- Funções Trigonométricas
- Exercícios de Trigonometria
- Exercícios de trigonometria no triângulo retângulo comentados
- Exercícios sobre círculo trigonométrico com resposta
- Índice de exercícios de matemática do 2º ano do Ensino Médio
ASTH, Rafael. Exercícios sobre funções trigonométricas (com respostas explicadas). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-funcoes-trigonometricas/. Acesso em:


