Exercícios sobre medidas de dispersão (com respostas explicadas)
As medidas de variabilidade fazem parte dos estudos da estatística, entre elas: amplitude, variância, desvio padrão e coeficiente de variação. Estas medidas fornecem uma medida da dispersão dos dados. Pratique com os exercícios resolvidos.
Questão 1
Uma loja de produtos para animais registrou o tempo (em minutos) que seus clientes passaram na loja em um determinado dia. Os tempos registrados foram os seguintes:
15, 20, 25, 30, 35, 40, 45, 50, 55, 60
A amplitude desse conjunto de dados é
a) 40
b) 45
c) 50
d) 55
e) 60
A amplitude é a diferença entre o maior e o menor valor do conjunto de dados.
Amplitude = Maior valor − Menor valor
Os dados já estão em Rol, ou seja, ordem crescente.
O menor valor é 15 e o maior valor é 60.
Amplitude = 60 − 15 = 45
Portanto, a resposta correta é b) 45.
Questão 2
Uma pesquisa foi realizada para registrar o número de horas de estudo semanal de estudantes. Os dados agrupados em intervalos são apresentados na tabela abaixo:

A amplitude das classes é de
a) 5 horas
b) 10 horas
c) 15 horas
d) 20 horas
e) 25 horas
A amplitude é a diferença entre o maior valor e o menor.
A = 5 - 0 = 5
Questão 3
Uma empresa está interessada na variabilidade do número de produtos vendidos diariamente. O número de produtos vendidos nos últimos 7 dias foi o seguinte:
15, 20, 18, 25, 22, 17, 21
A variância desse conjunto de dados é, mais aproximada de
a) 9
b) 11
c) 13
d) 15
e) 20
A variância é definida por:
Onde,
é a variância;
é i-ésimo dado no Rol;
é a média aritmética simples dos dados.
N é o número de dados.
Assim, N = 7 e a média é:
Subtraímos a média de cada ponto (elemento) do Rol, elevamos ao quadrado e somamos os resultados.
Para simplificar os cálculos, usamos apenas duas casas decimais.
Temos:
Estando mais próximo do valor 9, opção a.
Questão 4
Um estudo foi conduzido para avaliar o tempo diário gasto por alunos em atividades extracurriculares. Os dados agrupados em intervalos são apresentados na tabela abaixo:

A variância desse conjunto de dados é mais próxima de
a) 7.
b) 8.
c) 9.
d) 10.
e) 11.
Para calcular a variância com dados agrupados em classe, utilizamos a fórmula:
Onde,
é a variância;
é a i-ésima média de intervalo;
é a média dos dados.
N é o número de dados.
Cálculo de (média amostral).
Para calcular a média amostral, multiplicamos o ponto médio de cada intervalo por sua frequência, somamos os resultados e dividimos pela frequência acumulada.
O x é o ponto médio de cada classe, f a frequência e n a frequência total acumulada.
Fazer este cálculo utilizando uma tabela ajuda a organizar os dados.

Substituindo na fórmula da média:
Podemos calcular com ajuda de uma tabela:
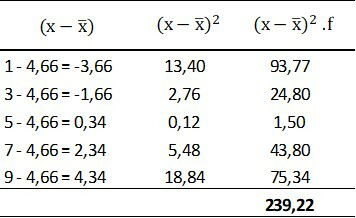
Para o cálculo da variância:
Questão 5
Uma pesquisa foi realizada para medir o tempo de espera (em minutos) dos clientes em um restaurante. Os dados agrupados em intervalos são apresentados na tabela abaixo:

O desvio padrão populacional do tempo de espera dos clientes é
a) 5,23
b) 6,47
c) 7,52
d) 8,32
e) 9,21
O Desvio Padrão é a raiz quadrada da Variância.
Muitos livros e autores utilizam símbolos próprios para designar o Desvio Padrão e a Variância, como a letra (sigma) para o Desvio Padrão populacional e S para o amostral.
Utilizemos VR² para variância populacional.
Onde:
x é o ponto médio para cada frequência;
é a média
N é total das frequências.
Neste problema, os dados estão agrupados em classes onde a segunda coluna mostra a distribuição das frequências para cada classe.
Precisamos calcular o ponto médio para cada classe, que chamaremos de x.
O ponto médio é dado por:
Para facilitar o cálculo, organizemos os dados em tabelas.
Cálculo da média
Devemos multiplicar cada ponto médio por sua frequência, somar os resultados e dividir pela soma das frequências.
Para o cálculo da variância, utilizaremos uma tabela para auxiliar nos cálculos do somatório.
Para o cálculo da variância:
Cálculo do desvio padrão
Questão 6
Um professor registrou as notas finais (em pontos) de sua turma em uma disciplina. As notas dos alunos foram as seguintes:
65, 70, 75, 80, 85, 90, 95, 100
Calcule o desvio padrão populacional dessas notas.
a) 11,45
b) 13,23
c) 15,56
d) 17,32
e) 19,47
O desvio padrão é a raiz quadrada da variância, sendo calculado por:
Sendo a variância:
Onde é a média.
Cálculo da variância:
Para o desvio padrão:
Questão 7
Um treinador está monitorando os tempos (em minutos) que um grupo de atletas leva para completar uma corrida de 5 km. Os tempos registrados são os seguintes:
18, 20, 22, 24, 26, 28, 30, 32, 34, 36
O coeficiente de variação desses tempos é
a) 14%
b) 17%
c) 21%
d) 27%
e) 38%
O coeficiente de variação (CV) é obtido pela divisão entre o desvio padrão e a média dos dados.
Cálculo da média:
Cálculo do desvio padrão:
Voltando ao problema inicial, podemos calcular o coeficiente de variação:
Em porcentagem
21%
Pratique mais exercícios de Desvio Padrão.
Veja mais sobre
- Medidas de Dispersão
- Variância e desvio padrão
- Desvio Padrão: o que é, fórmula, como calcular e exercícios
Referências Bibliográficas
Métodos Quantitativos Estatísticos./Guimarães, Paulo Ricardo Bittencourt. — Curitiba: IESDE Brasil S.A., 2008. p. 56.
ASTH, Rafael. Exercícios sobre medidas de dispersão (com respostas explicadas). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-medidas-de-dispersao/. Acesso em:


