Exercícios sobre triângulos (com respostas explicadas)
Pratique exercícios sobre triângulos com esta lista que preparamos. Os exercícios são explicados passo a passo para você tirar suas dúvidas e aprender tudo sobre este polígono de três lados.
Questão 1
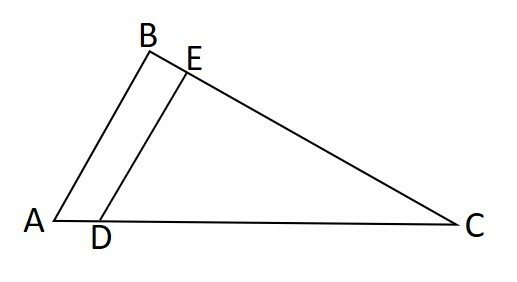
Analise a figura a seguir formada por triângulos, onde DE é paralelo a AB e, sabendo que:
CD = 15
AD = 1
AB = 8
Qual das opções representa o comprimento do lado DE?
a) 6,25
b) 7,00
c) 7,50
d) 8,53
Questão 2
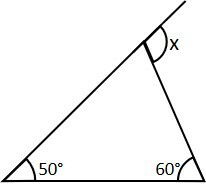
Na imagem abaixo, determine a opção em graus do valor do ângulo x.
a) 10º
b) 55º
c) 90º
d) 110º
Questão 3
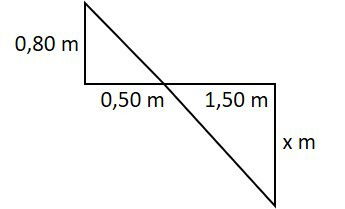
Determine o comprimento do segmento x.
a) 3,80 m
b) 2,40 m
c) 0,93 m
d) 1,3 m
Questão 4
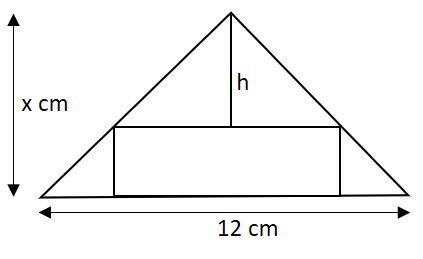
A figura abaixo mostra um retângulo de base de 8 cm e altura de 1 cm, inscrito em um triângulo. A base do retângulo coincide com a base do triângulo. Determine a medida da altura h.
a) 2,00 cm
b) 1,00 cm
c) 0,50 cm
d) 0,25 cm
Questão 5
Fernando é um carpinteiro e está separando ripas de madeira de diversos comprimentos para construir estruturas triangulares.
Dentre as seguintes opções de trios de ripas, a única capaz de formar um triângulo é
a) 3 cm, 7 cm, 11 cm
b) 6 cm, 4 cm, 12 cm
c) 3 cm, 4 cm, 5 cm
d) 7 cm, 9 cm, 18 cm
e) 2 cm, 6 cm, 9 cm
A condição de existência de um triângulo diz que cada um de seus lados deve ser menor que a soma dos outros dois.
A única opção que satisfaz esta condição é a letra c.
Questão 6
No triângulo abaixo, as retas e segmentos: verde, vermelha, azul e preta são: respectivamente:
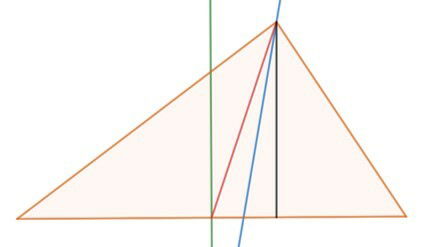
a) bissetriz, altura, mediatriz e mediana.
b) mediatriz, mediana, bissetriz e altura.
c) mediatriz, mediana, altura e bissetriz.
d) mediana, altura, bissetriz e mediatriz.
Questão 7
(ENCCEJA 2012) Uma colcha de retalhos, com formato retangular, é feita com quatro recortes triangulares de tecidos, conforme a figura.
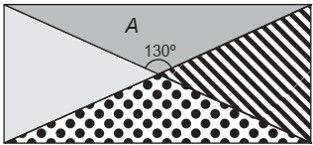
Considere que as costuras nos sentidos das diagonais dessa colcha são perfeitamente retilíneas.
O retalho A da colcha, que tem o formato de um triângulo, pode ser classificado quanto a seus ângulos internos e lados, respectivamente, como
a) acutângulo e equilátero.
b) obtusângulo e escaleno.
c) obtusângulo e isósceles.
d) retângulo e isósceles.
O retalho A é obtusângulo por possuir um ângulo obtuso, maior que 90º.
Sendo a colcha um retângulo e as separações dos triângulos formados por duas diagonais, os lados internos são iguais, dois a dois.
Como o retalho possui dois lados iguais, é isósceles.
Questão 8
No triângulo ABC exibido na figura a seguir, AD é a bissetriz do ângulo interno em A e . O ângulo interno em A é igual a
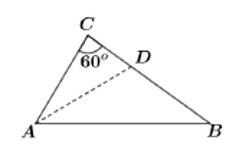
a) 60º
b) 70º
c) 80º
d) 90º
O segmento AD é uma bissetriz e divide o ângulo A em dois ângulos iguais.
Como o triângulo ADB possui dois lados iguais, AD e BD, ele é isósceles, e os ângulos da base são iguais.
Os triângulos isósceles possuem dois lados e dois ângulos iguais.
Assim, temos o ângulo de 60º e outros três iguais.
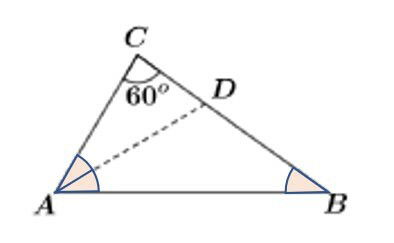
Sabemos que a soma dos ângulos internos de um triângulo é sempre igual a 180º.
Chamando de x o ângulo desconhecido, temos:
60 + x + x + x = 180
60 + 3x = 180
3x = 180 - 60
3x = 120
x = 120/3
x = 40
Se x = 40 e o ângulo em A é formado por 2x, logo:
A = 2x
A = 2 . 40 = 80º
Questão 9
(Enem 2011) Para determinar a distância de um barco até a praia, um navegante utilizou o seguinte procedimento: a partir de um ponto A, mediu o ângulo visual afazendo mira em um ponto fixo P da praia. Mantendo o barco no mesmo sentido, ele seguiu até um ponto B de modo que fosse possível ver o mesmo ponto P da praia, no entanto, sob um ângulo visual 2α. A figura ilustra essa situação:
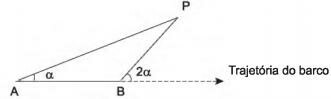
Suponha que o navegante tenha medido o ângulo α = 30º e, ao chegar ao ponto B, verificou que o barco havia percorrido a distância AB = 2 000 m. Com base nesses dados e mantendo a mesma trajetória, a menor distância do barco até o ponto fixo P será
a) 1 000 m.
b) 1 000√3 m.
c) 2 000√3/3 m.
d) 2 000 m.
e) 2 000√3 m
Resolução
Dados
= 30º
= 2 000 m
Passo 1: suplementar de 2.
Se o ângulo é de 30º, 2
= 60º e seu suplementar, o quanto falta para 180º, é de 120º, pois:
180 - 60 = 120
Passo 2: determinar os ângulos internos do triângulo ABP.
Como a soma dos ângulos internos de um triângulo é 180º, o ângulo deve ser 30º, pois:
30 + 120 + P = 180
P = 180 - 120 - 30
P = 30
Dessa forma, o triângulo ABP é isósceles e os lados AB e BP possuem a mesma medida de 2 000 m.
Passo 3: determinar a menor distância entre o barco e o ponto P.
A menor distância é o segmento perpendicular entre o ponto P e a linha pontilhada, que representa o trajeto do barco.
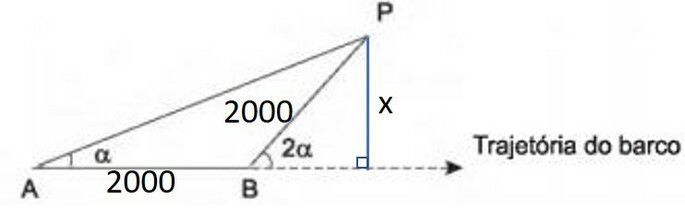
O segmento BP é a hipotenusa do triângulo retângulo.
O seno de 60º (2a) relaciona a distância x e a hipotenusa BP.
Conclusão
A menor distância entre o barco e o ponto P na praia é de 1000 m.
Questão 10
(UERJ - 2018)
Colho esta luz solar à minha volta,
No meu prisma a disperso e recomponho:
Rumor de sete cores, silêncio branco.
JOSÉ SARAMAGO
Na imagem a seguir, o triângulo ABC representa uma seção plana paralela à base de um prisma reto. As retas n e n’ são perpendiculares aos lados AC e AB , respectivamente, e BÂC = 80°.
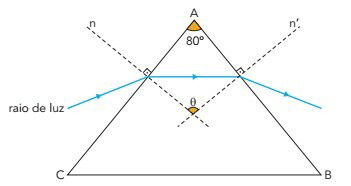
A medida do ângulo θ entre n e n’ é:
a) 90º
b) 100º
c) 110º
d) 120º
Passo 1: determinar os ângulos internos do triângulo com vértide de 80º.
No triângulo com vértice A de 80º e base formada pelo raio de luz, paralela à base maior, podemos determinar os ângulos internos.
Como o prisma é reto e a base de luz do triângulo com vértice em A é paralela à base maior, estes ângulos são iguais. Sendo a soma dos ângulos internos de um triângulo igual a 180º, temos:
80 + x + x = 180
2x = 180 - 80
2x = 100
x = 100/2
x = 50
Passo 2: determinar os ângulos internos do triângulo voltado para baixo, com vértice .
O ângulo x = 50 calculado anteriormente e o ângulo que cogitamos obter somam 90º
Assim, os ângulos internos do triângulo menor virado para baixo, são:
90–50 = 40
Usando mais uma vez a soma dos ângulos internos, temos:
40 + 40 + = 180
= 180 - 80
= 100º
Pratique mais exercícios com:
- Semelhança de Triângulos: exercícios comentados
- Exercícios sobre Teorema de Pitágoras
- Exercícios sobre ângulos (com questões respondidas)
Continue seus estudos sobre triângulos:
- Triângulo: tudo sobre este polígono
- Classificação dos triângulos
- Área do triângulo: como calcular?
- Trigonometria no triângulo retângulo
- Condição de existência de um triângulo (com exemplos)
ASTH, Rafael. Exercícios sobre triângulos (com respostas explicadas). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-triangulos-explicados/. Acesso em:

 :
:
