Fórmulas de Matemática

Rosimar Gouveia

Professora de Matemática e Física

As fórmulas matemáticas representam uma síntese do desenvolvimento de um raciocínio e são constituídas por números e letras.

Conhecê-las é necessário para resolver muitos problemas que são cobrados em concursos e no Enem, principalmente por reduzir, muitas vezes, o tempo de resolução de uma questão.

Contudo, apenas decorar as fórmulas não é suficiente para ter sucesso na sua aplicação. Saber o significado de cada grandeza e entender o contexto que cada fórmula deve ser empregada é fundamental.

Neste texto reunimos as principais fórmulas utilizadas no ensino médio, agrupadas por conteúdo.

Funções

As funções representam uma relação entre duas variáveis, de forma que um valor atribuído para uma delas corresponderá a um único valor da outra.

Duas variáveis podem estar associadas de diversas maneiras e de acordo com a sua regra de formação recebem diferentes classificações.

Função

Função Afim

f(x) = ax + b

a: coeficiente angular
b: coeficiente linear

Função Quadrática

f(x) = ax²+ bx + c , sendo a ≠ 0

a, b e c: coeficientes da função do 2º grau

Raízes da função quadrática

$bold italic x negrito igual a numerador negrito menos negrito b negrito mais ou menos raiz quadrada de negrito b à potência de negrito 2 negrito menos negrito 4 negrito. negrito a negrito. negrito c fim da raiz sobre denominador negrito 2 negrito a fim da fração$

Vértice da parábola

$bold italic x com negrito v subscrito negrito igual a numerador negrito menos negrito b sobre denominador negrito 2 negrito a fim da fração bold italic y com negrito v subscrito negrito igual a numerador negrito menos negrito incremento sobre denominador negrito 4 negrito a fim da fração$

Δ: discriminante da equação do 2º grau ( Δ = b² - 4.a.c)

a, b e c: coeficientes da equação do 2º grau

Função Modular

$bold italic f negrito parêntese esquerdo bold italic x negrito parêntese direito negrito igual a abre barra vertical negrito x fecha barra vertical negrito igual a abre chaves atributos de tabela alinhamento de coluna left fim dos atributos linha com célula com negrito x negrito vírgula negrito espaço negrito p negrito a negrito r negrito a negrito espaço negrito x negrito maior que ou igual a inclinado negrito 0 fim da célula linha com célula com negrito menos negrito x negrito vírgula negrito espaço negrito p negrito a negrito r negrito a negrito espaço negrito x negrito menor que negrito 0 fim da célula fim da tabela fecha$

Função Exponencial

f(x) = a^x, sendo a > 0 e a ≠ 0

Função Logarítmica

f(x) = log_ax , sendo a real positivo e a ≠ 1

Função Seno

f(x) = sen x

Função Cosseno

f(x) = cos x

Função Polinomial

f(x) = a_n. xⁿ + a_{n-1 .}x^n-1+ ... + a₂. x²+ a₁. x¹+ a₀

a_n, a_n-1, ... , a₂, a₁, a₀ : números complexos
n: número inteiro
x: variável complexa

Veja também:

Progressões

As progressões são sequências numéricas em que, a partir do primeiro termo, todos os demais são obtidos somando ou multiplicando por um mesmo valor.

Nas progressões chamadas de aritméticas, os termos posteriores são encontrados pela soma do termo anterior com um mesmo número (razão).

Já nas progressões geométricas, a sequência é formada pela multiplicação do termo anterior pela razão.

Progressão Aritmética

Termo Geral

a_n= a₁ + (n - 1) r

a_n: termo geral
a₁: 1º termo
n: número de termos
r: razão da PA

Soma de uma PA finita

$bold italic S com negrito n subscrito negrito igual a numerador negrito parêntese esquerdo negrito a com negrito 1 negrito espaço subscrito fim do subscrito negrito mais negrito a com negrito n subscrito negrito parêntese direito negrito n sobre denominador negrito 2 fim da fração$

S_n: soma dos n termos
a₁: 1º termo
a_n: enésimo termo
n: número de termos

Progressão Geométrica

Termo Geral

a_n = a₁. q^n-1

a_n: enésimo termo
a₁: 1º termo
q: razão da PG
n: número de termos

Soma de uma PG finita

$bold italic S com negrito n subscrito negrito igual a bold italic a com negrito 1 subscrito negrito. numerador negrito 1 negrito menos negrito q à potência de negrito n sobre denominador negrito 1 negrito menos negrito q fim da fração$

S_n: soma dos n termos
a₁: 1º termo
q: razão da PG
n: número de termos

Limite da soma de uma PG infinita

$pilha negrito l negrito i negrito m com negrito n negrito seta para a direita negrito infinito abaixo bold italic S com negrito n subscrito negrito igual a numerador negrito a com negrito 1 subscrito sobre denominador negrito 1 negrito menos negrito q fim da fração negrito vírgula negrito espaço negrito 0 negrito menor que abre barra vertical negrito q fecha barra vertical negrito menor que negrito 1$

$limite como n seta para a direita infinito de S com n subscrito$ : limite da soma quando o número de termos tende ao infinito
a₁: 1º termo
q: razão da PG
n: número de termos

Veja também:

Geometria Plana

A geometria plana é a parte da Matemática que estuda as propriedades das figuras geométricas no plano. O estudo da geometria envolve a aplicação de postulados, axiomas e teoremas.

Soma dos ângulos internos de um polígono

S_i = (n - 2) . 180º

S_i: soma dos ângulos internos
n: número de lados do polígono

Teorema de Tales

$numerador negrito A negrito B sobre denominador negrito C negrito D fim da fração negrito igual a numerador negrito A negrito ´ negrito B negrito ´ sobre denominador negrito C negrito ´ negrito D negrito ´ fim da fração$

AB e CD: segmentos de uma reta determinados pelo corte com um feixe de retas paralelas
A´B´ e C´D´: segmentos de uma outra reta, transversal a primeira, determinados pelo corte com o mesmo feixe de retas paralelas

Relações Métricas no triângulo retângulo

b² = a . n

a: hipotenusa
b: cateto
n: projeção do cateto b sobre a hipotenusa

c² = a . m

a: hipotenusa
c: cateto
m: projeção do cateto c sobre a hipotenusa

a.h = b . c

a: hipotenusa
b e c: catetos
h: altura relativa à hipotenusa

h² = m . n

h: altura relativa à hipotenusa
m: projeção do cateto c sobre a hipotenusa
n: projeção do cateto b sobre a hipotenusa

a² = b² + c² (Teorema de Pitágoras)

a: hipotenusa
b e c: catetos

Polígono inscrito na circunferência

Triângulo equilátero inscrito

$Error converting from MathML to accessible text.$

$caligráfica l com 3 subscrito$ : medida do lado do triângulo inscrito
r: raio da circunferência

$bold italic a com negrito 3 subscrito negrito igual a negrito r sobre negrito 2$

r: raio da circunferência
a₃: apótema do triângulo equilátero inscrito

Quadrado inscrito

$Error converting from MathML to accessible text.$

$caligráfica l com 4 subscrito$ : medida do lado do quadrado inscrito
r: raio da circunferência

$bold italic a com negrito 4 subscrito negrito igual a numerador negrito r raiz quadrada de negrito 2 sobre denominador negrito 2 fim da fração$
a₄: apótema do quadrado inscrito
r: raio da circunferência

Hexágono regular inscrito

$Error converting from MathML to accessible text.$

$caligráfica l com 6 subscrito dois pontos$ medida do lado do hexágono inscrito
r: raio da circunferência

$bold italic a com negrito 6 subscrito negrito igual a numerador negrito r raiz quadrada de negrito 3 sobre denominador negrito 2 fim da fração$
a₆: apótema do hexágono inscrito
r: raio da circunferência

Comprimento da circunferência

C = 2.π.r

C: comprimento da circunferência
r: raio da circunferência

Área de figuras planas

Área do triângulo

$bold italic A negrito igual a numerador negrito b negrito. negrito h sobre denominador negrito 2 fim da fração$

A: área do triângulo
b: medida da base
h: medida da altura relativa à base

Fórmula de Heron para área do triângulo

$bold italic A negrito igual a raiz quadrada de negrito p negrito parêntese esquerdo negrito p negrito menos negrito a negrito parêntese direito negrito parêntese esquerdo negrito p negrito menos negrito b negrito parêntese direito negrito parêntese esquerdo negrito p negrito menos negrito c negrito parêntese direito fim da raiz$

p: semiperímetro $abre parênteses bold italic p negrito igual a numerador negrito a negrito mais negrito b negrito mais negrito c sobre denominador negrito 2 fim da fração fecha parênteses$
a, b e c: lados do triângulo

Área do triângulo equilátero

$Error converting from MathML to accessible text.$

A: área do triângulo equilátero
$caligráfica l dois pontos$ medida do lado do triângulo equilátero

Área do retângulo

A = b.h

A: área do retângulo
b: medida da base
h: medida da altura

Área do quadrado

A = L²

A: área do quadrado
L: medida do lado

Área do paralelogramo

A = b.h

A: área do paralelogramo
b: base
h: altura

Área do trapézio

$bold italic A negrito igual a numerador abre parênteses negrito B negrito mais negrito b fecha parênteses negrito h sobre denominador negrito 2 fim da fração$

A: área do trapézio
B: medida da base maior
b: medida da base menor
h: medida da altura

Área do losango

$bold italic A negrito igual a numerador negrito D negrito. negrito d sobre denominador negrito 2 fim da fração$

A: área do losango
D: medida da diagonal maior
d: medida da diagonal menor

Área do hexágono regular

$Error converting from MathML to accessible text.$

A: área do hexágono regular
$caligráfica l dois pontos$ medida do lado do hexágono

Área do círculo

A = π. r²

A: área do círculo
r: medida do raio

Área do setor circular

$bold italic A negrito igual a numerador negrito alfa com negrito r negrito a negrito d subscrito fim do subscrito negrito. bold italic r à potência de negrito 2 sobre denominador negrito 2 fim da fração negrito igual a numerador negrito alfa com negrito g negrito r negrito a negrito u negrito s subscrito fim do subscrito negrito. negrito pi negrito. bold italic r à potência de negrito 2 sobre denominador negrito 360 negrito º fim da fração$

A: área do setor circular
α_rad: ângulo em radianos
R: raio
α_graus: ângulo em graus

Veja mais:

Trigonometria

A trigonometria é a parte da matemática que estuda as relações existentes entre os lados e os ângulos dos triângulos.

Ela é utilizada também em outras áreas de estudo como por exemplo na física, geografia, astronomia, engenharia, entre outras.

Relações Trigonométricas

$bold italic s bold italic e bold italic n negrito espaço negrito B com negrito conjunção lógica sobrescrito negrito igual a negrito b sobre negrito a$

sen $B com conjunção lógica sobrescrito$ : seno do ângulo B
b: cateto oposto ao ângulo B
a: hipotenusa

$bold italic c bold italic o bold italic s negrito espaço negrito B com negrito conjunção lógica sobrescrito negrito igual a negrito c sobre negrito a$

cos $B com conjunção lógica sobrescrito$ : cosseno do ângulo B
c: cateto adjacente ao ângulo B
a: hipotenusa

$bold italic t bold italic g negrito espaço negrito B com negrito conjunção lógica sobrescrito negrito igual a negrito b sobre negrito c$

tg $B com conjunção lógica sobrescrito$ : tangente do ângulo B
b: cateto oposto ao ângulo B
c: cateto adjacente ao ângulo B

sen² α + cos² α = 1

sen α: seno do ângulo α
cos α: cosseno do ângulo α

$bold italic t bold italic g negrito espaço bold italic alfa negrito igual a numerador negrito s negrito e negrito n negrito espaço negrito alfa sobre denominador negrito c negrito o negrito s negrito espaço negrito alfa fim da fração$

tg α: tangente do ângulo α
sen α: seno do ângulo α
cos α: cosseno do ângulo α

$bold italic c bold italic o bold italic t bold italic g negrito espaço bold italic alfa negrito igual a numerador negrito 1 sobre denominador negrito t negrito g negrito espaço negrito alfa fim da fração negrito igual a numerador negrito c negrito o negrito s negrito espaço negrito alfa sobre denominador negrito s negrito e negrito n negrito espaço negrito alfa fim da fração$

cotg α: cotangente do ângulo α
tg α: tangente do ângulo α
sen α: seno do ângulo α
cos α: cosseno do ângulo α
$bold italic s bold italic e bold italic c negrito espaço bold italic alfa negrito igual a numerador negrito 1 sobre denominador negrito c negrito o negrito s negrito espaço negrito alfa fim da fração$

sec α: secante do ângulo α
cos α: cosseno do ângulo α

$bold italic c bold italic o bold italic s bold italic s bold italic e bold italic c negrito espaço bold italic alfa negrito igual a numerador negrito 1 sobre denominador negrito s negrito e negrito n negrito espaço negrito alfa fim da fração$

cossec α: cossecante do ângulo α
sen α: seno do ângulo α

tg² α + 1 = sec² α

tg α: tangente do ângulo α
sec α: secante do ângulo α

cotg² α + 1 = cossec² α

cotg α: cotangente do ângulo α
cossec α: cossecante do ângulo α

Lei dos senos

$numerador negrito a sobre denominador negrito s negrito e negrito n negrito espaço negrito A com negrito conjunção lógica sobrescrito fim da fração negrito igual a numerador negrito b sobre denominador negrito s negrito e negrito n negrito espaço negrito B com negrito conjunção lógica sobrescrito fim da fração negrito igual a numerador negrito c sobre denominador negrito s negrito e negrito n negrito espaço negrito C com negrito conjunção lógica sobrescrito fim da fração$

a: medida do lado
sen $A com conjunção lógica sobrescrito$ : seno do ângulo oposto ao lado a
b: medida do lado
sen $B com conjunção lógica sobrescrito$ : seno do ângulo oposto ao lado b
c: medida do lado
sen $C com conjunção lógica sobrescrito$ : seno do ângulo oposto ao lado c

Lei dos cossenos

a² = b² + c² - 2.b.c.cos $A com conjunção lógica sobrescrito$

a, b e c: lados do triângulo
cos $A com conjunção lógica sobrescrito$ : cosseno do ângulo oposto ao lado a

Transformações trigonométricas

Seno da soma de dois arcos

sen (a + b) = sen a . cos b + sen b.cos a

sen (a + b): seno da adição do arco a com o arco b
sen a: seno do arco a
cos b: cosseno do arco b
sen b: seno do arco b
cos a: cosseno do arco a

Seno da diferença de dois arcos

sen (a - b) = sen a . cos b - sen b.cos a

sen (a - b): seno da subtração do arco a com o arco b
sen a: seno do arco a
cos b: cosseno do arco b
sen b: seno do arco b
cos a: cosseno do arco a

Cosseno da soma de dois arcos

cos (a + b) = cos a . cos b - sen a.sen b

cos (a + b): cosseno da adição do arco a com o arco b
cos a: cosseno do arco a
cos b: cosseno do arco b
sen a: seno do arco a
sen b: seno do arco b

Cosseno da diferença de dois arcos

cos (a - b) = cos a . cos b + sen a.sen b

cos (a - b): cosseno da subtração do arco a com o arco b
cos a: cosseno do arco a
cos b: cosseno do arco b
sen a: seno do arco a
sen b: seno do arco b

Tangente da soma de dois arcos

$bold italic t bold italic g negrito espaço negrito parêntese esquerdo bold italic a negrito mais bold italic b negrito parêntese direito negrito espaço negrito igual a negrito espaço numerador negrito t negrito g negrito espaço negrito a negrito espaço negrito mais negrito espaço negrito t negrito g negrito espaço negrito b sobre denominador negrito 1 negrito espaço negrito menos negrito espaço negrito t negrito g negrito espaço negrito a negrito espaço negrito. negrito espaço negrito t negrito g negrito espaço negrito b fim da fração$

tg (a + b): tangente da adição do arco a com o arco b (arcos em que a tangente é definida)
tg a: tangente do arco a
tg b: tangente do arco b

Tangente da diferença de dois arcos

$bold italic t bold italic g negrito espaço negrito parêntese esquerdo bold italic a negrito menos bold italic b negrito parêntese direito negrito espaço negrito igual a negrito espaço numerador negrito tg negrito espaço negrito a negrito espaço negrito menos negrito espaço negrito tg negrito espaço negrito b sobre denominador negrito 1 negrito espaço negrito mais negrito espaço negrito tg negrito espaço negrito a negrito espaço negrito. negrito espaço negrito tg negrito espaço negrito b fim da fração$

tg (a - b): tangente da subtração do arco a com o arco b (arcos em que a tangente é definida)
tg a: tangente do arco a
tg b: tangente do arco b

Veja mais:

Análise Combinatória

Na análise combinatória estudamos os métodos e técnicas que permitem resolver problemas relacionados com contagem.

As fórmulas utilizadas neste conteúdo são, muitas vezes, empregadas na resolução de problemas de probabilidade.

Permutação simples

P = n!

n!: n . (n - 1) . (n - 2). ... . 3 . 2 . 1

Arranjo simples

$bold italic A com negrito n negrito vírgula negrito p subscrito fim do subscrito negrito igual a numerador negrito n negrito fatorial sobre denominador negrito parêntese esquerdo negrito n negrito menos negrito p negrito parêntese direito negrito fatorial fim da fração$

Combinação simples

$bold italic C com negrito n negrito vírgula negrito p subscrito fim do subscrito negrito igual a numerador negrito n negrito fatorial sobre denominador negrito p negrito fatorial negrito espaço negrito parêntese esquerdo negrito n negrito menos negrito p negrito parêntese direito negrito fatorial fim da fração$

Binômio de Newton

$bold italic T com negrito k negrito mais negrito 1 subscrito fim do subscrito negrito igual a abre parênteses tabela linha com negrito n linha com negrito k fim da tabela fecha parênteses bold italic x à potência de negrito n negrito menos negrito k fim do exponencial bold italic y à potência de negrito k$

T_k+1: termo geral
$abre parênteses tabela linha com n linha com k fim da tabela fecha parênteses dois pontos espaço n ú m e r o espaço b i n o m i a l espaço n espaço s o b r e espaço k espaço abre parênteses numerador negrito n negrito fatorial sobre denominador negrito p negrito fatorial negrito parêntese esquerdo negrito n negrito menos negrito p negrito parêntese direito negrito fatorial fim da fração fecha parênteses$

Veja também

Exercícios de Análise Combinatória.

Permutação

Probabilidade

O estudo da probabilidade permite obter o valor das ocorrências possíveis num experimento aleatório (fenômeno aleatório). Em outras palavras, a probabilidade analisa as “chances” de obter determinado resultado.

$bold italic p negrito espaço negrito parêntese esquerdo bold italic A negrito parêntese direito negrito espaço negrito igual a numerador negrito n negrito parêntese esquerdo negrito A negrito parêntese direito sobre denominador negrito n negrito parêntese esquerdo negrito ómega maiúsculo negrito parêntese direito fim da fração$

p (A): probabilidade de ocorrência de um evento A
n(A): número de resultados favoráveis
n(Ω): número de resultados possíveis

Probabilidade da união de dois eventos

p(A U B) = p(A) + p(B) - p(A ∩ B)

p(A U B): probabilidade de ocorrer o evento A ou o evento B
p(A): probabilidade de ocorrer o evento A
p(B): probabilidade de ocorrer o evento B
p(A ∩ B): probabilidade de ocorrer o evento A e o evento B

Probabilidade de eventos mutuamente exclusivos

p(A U B) = p(A) + p(B)

p(A U B): probabilidade de ocorrer o evento A ou o evento B
p(A): probabilidade de ocorrer o evento A
p(B): probabilidade de ocorrer o evento B

Probabilidade condicional

$bold italic p negrito parêntese esquerdo bold italic A negrito dividido por bold italic B negrito parêntese direito negrito igual a numerador negrito p negrito parêntese esquerdo negrito A negrito intersecção negrito B negrito parêntese direito sobre denominador negrito p negrito parêntese esquerdo negrito B negrito parêntese direito fim da fração$

p(A/B): probabilidade de ocorrer o evento A tendo ocorrido o evento B
p(A ∩ B): probabilidade de ocorrer o evento A e o evento B
p(B): probabilidade de ocorrer o evento B

Probabilidade de eventos independentes

p(A ∩ B) = p(A).p(B)

p(A ∩ B): probabilidade de ocorrer o evento A e o evento B
p(A): probabilidade de ocorrer o evento A
p(B): probabilidade de ocorrer o evento B

Veja também Exercícios de Probabilidade.

Estatística

Em estatística estudamos a coleta, registro, organização e análise dos dados de uma pesquisa.

Utilizando fórmulas matemáticas é possível conhecer as informações relativas a uma determinada população a partir dos dados de uma amostra desta população.

Média aritmética

$Error converting from MathML to accessible text.$

M_A: média aritmética
$soma de i igual a 1 para n de x com i subscrito$ : soma de todos os valores da amostra
n: quantidade de dados da amostra

Variância

$Error converting from MathML to accessible text.$

V: variância
(x_i - M_A): desvio dos valores x em relação a média aritmética
n: quantidade de dados da amostra

Desvio padrão

$bold italic D bold italic P negrito espaço negrito igual a raiz quadrada de negrito V$

DP: desvio padrão
V: variância

Veja também Estatística e Estatística - Exercícios

Matemática Financeira

Estudar a equivalência de capitais no tempo é o foco da matemática financeira, utilizando fórmulas que nos permitem conhecer como varia o valor do dinheiro no decorrer do tempo.

Juros simples

J = C . i . t

J: juros
C: capital
i: taxa de juros
t: tempo de aplicação

M = C + J

M: montante
C: capital
J: juros

Juros compostos

M = C ( 1 + i)^t

M. montante
C: capital
i: taxa de juros
t: tempo de aplicação

J = M - C

J: juros
M: montante
C: capital

Veja mais:

Geometria Espacial

A Geometria Espacial corresponde a área da matemática que se encarrega de estudar as figuras no espaço, ou seja, aquelas que possuem mais de duas dimensões.

Relação de Euler

V - A + F = 2

V: número de vértices
A: número de arestas
F: número de faces

Prisma

$bold italic d negrito igual a raiz quadrada de negrito a à potência de negrito 2 negrito mais negrito b à potência de negrito 2 negrito mais negrito c à potência de negrito 2 fim da raiz$

d: diagonal do paralelepípedo
a, b e c: medidas das dimensões do paralelepípedo

V = B . h

V: volume do prisma
B: área da base
h: altura do prisma

Pirâmide

$bold italic V negrito igual a negrito 1 sobre negrito 3 bold italic B negrito. bold italic h$

V: volume da pirâmide
B: área da base
h: altura da pirâmide

Tronco de pirâmide

$bold italic V negrito igual a negrito h sobre negrito 3 negrito parêntese esquerdo bold italic B negrito mais raiz quadrada de negrito B negrito b fim da raiz negrito mais bold italic b negrito parêntese direito$

V: volume do tronco de pirâmide
h: altura do tronco de pirâmide
B: área da base maior
b: área da base menor

Cilindro

A_L= 2.π.R.h

A_L: área lateral
R: raio
h: altura do cilindro

A_B = 2.π.R²

A_B: área da base
R: raio

A_T = 2.π.R (h + R)

A_T: área total
R: raio
h: altura

V = π.R².h

V: volume
R: raio

Cone

A_L= π.R. g

A_L: área lateral
R: raio
g: geratriz

A_B = π.R²

A_B: área da base
R: raio

A_T = π.R.(g + R)

A_T : área total
R: raio
g: geratriz

$bold italic V negrito igual a negrito 1 sobre negrito 3 bold italic A com negrito B subscrito negrito. bold italic h$

V: volume
A_B: área da base
h: altura

Tronco de cone

A_L = π.g (R + r)

A_L: área lateral
g: geratriz
R: raio maior
r: raio menor

$bold italic V negrito igual a numerador negrito pi negrito h sobre denominador negrito 3 fim da fração negrito parêntese esquerdo bold italic R à potência de negrito 2 negrito mais bold italic R bold italic r negrito mais bold italic r à potência de negrito 2 negrito parêntese direito$

V: volume
h: altura
R: raio maior
r: raio menor

Esfera

A = 4. π.R²

A: área da esfera
R: raio

$bold italic V negrito igual a negrito 4 sobre negrito 3 bold italic pi bold italic R à potência de negrito 3$

V: volume da esfera
R: raio

Veja mais:

Geometria Analítica

Em geometria analítica representamos retas, circunferências, elipses, entre outras no plano cartesiano. Assim, é possível descrever essas formas geométricas por meio de equações.

$bold italic d negrito espaço negrito parêntese esquerdo bold italic A negrito vírgula bold italic B negrito parêntese direito negrito espaço negrito igual a negrito espaço raiz quadrada de negrito parêntese esquerdo negrito x com negrito 2 subscrito negrito menos negrito x com negrito 1 subscrito negrito parêntese direito à potência de negrito 2 negrito espaço negrito mais negrito espaço negrito parêntese esquerdo negrito y com negrito 2 subscrito negrito menos negrito y com negrito 1 subscrito negrito parêntese direito à potência de negrito 2 fim da raiz$

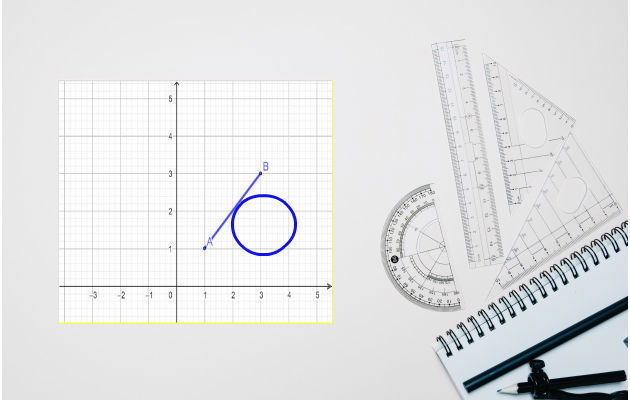
d (A,B): distância entre os pontos A e B
x₁: abscissa do ponto A
x₂: abscissa do ponto B
y₁: abscissa do ponto A
y₂: abscissa do ponto B

$bold italic m negrito igual a numerador negrito y com negrito 2 subscrito negrito menos negrito y com negrito 1 subscrito sobre denominador negrito x com negrito 2 subscrito negrito menos negrito x com negrito 1 subscrito fim da fração$

m: coeficiente angular da reta
x₁: abscissa do ponto A
x₂: abscissa do ponto B
y₁: abscissa do ponto A
y₂: abscissa do ponto B

Equação geral da reta

ax + by + c = 0

a, b e c: constantes

Equação reduzida da reta

y = mx + b

m: coeficiente angular
b: coeficiente linear

Equação segmentária da reta

$negrito x sobre negrito a negrito mais negrito y sobre negrito b negrito igual a negrito 1$

a: valor em que a reta intersecta o eixo x
b: valor em que a reta intersecta o eixo y

Distância entre um ponto e uma reta

$bold italic d negrito igual a numerador abre barra vertical negrito a negrito x negrito mais negrito b negrito y negrito mais negrito c fecha barra vertical sobre denominador raiz quadrada de negrito a à potência de negrito 2 negrito mais negrito b à potência de negrito 2 fim da raiz fim da fração$

d: distância entre o ponto e a reta
a, b e c: coeficientes da reta
x: abscissa do ponto
y: ordenada do ponto

Ângulo entre duas retas

$bold italic t bold italic g negrito espaço bold italic alfa negrito igual a abre barra vertical numerador negrito m com negrito 1 subscrito negrito menos negrito m com negrito 2 subscrito sobre denominador negrito 1 negrito mais negrito m com negrito 1 subscrito negrito m com negrito 2 subscrito fim da fração fecha barra vertical$

m₁: coeficiente angular da reta 1
m₂: coeficiente angular da reta 2

Circunferência

Equação da circunferência

(x - x_c)² + (y - y_c)² = R²

x e y: coordenadas de um ponto qualquer pertencente a circunferência
x_ce y_c: coordenadas do centro da circunferência
R: raio

Equação normal da circunferência

x² + y² - 2.x_c.x - 2.y_c.y + (x_c²+ y_c² - R²) = 0

x e y: coordenadas de um ponto qualquer pertencente a circunferência
x_ce y_c: coordenadas do centro da circunferência
R: raio

Elipse

$negrito x à potência de negrito 2 sobre negrito a à potência de negrito 2 negrito mais negrito y à potência de negrito 2 sobre negrito b à potência de negrito 2 negrito igual a negrito 1$ (o eixo maior pertence ao eixo x)

x e y: coordenadas de um ponto qualquer pertencente a elipse
a: medida do semi-eixo maior
b: medida do semi-eixo menor

$negrito y à potência de negrito 2 sobre negrito a à potência de negrito 2 negrito mais negrito x à potência de negrito 2 sobre negrito b à potência de negrito 2 negrito igual a negrito 1$ (o eixo maior pertence ao eixo y)

x e y: coordenadas de um ponto qualquer pertencente a elipse
a: medida do semi-eixo maior
b: medida do semi-eixo menor

Hipérbole

$negrito x à potência de negrito 2 sobre negrito a à potência de negrito 2 negrito menos negrito y à potência de negrito 2 sobre negrito b à potência de negrito 2 negrito igual a negrito 1$ (o eixo real pertence ao eixo x)

x e y: coordenadas de um ponto qualquer pertencente a hipérbole
a: medida do semi-eixo real
b: medida do semi-eixo imaginário

$negrito y à potência de negrito 2 sobre negrito a à potência de negrito 2 negrito menos negrito x à potência de negrito 2 sobre negrito b à potência de negrito 2 negrito igual a negrito 1$ (o eixo real pertence ao eixo y)

x e y: coordenadas de um ponto qualquer pertencente a hipérbole
a: medida do semi-eixo real
b: medida do semi-eixo imaginário

Parábola

y² = 2.p.x (vértice na origem e foco no eixo das abscissa)

x e y: coordenadas de um ponto qualquer pertencente a parábola
p: parâmetro

x² = 2.p.y (vértice na origem e foco no eixo das ordenadas)

x e y: coordenadas de um ponto qualquer pertencente a parábola
p: parâmetro

Números Complexos

Os números complexos são números compostos por uma parte real e uma imaginária. A parte imaginária é representada pela letra i e indica o resultado da equação i² = -1.

Forma algébrica

z = a + b.i

z: número complexo
a: parte real
bi: parte imaginária (sendo i = √−1)

Forma trigonométrica

$bold italic z negrito igual a bold italic ró negrito parêntese esquerdo bold italic c bold italic o bold italic s bold italic teta negrito mais bold italic i negrito espaço bold italic s bold italic e bold italic n bold italic teta negrito parêntese direito$

z: número complexo
ρ: módulo do número complexo ( $ró igual a raiz quadrada de a ao quadrado mais b ao quadrado fim da raiz$ )
Θ: argumento de z

$bold italic z à potência de negrito n negrito igual a bold italic ró à potência de negrito n abre colchetes negrito c negrito o negrito s negrito parêntese esquerdo negrito n negrito teta negrito parêntese direito negrito mais negrito i negrito espaço negrito s negrito e negrito n negrito parêntese esquerdo negrito n negrito teta negrito parêntese direito fecha colchetes$ ( fórmula de Moivre)

z: número complexo
ρ: módulo do número complexo
n: expoente
Θ: argumento de z

Veja também: Exercícios sobre Números Complexos

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.