Grandezas proporcionais

Rafael C. Asth

Professor de Matemática e Física

As grandezas proporcionais têm seus valores aumentados ou diminuídos em uma relação que pode ser classificada como proporcionalidade direta ou inversa.

Uma grandeza é definida como algo que pode ser medido ou calculado, seja velocidade, área ou volume de um material, e é útil para comparar com outras medidas, muitas vezes de mesma unidade, representando uma razão.

A proporção é uma relação de igualdade entre razões e, assim, apresenta a comparação de duas grandezas em diferentes situações.

$reto a sobre reto b igual a reto c sobre reto d$

A igualdade entre a, b, c e d é lida da seguinte forma: a está para b, assim como c está para d.

A relação entre as grandezas podem ocorrer de maneira diretamente, inversamente proporcional ou mesmo sem nenhuma relação.

Quando a variação de uma grandeza faz com que a outra varie na mesma proporção, temos uma proporcionalidade direta. A proporcionalidade inversa é observada quando a mudança em uma grandeza produz uma alteração oposta na outra.

Proporcionalidade direta

Duas grandezas são diretamente proporcionais quando a variação de uma implica na variação da outra na mesma proporção, ou seja, duplicando uma delas, a outra também duplica; reduzindo pela metade, a outra também reduz na mesma quantidade... e assim por diante.

Graficamente a variação diretamente proporcional de uma grandeza em relação à outra forma uma reta que passa pela origem, pois temos y = k.x, sendo k uma constante.

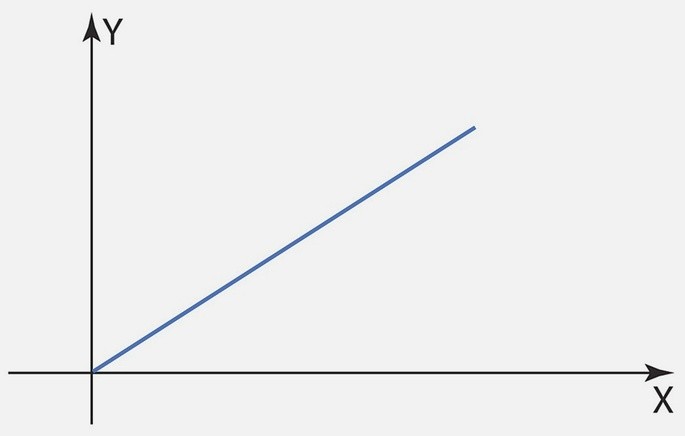
gráfico de grandezas diretamente proporcionais — Gráfico de y proporcional a x

Exemplo de proporcionalidade direta

Uma impressora, por exemplo, tem a capacidade de imprimir 10 páginas por minuto. Se dobrarmos o tempo, dobramos a quantidade de páginas impressas. Da mesma forma, se pararmos a impressora na metade de um minuto, teremos a metade do número de impressões esperadas.

Agora, veremos com números a relação entre as duas grandezas.

Em uma gráfica são feitas impressões de livros escolares. Em 2 horas, são realizadas 40 impressões. Em 3 horas, a mesma máquina produz mais 60 impressões, em 4 horas, 80 impressões, e, em 5 horas, 100 impressões.

Tempo (horas)	2	3	4	5
Impressões (número)	40	60	80	100

A constante de proporcionalidade entre as grandezas é encontrada pela razão entre o tempo de trabalho da máquina e o número de cópias realizadas.

$tabela linha com célula com 2 sobre 40 fim da célula igual a célula com 3 sobre 60 fim da célula igual a célula com 4 sobre 80 fim da célula igual a fim da tabela tabela linha com célula com 5 sobre 100 fim da célula igual a célula com 1 sobre 20 fim da célula fim da tabela$

O quociente dessa sequência (1/20) recebe o nome de constante de proporcionalidade (k).

O tempo de trabalho (2, 3, 4 e 5) é diretamente proporcional ao número de cópias (40, 60, 80 e 100), pois ao dobrar o tempo de trabalho o número de cópias também dobra.

Cálculo de grandeza diretamente proporcional com regra de três

Para calcular um valor desconhecido entre grandezas diretamente proporcionais, podemos usar a Regra de Três.

No exemplo anterior da gráfica, em 5 horas, quantos livros serão impressos?

2 horas imprimem 40 livros
5 horas imprimem x livros

↑ mais horas de trabalho = ↑ mais livros impressos (grandezas diretas)

$2 sobre 40 igual a 5 sobre x$

Usando a propriedade fundamental das proporções, temos:

$2. x igual a 5.40 2 x igual a 200 x igual a 200 sobre 2 x igual a 100$

Como havíamos visto na tabela, em 5 h, 100 livros são impressos.

Proporcionalidade inversa

Duas grandezas são inversamente proporcionais quando o aumento de uma implica na redução da outra, ou seja, dobrando uma grandeza, a correspondente reduz pela metade; triplicando uma grandeza, a outra reduz para terça parte... e assim por diante.

Graficamente a variação inversamente proporcional de uma grandeza em relação à outra forma uma hipérbole, pois temos y = k/x, sendo k uma constante.

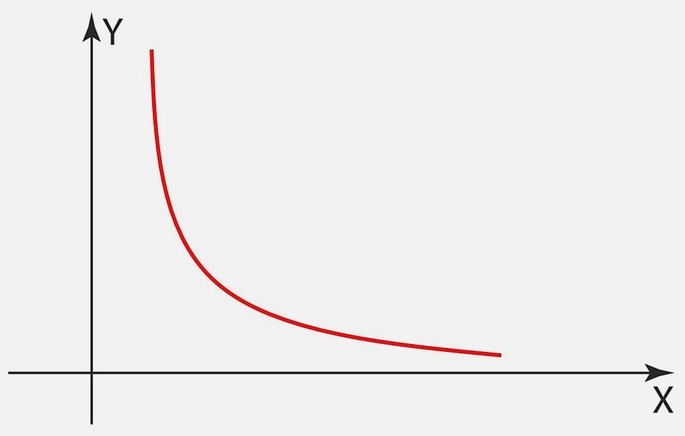
gráfico de grandezas inversamente proporcionais — Gráfico de y inversamente proporcional a x

Exemplo de proporção inversa

Quando se aumenta a velocidade, o tempo para concluir um percurso é menor. Da mesma forma, ao diminuir a velocidade mais tempo será necessário para fazer o mesmo trajeto.

Confira a seguir uma aplicação de relação entre essas grandezas.

João decidiu contar o tempo que levava indo de casa à escola de bicicleta com diferentes velocidades. Observe a sequência registrada.

Tempo (min)	2	4	5	1
Velocidade (m/s)	30	15	12	60

Podemos fazer a seguinte relação com os números das sequências:

$tabela linha com célula com 2 espaço. espaço 30 fim da célula igual a célula com 4 espaço. espaço 15 fim da célula igual a célula com 5 espaço. espaço 12 fim da célula igual a fim da tabela tabela linha com célula com 1 espaço. espaço 60 fim da célula igual a 60 fim da tabela$

Escrevendo como igualdade de razões, temos:

$tabela linha com célula com numerador 2 sobre denominador começar estilo mostrar 1 sobre 30 fim do estilo fim da fração fim da célula igual a célula com numerador 4 sobre denominador começar estilo mostrar 1 sobre 15 fim do estilo fim da fração fim da célula igual a célula com numerador 5 sobre denominador começar estilo mostrar 1 sobre 12 fim do estilo fim da fração fim da célula igual a fim da tabela tabela linha com célula com numerador 1 sobre denominador começar estilo mostrar 1 sobre 60 fim do estilo fim da fração fim da célula fim da tabela$

Nesse exemplo, a sequência de tempo (2, 4, 5 e 1) é inversamente proporcional à velocidade média pedalando (30, 15, 12 e 60) e a constante de proporcionalidade (k) entre essas grandezas é 60.

Observe que quando um número de uma sequência dobra, o número da sequência correspondente reduz pela metade.

Cálculo de grandeza inversamente proporcional com regra de três

No exemplo do João indo de casa à escola de bicicleta.

↑ maior velocidade = ↓ menor tempo (grandezas inversas)

Andando a 30 m/s João demora 2 min para chegar à escola. Se andar a 12 m/s, quanto tempo ele levará para completar o percurso?

Escrevendo as proporções

$numerador 30 espaço reto m dividido por reto s sobre denominador 12 espaço reto m dividido por reto s fim da fração igual a numerador 2 espaço min sobre denominador reto x fim da fração$

Como se trata de grandezas inversas, devemos inverter uma razão.

$12 sobre 30 igual a 2 sobre reto x$

Utilizando a propriedade fundamental das proporções, multiplicamos cruzado.

$Error converting from MathML to accessible text.$

Como vimos na tabela do exemplo, se João diminuir a velocidade para 12 m/s, ele aumentará o tempo para 5 min.

Veja também: Proporcionalidade

Exercícios comentados sobre grandezas diretamente e inversamente proporcionais

Questão 1

Classifique as grandezas relacionadas a seguir em diretamente ou inversamente proporcional.

a) Consumo de combustível e quilômetros percorridos por um veículo.
b) Quantidade de tijolos e área de uma parede.
c) Desconto dado em um produto e o valor final pago.
d) Número de torneiras de mesma vazão e tempo para encher uma piscina.

Ver Resposta

Respostas corretas:

a) Grandezas diretamente proporcionais. Quanto mais quilômetros um veículo percorrer, maior o consumo de combustível para realizar o percurso.

b) Grandezas diretamente proporcionais. Quanto maior a área de uma parede, maior o número de tijolos que farão parte dela.

c) Grandezas inversamente proporcionais. Quanto maior o desconto dado na compra de um produto, menor o valor que se pagará pela mercadoria.

d) Grandezas inversamente proporcionais. Se as torneiras possuem a mesma vazão, elas liberam a mesma quantidade de água. Portanto, quanto mais torneiras abertas, menor será o tempo para que a quantidade de água necessária para preencher a piscina seja liberada.

Questão 2

Pedro tem uma piscina em sua casa que mede 6 m de comprimento e comporta 30 000 litros de água. Seu irmão Antônio decide também construir uma piscina com a mesma largura e profundidade, mas com 8 m de comprimento. Quantos litros de água cabem na piscina de Antônio?

a) 10 000 L
b) 20 000 L
c) 30 000 L
d) 40 000 L

Ver Resposta

Resposta correta: d) 40 000 L.

Agrupando as duas grandezas dadas no exemplo, temos:

Grandezas	Pedro	Antônio
Comprimento da piscina (m)	6	8
Volume de água (L)	30 000	x

De acordo com a propriedade fundamental das proporções, na relação entre as grandezas, o produto dos extremos é igual ao produto dos meios e vice-versa.

$tabela linha com célula com reto a sobre reto b fim da célula igual a célula com reto c sobre reto d fim da célula seta dupla para a esquerda e para a direita célula com reto a. reto d fim da célula igual a linha com blank blank blank blank seta para baixo blank fim da tabela tabela linha com célula com reto b. reto c fim da célula blank linha com seta para a direita com gancho célula com Produto espaço dos espaço extremos fim da célula fim da tabela espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço Produto espaço dos espaço meios$

Para resolver essa questão utilizamos o x como incógnita, ou seja, o quarto valor que deve ser calculado a partir dos três valores dados no enunciado.

$Error converting from MathML to accessible text.$

Utilizando a propriedade fundamental das proporções, calculamos o produto dos meios e o produto dos extremos para encontrar o valor de x.

$6 espaço. espaço reto x espaço igual a espaço 8 espaço. espaço 30 espaço 000 espaço espaço espaço 6 reto x espaço igual a espaço espaço 240 espaço 000 espaço espaço espaço espaço espaço reto x espaço igual a espaço numerador 240 espaço 000 sobre denominador 6 fim da fração espaço espaço espaço espaço espaço reto x espaço igual a espaço 40 espaço 000 espaço reto L espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço$

Observe que entre as grandezas há proporcionalidade direta: quanto maior o comprimento da piscina, maior a quantidade de água que ela comporta.

Veja também: Razão e Proporção

Questão 3

Em uma lanchonete, seu Alcides prepara suco de morango todos os dias. Em 10 minutos e utilizando 4 liquidificadores, a lanchonete consegue preparar os sucos que os clientes pedem. Para diminuir o tempo de preparo, seu Alcides dobrou o número de liquidificadores. Quanto tempo levou para que os sucos ficassem prontos com os 8 liquidificadores funcionando?

a) 2 min
b) 3 min
c) 4 min
d) 5 min

Ver Resposta

Resposta correta: d) 5 min.

Liquidificadores

(número)

Tempo

(minutos)

Note que entre as grandezas da questão há proporcionalidade inversa: quanto mais liquidificadores estiverem preparando suco, menos tempo será necessário para que todos estejam prontos.

Sendo assim, para resolver esse problema a grandeza de tempo deve ser invertida.

$tabela linha com célula com 4 sobre 8 fim da célula igual a célula com reto x sobre 10 fim da célula fim da tabela$

Aplicamos então a propriedade fundamental da proporção e resolvemos a questão.

$8. espaço reto x espaço igual a espaço 4 espaço. espaço 10 espaço espaço espaço 8 reto x espaço igual a espaço espaço 40 espaço espaço espaço espaço reto x espaço igual a espaço 40 sobre 8 espaço espaço espaço espaço reto x espaço igual a espaço espaço 5 espaço min$

Não pare por aqui, você também pode se interessar por:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações